İkinci dereceden bir denklem veya ikinci dereceden denklem , terimlerinden birinin en büyük üssünün 2’ye eşit olduğu, 2. derece bir denklemdir. Bu, denklemin en fazla iki farklı çözümü olabileceği anlamına gelir, ancak aynı zamanda benzersiz bir çözümü veya hiç yok.
İkinci dereceden denklemlerin çözümlerini veya köklerini hesaplamak için iki farklı prosedür izleyebiliriz: ikinci dereceden formül aracılığıyla veya ifadeyi çarpanlara ayırarak . Bu yazımızda her iki yöntemden de bahsedeceğiz ve size bazı pratik alıştırmalar vereceğiz. Ancak daha önce bazı kavramları açıklığa kavuşturacağız, böylece tüm açıklama çok iyi anlaşılacak ve okumadan en iyi şekilde yararlanacaksınız.
İkinci Dereceden Denklem Türleri
İkinci dereceden denklemler arasındaki ana sınıflandırma, ifadenin yapısına dayanmaktadır. Dolayısıyla bu ifadelerin standart veya olağan yapısı şu şekildedir: ax² + bx + c . Bu ortak biçim tam bir denkleme eşdeğerdir, ancak boş veya boş terimler olduğunda yapı değişebilir ve bu durumda eksik denklemler ortaya çıkar. Daha sonra tüm türlerin özelliklerini daha ayrıntılı olarak açıklayacağız.
İkinci dereceden denklemleri tamamla
Daha önce de söylediğimiz gibi elimizde tam ikinci dereceden denklemler var, bunların tüm katsayıları a, b ve c sıfırdan farklı. Bu nedenle ifade, tüm terimleri içerdiğinden harfe kadar ax² + bx + c yapısını takip eder: ikinci dereceden terim, doğrusal terim ve bağımsız terim. Bu türün bir örneği aşağıdaki denklemdir: x² + 2x + 1 = 0.
Tamamlanmamış ikinci dereceden denklemler
Eksik denklemlere gelince, onları hangi katsayının sıfıra eşit olduğuna göre ayırt edebiliriz. Unutmayın, eğer bu açıklama şüphelerinizi gidermezse hemen aşağıda tüm vakaların adım adım açıklandığı görseli bulabilirsiniz.
- Tamamlanmamış denklemler (b = 0): Bu ilk durumda aşağıdaki yapıyı takip eden bir ifade buluruz: ax² + c = 0. Bununla iki sonuç elde ederiz: c/a kesirinin kökünün negatifi ve pozitifi .
- Eksik denklemler (c = 0): ax² + bx = 0 formuna sahip olduğumuzda, x (ax + b) = 0 ifadesini elde etmek için denklemi çarpanlara ayırmalıyız. Bu nedenle iki çözümümüz olacaktır: x = 0 ve x = – b/a.
- Eksik denklemler (b = c = 0): bu durumda ax² = 0 denklemimiz var ve yalnızca bir olası çözümümüz var, o da x = 0.
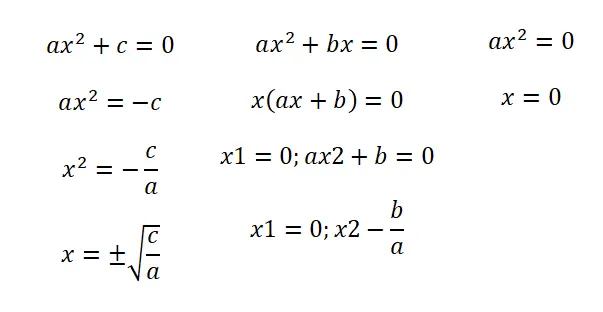
Size öğrettiğimiz prosedürlerin, eksik denklemleri çözerken daha hızlı ilerlemenizi sağladığını belirtmekte fayda var. Ancak her durumda aşağıda size öğreteceğimiz ikinci dereceden formülü kullanabilirsiniz, var olmayan katsayılara yalnızca sıfır yazmanız yeterli olacaktır.
İkinci dereceden denklemler için formül
İkinci dereceden denklemleri (ax² + bx + c = 0) çözmek için genel formülü veya ikinci dereceden formülü uygulamamız ve ardından matematiksel ifadedeki her harfe karşılık gelen sayısal değerleri yerine koymamız gerekir.
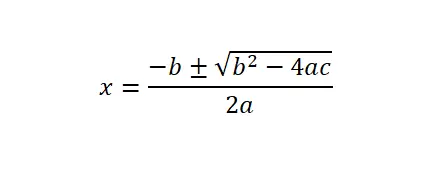
Ayrıca diskriminantın (Δ) karekök altında yer alan b² – 4ac ifadesi olduğunu da açıklamak önemlidir. Bu matematiksel kavramdan, bu ikinci dereceden denklemin kaç çözümü olduğunu bilebiliriz. Temel olarak üç seçenek vardır: Diskriminant negatiftir (gerçek çözüm yoktur), diskriminant sıfırdır (sadece bir çözüm vardır) veya diskriminant pozitiftir (iki çözüm vardır).
Çözülmüş Tam İkinci Dereceden Denklem Örneği
Aşağıdaki ikinci dereceden denklemi çözmeyi deneyin: 2x²+4x-6=0 ve sonucunuzu aşağıdaki denklemle kontrol edin. Aşağıdaki prosedürü izlemenizi öneririz: denklem türünü analiz edin (sıfır terimleri belirleyin), mevcut çözümlerin sayısını bilmek için diskriminantı hesaplayın ve son olarak önerilen denklemi formülle çözün.
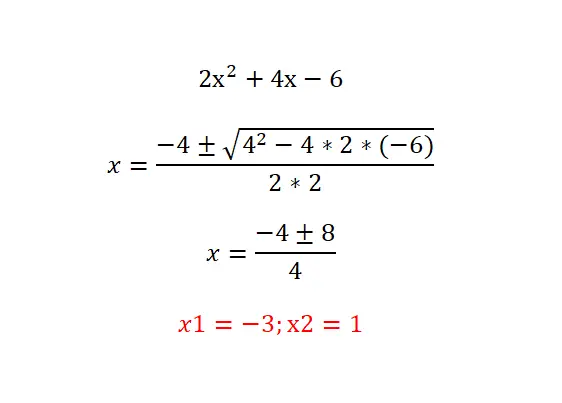
Faktöriyel ikinci dereceden denklemler
İkinci dereceden denklemleri çözmek için kullandığımız ikinci yöntem çarpanlara ayırmadır . Dolayısıyla,bir polinomu (bizim durumumuzda ikinci dereceden bir polinom) çarpanlara ayırmak için farklı yöntemler kullanabiliriz. Genel olarak, bu tarzdaki denklemler söz konusu olduğunda, bunlar genellikle ortak bir terimle çarpanlara ayrılabilir. Değilse, Notable Identities’i uygulamayı deneyebilirsiniz, ancak normalde bu durumlarda başka herhangi bir yöntem bilmenize gerek yoktur.
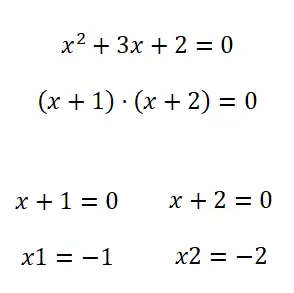
Çözümlü ikinci dereceden denklem alıştırmaları
Aşağıda tam ve eksik ikinci dereceden denklemlerle ilgili bir dizi alıştırma bulacaksınız. Bu şekilde, bu makale boyunca açıklanan tüm teoriyi gözden geçirecek ve bunu alıştırmalarda nasıl uygulayacağınızı daha net anlayacaksınız. Bunları kendi başınıza çözmeye çalışmanızı ve çözüme yalnızca tamamladığınızda veya takılıp kaldığınızda bakmanızı öneririz. Bununla birlikte, şimdi alıştırmaları çözmeye başlayabilirsiniz.
1. Egzersiz
Aşağıdaki ikinci dereceden denklemi çözün:
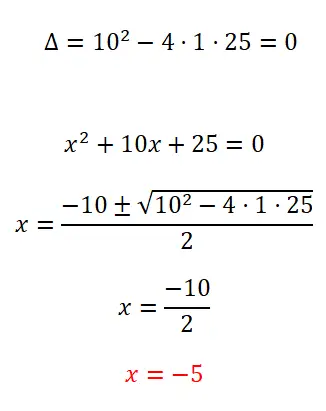
- Olası çözümlerin sayısını bilmek için diskriminantı hesaplayarak başlıyoruz.
- Bu tam ikinci dereceden bir denklem olduğu için ikinci dereceden formülü uygulayıp hesaplamaları çözüyoruz.
- Bilinmeyen x’in değerini elde ederiz.
Alıştırma 2
Aşağıdaki ikinci dereceden denklemi çözün:
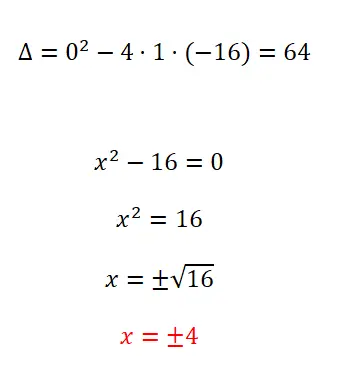
- Diskriminant değerini hesaplayarak başlıyoruz.
- B = 0 olan ikinci dereceden tamamlanmamış bir denklemimiz olduğundan, bu tür denklemler için standardı uyguluyoruz.
- Sonucu elde etmek için hesaplamayı çözüyoruz ve ± işaretini unutamıyoruz.
Alıştırma 3
Aşağıdaki sırasız ikinci dereceden denklemi çözün:
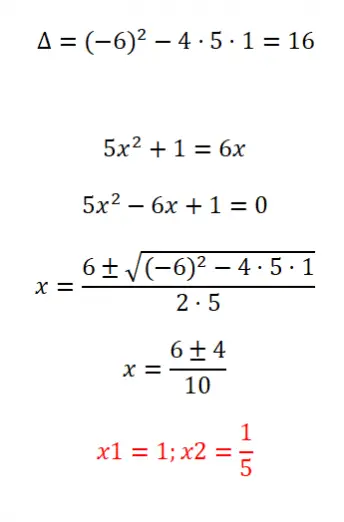
- Denklemin diskriminantını hesaplayarak başlıyoruz.
- Formülü uygulayabilmemiz için önce denklemi ax² + bx + c = 0 yapısına göre sıralamamız gerekiyor.
- Daha sonra genel formülü uyguluyoruz.
- Ve sonunda sonuçlara ulaşıyoruz.
Alıştırma 4
Aşağıdaki ikinci dereceden denklemi çarpanlarına ayırarak çözün:
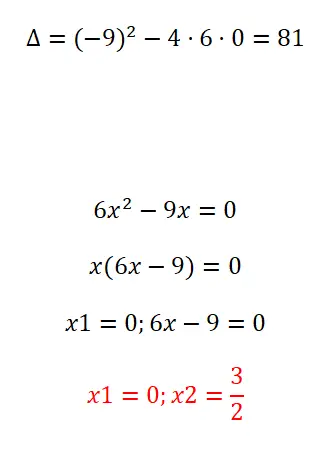
- İlk önce diskriminantı hesaplıyoruz.
- Daha sonra x’in ortak faktörünü çıkarıyoruz.
- Yani ilk çözüm x = 0’dır.
- İkincisi ise x = 3/2.
Alıştırma 5
Aşağıda gösterdiğimiz ikinci dereceden denklemin tamamını çözün:
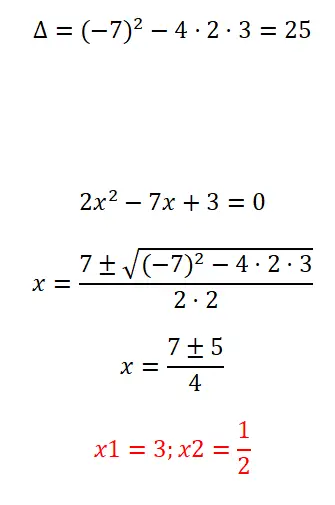
- Her zaman olduğu gibi söz konusu denklemin kaç çözümü olduğunu bulmak için diskriminantı hesaplıyoruz.
- Daha sonra, tam bir denklem olduğu için ikinci dereceden formülü uyguluyoruz.
- Son olarak denklemin sonucunu ifade ediyoruz.
Alıştırma 6
İkinci dereceden denklemi sunduğumuz kesirlerle çözün:
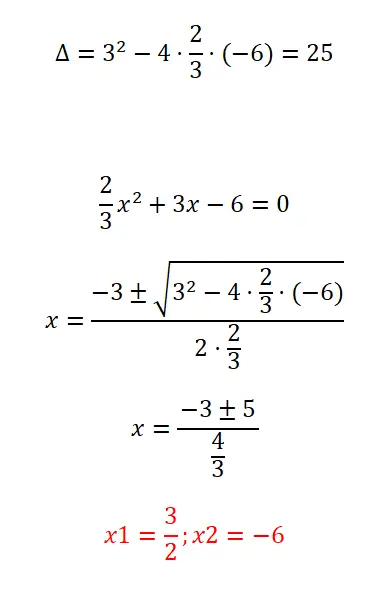
- İfadenin diskriminantını hesaplayarak başlıyoruz.
- Daha sonra, “a” katsayısının bir kesirden oluştuğunu dikkate alarak ikinci dereceden formülü uyguluyoruz.
- Hesaplamayı çözüyoruz.
- Ve elimizde zaten denklemin iki kökü var.
Egzersiz 7
Aşağıdaki ikinci dereceden denklemi çözün:
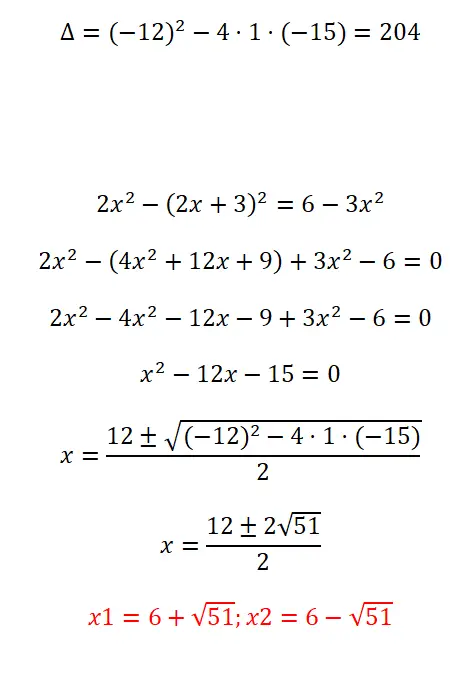
- Diskriminant değerini hesaplayarak başlıyoruz.
- Formülü uygulamadan önce ifadeyi sadeleştirip ax² + b + c = 0 formunu vermemiz gerekiyor.
- Formüldeki tüm katsayıları yerine koyup hesaplamayı çözüyoruz.
- Sonunda sonuca ulaşıyoruz.
Egzersiz 8
Aşağıdaki ikinci dereceden denklemin çözümünün kanıtı:
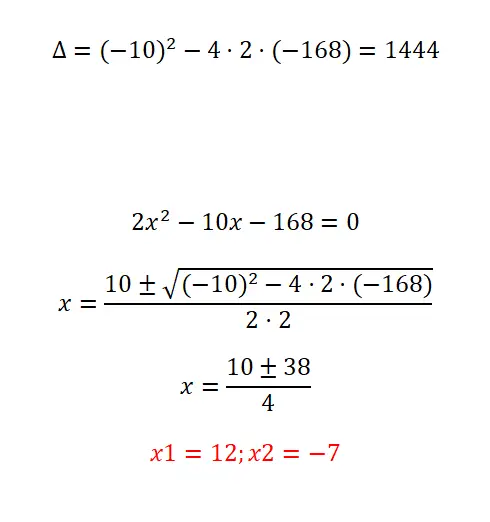
- Diskriminant değerini hesaplayarak başlıyoruz.
- Gördüğünüz gibi, oldukça büyük katsayılara sahip olmasına rağmen bu basit bir ikinci dereceden denklemdir. Bu nedenle işlemleri yaparken formülü uygulamamız ve dikkatli olmamız gerekiyor.
- Sonunda her iki olası çözümü de elde ederiz.