▷ İki vektörün çapraz çarpımını hesaplayın (örnekler)

Bu sayfada iki vektörün çapraz çarpımının ne olduğu ve nasıl hesaplandığı açıklanmaktadır. Ayrıca sağ el kuralını (veya tirbuşonu) kullanarak çapraz çarpımın yönünü ve yönünü nasıl bulacağınızı da göreceksiniz. Dahası, bu tür işlemlerin kullanımlarının yanı sıra örnekler, alıştırmalar ve adım adım çözülen problemler de bulacaksınız.

İki vektörün çapraz çarpımı nedir?

Matematikte çapraz çarpım , üç boyutlu uzayda (R3’te) iki vektör arasındaki bir işlemdir. Bu vektör işleminin sonucu, çarpılan iki vektöre dik yönde ve çarpan vektörlerinin modüllerinin, oluşturdukları açının sinüsüne eşit bir modüle sahip bir vektördür. Başka bir deyişle formülü şu şekildedir:

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha)$

Önceki formülde gördüğünüz gibi çapraz çarpım gösterilir

$\bm{\times}$

bu yüzden buna çapraz çarpım da denir. Gibbs’in icat etmesinden dolayı bazen Gibbs vektör çarpımı olarak da anılır.

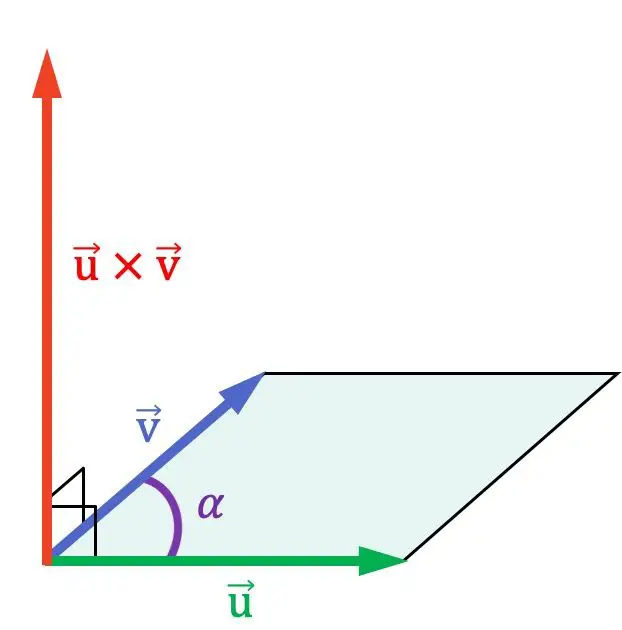
Önceki grafik gösterimde görebileceğiniz gibi, çapraz çarpım çarpıldıkları iki vektöre diktir ve dolayısıyla onları içeren düzleme normaldir.

İki vektörün çapraz çarpımını hesaplamak için formül

Vektörlerin Kartezyen koordinatlarını biliyorsak, çapraz çarpımlarını hesaplamanın en basit yolu 3×3 determinantını çözmektir. Nasıl yapıldığını izleyin:

Herhangi iki vektörü düşünün:

$\vv{\text{u}}= (\text{u}_x,\text{u}_y,\text{u}_z) \qquad \vv{\text{v}}= (\text{v}_x,\text{v}_y,\text{v}_z)$

Vektör çarpımı:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] \text{u}_x & \text{u}_y & \text{u}_z \\[1.1ex] \text{v}_x &\text{v}_y&\text{v}_z \end{vmatrix}$

Vektörler nerede

$\vv{i}, \vv{j},\vv{k}$

Bunlar sırasıyla X, Y ve Z ekseni yönlerindeki birim vektörlerdir.

İki vektör arasındaki çapraz çarpımın nasıl hesaplanacağına dair bir örnek görelim:

$\vv{\text{u}}= (3,1,0) \qquad \vv{\text{v}}= (2,1,-1)$

Vektörler arasındaki vektör çarpımını belirlemek için 3. dereceden aşağıdaki determinantı yapmamız gerekir:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix}$

Bu durumda determinantı adjuvanlar veya kofaktörlerle çözeceğiz (Sarrus kuralı da kullanılabilir):

$\begin{aligned} \vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& 1 & 0 \\[1.1ex] 2 &1&-1 \end{vmatrix} & = \vv{i}\begin{vmatrix} 1 & 0 \\[1.1ex] 1&-1 \end{vmatrix} -\vv{j}\begin{vmatrix} 3& 0 \\[1.1ex] 2 &-1 \end{vmatrix}+\vv{z}\begin{vmatrix}3& 1 \\[1.1ex] 2 &1 \end{vmatrix} \\[2ex] & = -\vv{i}+3\vv{j}+\vv{z}\end{aligned}$

Dolayısıyla iki vektörün vektör çarpımının sonucu şu şekildedir:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-1,3,1)}$

Çapraz çarpımın yönünü ve yönünü belirler

Bazen çapraz çarpımdan elde edilen vektörün bileşenlerini bilmemize gerek kalmaz ama modülünü, yönünü ve yönünü bulmak yeterlidir. Bu genellikle fizikte, özellikle de kuvvetlerin hesaplanmasında olur.

Bu nedenle, vektör çarpımının yönünü ve yönünü bulmak için çeşitli kurallar vardır; en iyi bilinenleri, üç parmakla veya tüm el ile sağ el kuralı ve tirbuşon kuralıdır (veya vida) . Bunlardan herhangi birini kullanabilirsiniz, yani hepsini bilmenize gerek yok, yine de size üç kuralı açıklayacağız, böylece en sevdiğiniz kurala sadık kalabilirsiniz. 😉

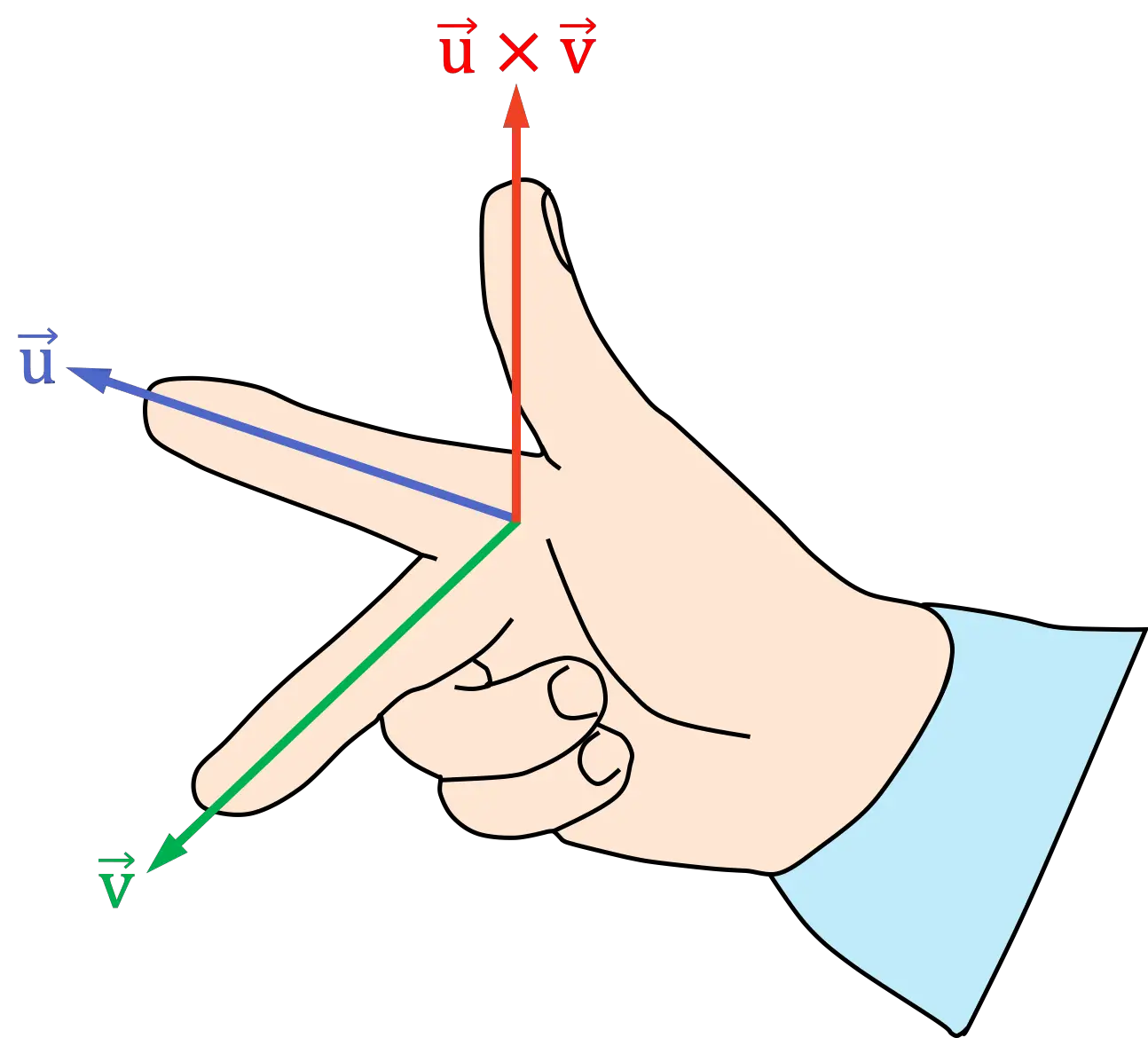
Sağ el kuralı (3 parmak)

Sağ el kuralının veya yasasının 3 parmak versiyonu aşağıdaki adımların gerçekleştirilmesini içerir:

Sağ elinizin işaret parmağını çapraz çarpımın ilk vektörüne doğru yerleştirin
$(\vv{\text{u}}).$
Sağ elinizin orta parmağını (veya orta parmağını) çapraz çarpımın ikinci vektörüne doğru yerleştirin
$(\vv{\text{v}}).$
Ortaya çıkan başparmak konumu çapraz çarpımın yönünü ve yönünü gösterir
$(\vv{\text{u}}\times\vv{\text{v}}).$

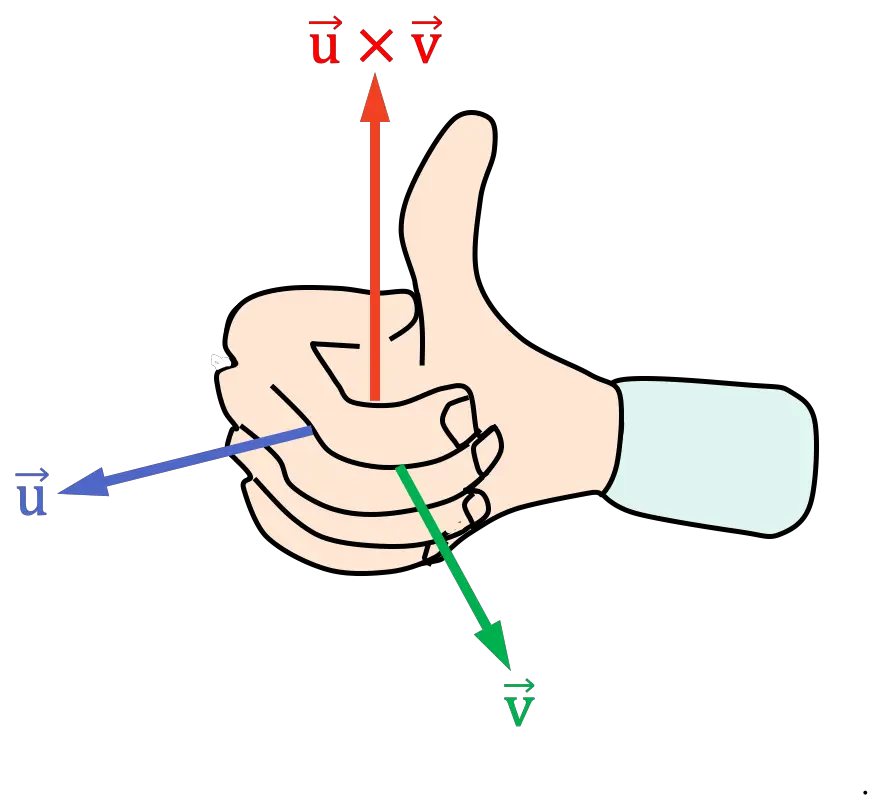
Sağ el kuralı (avuç içi)

Sağ el kuralının veya yasasının palmar versiyonu önceki kurala çok benzer. Uygulamak için aşağıdaki adımları izlemelisiniz:

Sağ elinizi parmaklarınızla çapraz çarpımın ilk vektörüyle aynı yönü gösterecek şekilde koyun
$(\vv{\text{u}}).$
Parmaklarınızı çapraz çarpımın ikinci vektörüne doğru hareket ettirerek sağ elinizi kapatın
$(\vv{\text{v}}).$

Vektörler arasındaki açının (veya mesafenin) daha küçük olduğu tarafta elinizi kapatmanız gerekir.
Başparmağın ortaya çıkan konumu çapraz çarpımın yönünü belirler
$(\vv{\text{u}}\times\vv{\text{v}}).$

tirbuşon kuralı

Tirbuşon veya vida kuralı, avucun tamamını kullanan sağ el kuralına benzer. Prosedür aşağıdaki gibidir:

Hayal gücünüzü kullanarak, sapı çapraz çarpımın ilk vektörüyle aynı yönü gösterecek şekilde bir tirbuşon (veya vida) yerleştirin.
$(\vv{\text{u}}).$
Daha sonra tirbuşonu çapraz çarpımın ikinci vektörüne doğru çevirin
$(\vv{\text{v}})$

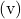
sanki onu bir mantarın içine koyacakmışsın gibi. Tirbuşonu vektörler arasındaki mesafenin en kısa olduğu tarafa çevirmeniz gerekiyor.
Tirbuşon spiral noktalarının yönü vektör çarpımının yönü ve yönü olacaktır.
$(\vv{\text{u}}\times\vv{\text{v}}).$

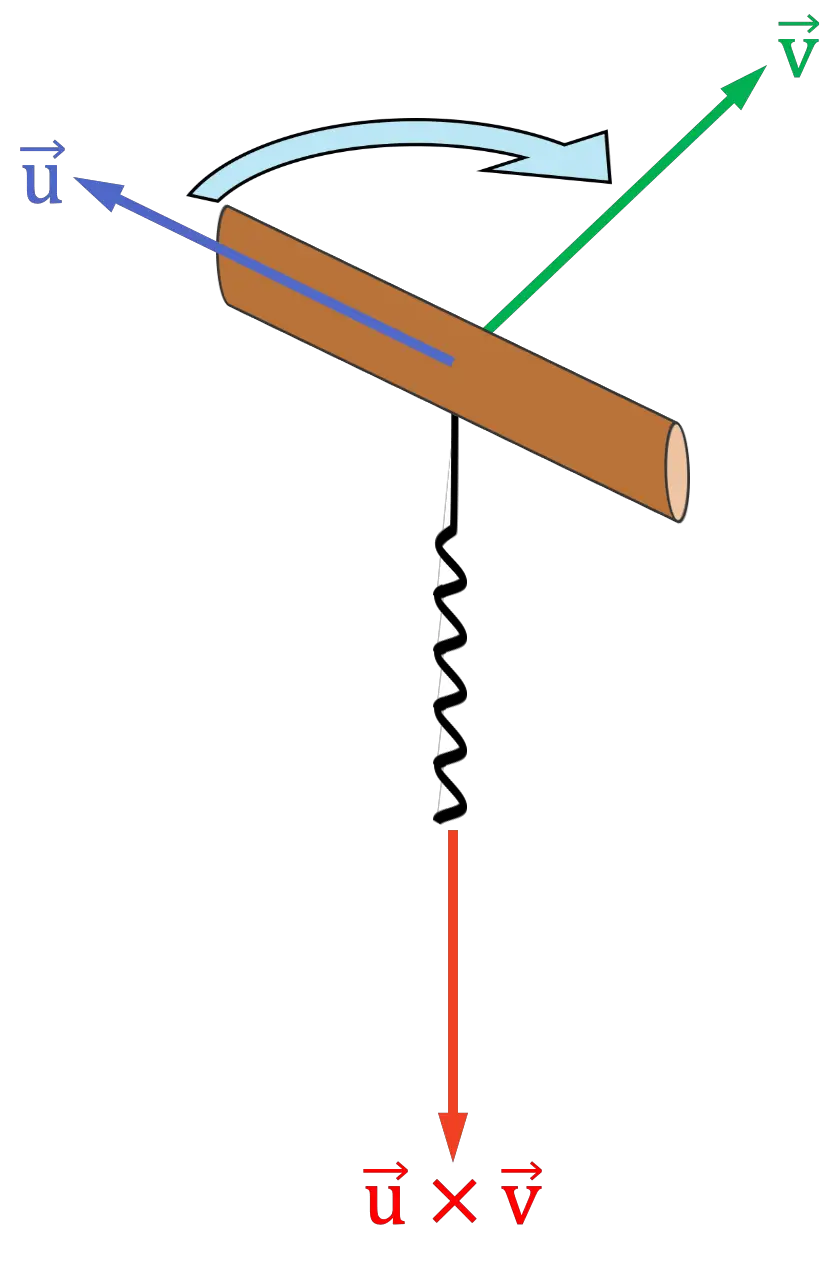
İki vektörün çapraz çarpımının özellikleri

İki vektörün çapraz çarpımı aşağıdaki özelliklere sahiptir:

Anti-değişme özelliği: Vektör çarpımında yer alan vektörlerin sırası kayıtsız değildir çünkü işaret buna göre değişir.

$\vv{\text{u}}\times\vv{\text{v}} = - \vv{\text{v}}\times\vv{\text{u}}$

Vektörlerin toplanması ve çıkarılmasıyla ilgili dağılma özelliği :

$\vv{\text{u}}\times(\vv{\text{v}}+\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}+\vv{\text{u}}\times \vv{\text{w}}$

$\vv{\text{u}}\times(\vv{\text{v}}-\vv{\text{w}}) = \vv{\text{u}}\times\text{v}}-\vv{\text{u}}\times \vv{\text{w}}$

Homojen özellik : Çapraz çarpımın bir vektörünü bir skalerle (gerçek sayı) çarpmak, çapraz çarpımın sonucunu adı geçen skalerle çarpmaya eşdeğerdir.

$k \cdot (\vv{\text{u}}\times\vv{\text{v}}) = (k\cdot \vv{\text{u}})\times\vv{\text{v}}=\vv{\text{u}}\times(k\cdot\vv{\text{v}})$

Vektör çarpımından elde edilen vektör, işlemde yer alan iki vektöre diktir .

$\begin{array}{c} \vv{\text{u}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \\[2ex] \vv{\text{v}} \perp (\vv{\text{u}}\times\vv{\text{v}}) \end{array}$

Ayrıca, iki vektör dik ise aşağıdaki denklemler sağlanır:

$\vv{\text{u}} \perp \vv{\text{v}} \ \longrightarrow \ \begin{cases} \vv{\text{u}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \\[2ex] \vv{\text{v}} \cdot (\vv{\text{u}}\times\vv{\text{v}})=0 \end{array}$

İki paralel vektörün çapraz çarpımı sıfır vektörüne (veya sıfıra) eşittir.

$\vv{\text{u}} \ || \ \vv{\text{v}} \ \longrightarrow \ \vv{\text{u}}\times\vv{\text{v}}=0$

İki vektörün oluşturduğu açıyı bilmiyorsak, vektör çarpımlarının modülü de aşağıdaki ifade kullanılarak hesaplanabilir:

$\lvert \vv{\text{u}}\times\vv{\text{v}} \rvert = \sqrt{ \lvert \vv{\text{u}}\rvert ^2 \cdot \lvert \vv{\text{v}} \rvert ^2 - (\vv{\text{u}}\cdot \vv{\text{v}})^2 \vphantom{\frac{1}{2}}$

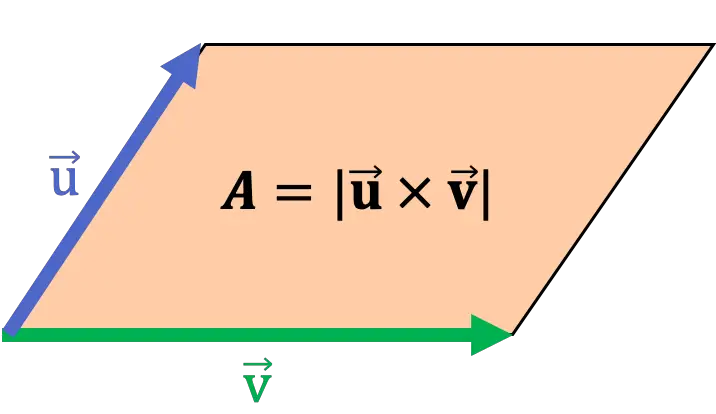
Çapraz çarpımı kullanarak paralelkenarın veya üçgenin alanını hesaplayın

Geometrik olarak, iki vektörün çapraz çarpımının modülü, bu iki vektörün kenar olduğu paralelkenarın alanıyla çakışır. Bu nedenle paralelkenarın alanını hesaplamak için çapraz çarpım kullanılabilir.

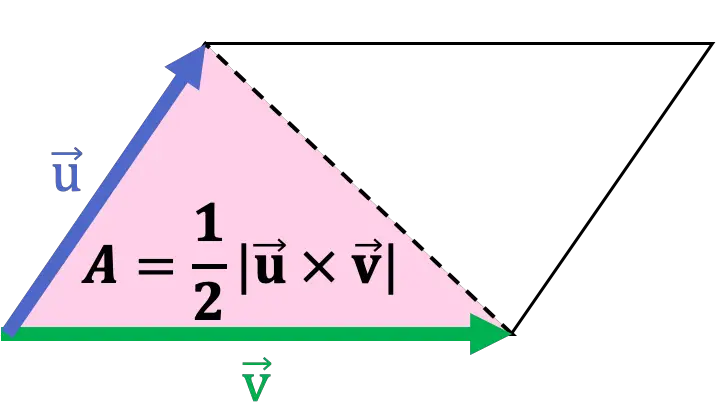
Ayrıca paralelkenarın köşegeni onu iki üçgene böler, başka bir deyişle üçgen paralelkenarın yarısıdır. Böylece bir üçgenin alanı , iki kenarını vektör olarak alan çapraz çarpımın modülünün yarısı kadardır.

3 boyutlu uzaydaki bir vektörün modülünün, koordinatlarının karelerinin toplamının kökü olduğunu hatırlayın:

$\lvert \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} \text{v}_x^2+\text{v}_y^2+\text{v}_z^2}$

Bunlar iki vektörün çapraz çarpımının matematik alanındaki uygulamalarından ikisidir. Ancak yine de başka kullanımları da vardır; örneğin fizikte manyetik alanı hesaplamak için kullanılır.

Vektörlerin vektör çarpımlarına ilişkin çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki iki vektör arasındaki çapraz çarpımı hesaplayın:

$\vv{\text{u}}= (-1,4,2) \qquad \vv{\text{v}}= (0,-2,1)$

Çözümü görün

Vektörler arasındaki vektör çarpımını belirlemek için aşağıdaki 3×3 boyutunun determinantını çözmemiz gerekir:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1 \end{vmatrix}$

Bu durumda determinantı adjuvanlar veya kofaktörlerle çözeceğiz (ancak Sarrus kuralı da kullanılabilir):

$\begin{aligned}\begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] -1& 4 & 2 \\[1.1ex] 0 &-2&1\end{vmatrix} & = \vv{i}\begin{vmatrix} 4 & 2 \\[1.1ex]-2&1\end{vmatrix} -\vv{j}\begin{vmatrix} -1& 2 \\[1.1ex] 0 &1\end{vmatrix}+\vv{z}\begin{vmatrix}-1& 4 \\[1.1ex] 0 &-2\end{vmatrix} \\[2ex] & = 8\vv{i}+\vv{j}+2\vv{z}\end{aligned}$

Dolayısıyla iki vektörün vektör çarpımının sonucu şu şekildedir:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(8,1,2)}$

Alıştırma 2

Aşağıdaki iki vektör arasındaki çapraz çarpımı bulun:

$\vv{\text{u}}= (3,-2,4) \qquad \vv{\text{v}}= (1,5,-3)$

Çözümü görün

İki vektör arasındaki vektör çarpımını bulmak için aşağıdaki 3×3 determinantı çözmemiz gerekir:

$\vv{\text{u}} \times \vv{\text{v}}=\begin{vmatrix} \vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3 \end{vmatrix}$

Bu durumda, determinantı eklerle veya kofaktörlerle çözeceğiz (her ne kadar Sarrus kuralı birbirinin yerine kullanılabilirse de):

$\begin{aligned} \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex] 3& -2 & 4 \\[1.1ex] 1 &5&-3\end{vmatrix} & = \vv{i}\begin{vmatrix} -2 & 4 \\[1.1ex] 5&-3\end{vmatrix} -\vv{j}\begin{vmatrix} 3& 4 \\[1.1ex] 1&-3\end{vmatrix}+\vv{z}\begin{vmatrix}3& -2 \\[1.1ex] 1 &5\end{vmatrix} \\[2ex] & = -14\vv{i}+13\vv{j}+17\vv{z}\end{aligned}$

Dolayısıyla iki vektör arasındaki vektör çarpımının sonucu şu şekildedir:

$\vv{\text{u}} \times \vv{\text{v}}=\bm{(-14,13,17)}$

Alıştırma 3

İki vektörün modüllerini ve oluşturdukları açıyı bilmek:

$|\vv{\text{u}}|= 5 \qquad |\vv{\text{v}}|= 6 \qquad \alpha = 30º$

İki vektörün çapraz çarpımının büyüklüğünü belirleyin.

Çözümü görün

Aşağıdaki formülü uygulayarak iki vektör arasındaki vektör çarpımının modülünü kolayca hesaplayabiliriz:

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 5 \cdot 6 \cdot \text{sen}(30º) \\[2ex] &= 30 \cdot 0,5 \\[2ex] &= \bm{15} \end{aligned}$

Alıştırma 4

Ekran düzleminde bulunan aşağıdaki vektörlerden:

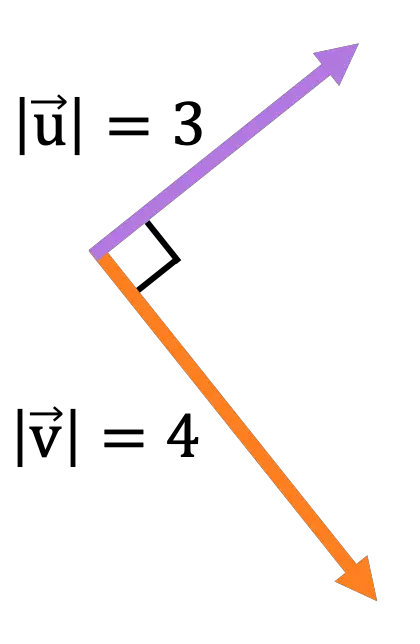
doğrultudaki iki vektörün çapraz çarpımı

Aşağıdaki vektör işleminden elde edilen vektörün büyüklüğünü, yönünü ve yönünü hesaplayın:

$\lvert \vv{\text{u}} \times \vv{\text{v}}\rvert$

Çözümü görün

İki vektör birbirine dik olduğundan vektör çarpımının normu şöyle olacaktır:

$\begin{aligned} \lvert \vv{\text{u}} \times \vv{\text{v}}\rvert & = \lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}}\rvert \cdot \text{sen}(\alpha) \\[2ex] & = 3 \cdot 4 \cdot \text{sen}(90º) \\[2ex] &= 12 \cdot 1 \\[2ex] &= \bm{12} \end{aligned}$

Öte yandan, vektör çarpımından elde edilen vektör, işleme katılan iki vektöre dik olduğundan yönü ekrana dik olacaktır.

Ve son olarak, düz çizgi (veya tirbuşon) kuralını kullanarak, ortaya çıkan vektörün yönünün ekranın iç kısmına doğru olacağı sonucunu çıkarabiliriz.

Alıştırma 5

İki tarafı aşağıdaki vektörlere sahip olan paralelkenarın alanını hesaplayın:

$\vv{\text{u}}= (2,3,-2) \qquad \vv{\text{v}}= (5,0,-1)$

Çözümü görün

Bir paralelkenarın alanı, onu oluşturan vektörlerin çapraz çarpımının modülü ile çakışmaktadır. Bu nedenle vektörlerin vektör çarpımını hesaplıyoruz:

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& 3 & -2 \\[1.1ex] 5 &0&-1\end{vmatrix} & = \vv{i}\begin{vmatrix} 3 & -2 \\[1.1ex] 0&-1\end{vmatrix} -\vv{j}\begin{vmatrix} 2& -2 \\[1.1ex] 5 &-1\end{vmatrix}+\vv{z}\begin{vmatrix}2& 3 \\[1.1ex] 5 &0\end{vmatrix} \\[2ex] & = -3\vv{i}-8\vv{j}-15\vv{z}\end{aligned}$

Ve sonra modülünüz:

$A=\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-3)^2+(-8)^2+(-15)^2}=\bm{17,26} \ \mathbf{u}\bm{^2}$

Alıştırma 6

Köşeleri aşağıdaki noktalar olan üçgenin alanını bulun:

$A(2,1,0) \qquad B(4,0,3)\qquad C(-1,2,3)$

Çözümü görün

Öncelikle üçgenin kenarlarını oluşturan vektörleri hesaplamamız gerekiyor:

$\vv{AB} = B- A = (4,0,3)-(2,1,0) = (2,-1,3)$

$\vv{BC} =C- B =(-1,2,3)- (4,0,3) = (-5,2,0)$

Bir üçgenin alanı, onu oluşturan vektörlerin vektör çarpımının büyüklüğünün yarısı kadardır. Bu nedenle vektörlerin vektör çarpımını hesaplıyoruz:

$\begin{aligned} \vv{\text{u}}\times \vv{\text{v}} = \begin{vmatrix}\vv{i}& \vv{j}& \vv{k} \\[1.1ex]2& -1 & 3 \\[1.1ex] -5 &2&0\end{vmatrix} & = \vv{i}\begin{vmatrix} -1 & 3 \\[1.1ex] 2&0\end{vmatrix} -\vv{j}\begin{vmatrix} 2& 3 \\[1.1ex] -5 &0\end{vmatrix}+\vv{z}\begin{vmatrix}2& -1 \\[1.1ex] -5 &2\end{vmatrix} \\[2ex] & = -6\vv{i}-15\vv{j}-\vv{z}\end{aligned}$

Modülünüzden sonra:

$\lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \sqrt{\vphantom{\frac{1}{2}} (-6)^2+(-15)^2+(-1)^2}=16,19$

Ve son olarak üçgenin alanı modülün yarısı olacaktır:

$A=\cfrac{1}{2}\cdot \lvert\vv{\text{u}}\times \vv{\text{v}} \rvert = \cfrac{1}{2}\cdot 16,19=\bm{8,09} \ \mathbf{u}\bm{^2}$

İki vektörün çapraz çarpımı (veya çapraz çarpımı)

İki vektörün çapraz çarpımı nedir?

İki vektörün çapraz çarpımını hesaplamak için formül

Çapraz çarpımın yönünü ve yönünü belirler

Sağ el kuralı (3 parmak)

Sağ el kuralı (avuç içi)

tirbuşon kuralı

İki vektörün çapraz çarpımının özellikleri

Çapraz çarpımı kullanarak paralelkenarın veya üçgenin alanını hesaplayın

Vektörlerin vektör çarpımlarına ilişkin çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Alıştırma 6

Yorum bırakın Yanıtı iptal et