İki nokta arasındaki mesafe formülü (geometri)

Bu sayfada geometride (formül) iki nokta arasındaki mesafenin nasıl hesaplanacağını bulacaksınız. Ayrıca örnekleri görebilecek ve ayrıca iki nokta arasındaki mesafeye ilişkin çözümlü alıştırmalar yapabileceksiniz.

İki nokta arasındaki mesafenin formülü nedir?

İki nokta arasındaki mesafe onları birleştiren doğru parçasının uzunluğuna eşittir. Bu nedenle matematikte iki farklı nokta arasındaki mesafeyi belirlemek için koordinatları arasındaki farkların karelerini hesaplamalı ve daha sonra bu karelerin toplamının kökünü bulmalıyız.

Yani Kartezyen düzlemde iki farklı nokta arasındaki mesafeyi hesaplamak için kullanılan formül şu şekildedir:

İki farklı noktanın koordinatlarını düşünün:

$A(x_1,y_1) \qquad \qquad B(x_2,y_2)$

İki nokta arasındaki mesafenin formülü :

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Bu formül bir vektörün büyüklüğünden gelir. Aslında bu formülle yaptığımız aslında söz konusu iki noktanın belirlediği vektörün büyüklüğünü hesaplamaktır. Bir vektörün modülünün ne olduğuna ilişkin açıklamada bununla ilgili daha fazla bilgi edinebilirsiniz.

Öte yandan analitik geometride iki nokta arasındaki mesafe formülünün gösterimi Pisagor teoremi kullanılarak da yapılabilir:

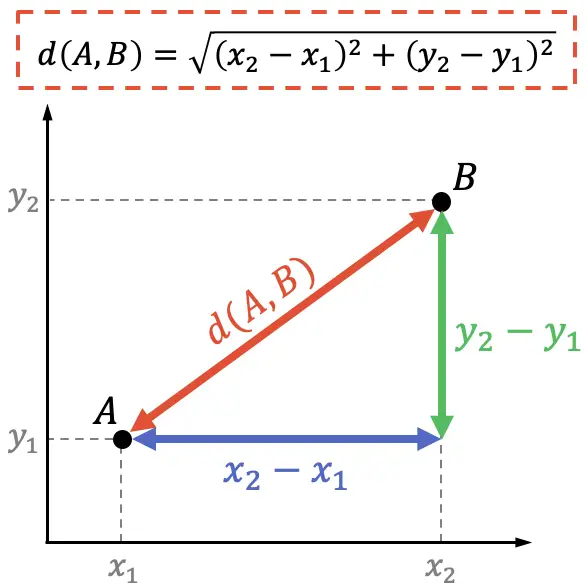
Pisagor teoremi, bir dik üçgenin hipotenüsünün karesinin dik kenarlarının karelerinin toplamına eşdeğer olduğunu belirtir, bu nedenle:

$\bigl(d(A,B)\bigr)^2 = (x_2-x_1)^2 + (y_2-y_1)^2$

Formülü elde etmek için 2 nokta arasındaki mesafeyi bulmanız yeterlidir:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Son olarak, eğer 3 koordinatlı noktalarla çalışıyor olsaydık, uzaydaki (R3’teki) iki nokta arasındaki mesafe formülünün aynı olacağını ancak Z koordinatını ekleyeceğini belirtmekte fayda var:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2 \vphantom{\frac{1}{2}}}$

İki nokta arasındaki mesafeyi hesaplama örneği

İki nokta arasındaki mesafe formülünün tanımını gördükten sonra, şimdi bir örnekle söz konusu mesafenin nasıl belirleneceğini görelim:

Aşağıdaki iki nokta arasındaki mesafeyi bulun:

$A(-1,7) \qquad \qquad B(3,4)$

İki nokta arasındaki mesafeyi geometrik olarak bulmak için aşağıdaki formülü uygulamanız yeterlidir:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Şimdi noktaların koordinatlarını formülde değiştiriyoruz:

$d(A,B) = \sqrt{(3-(-1))^2+(4-7)^2 \vphantom{\frac{1}{2}}}$

Ve hesaplamaları yapıyoruz:

$\begin{aligned} d(A,B) &= \sqrt{(3+1)^2+(4-7)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{4^2+(-3)^2 \vphantom{\frac{1}{2}}} \\[2ex] &= \sqrt{16+9}\\[2ex] &= \sqrt{25}\\[2ex] & = \bm{5}\end{aligned}$

Bu nedenle iki nokta arasındaki mesafe 5 birime eşittir.

Açıkçası mesafe değeri bize her zaman pozitif bir işaret vermelidir çünkü mesafeler her zaman pozitiftir. Aksi takdirde bir adımda hata yapmışız demektir.

İki nokta arasındaki mesafeyi giderme

1. Egzersiz

Aşağıdaki iki nokta arasındaki mesafeyi hesaplayın:

$A(4,2) \qquad \qquad B(1,5)$

Çözüme bakın

İki nokta arasındaki geometrik uzaklığı bulmak için aşağıdaki formülü kullanmanız yeterlidir:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Şimdi noktaların koordinatlarını formülde değiştiriyoruz:

$d(A,B) = \sqrt{(1-4)^2+(5-2)^2 \vphantom{\frac{1}{2}}}$

Ve hesaplamaları yapıyoruz:

$\begin{aligned} d(A,B) & = \sqrt{(-3)^2+3^2 } \\[2ex] & = \sqrt{9+9 } \\[2ex] & = \bm{\sqrt{18}} \end{aligned}$

Alıştırma 2

Aşağıdaki iki nokta arasındaki mesafeyi bulun:

$A(8,6) \qquad \qquad B(-4,1)$

Çözüme bakın

İki nokta arasındaki matematiksel mesafeyi bulmak için ilgili formülü kullanmalıyız:

$d(A,B) = \sqrt{(x_2-x_1)^2+(y_2-y_1)^2 \vphantom{\frac{1}{2}}}$

Şimdi noktaların koordinatlarını formülde değiştiriyoruz:

$d(A,B) = \sqrt{(-4-8)^2+(1-6)^2 \vphantom{\frac{1}{2}}}$

Ve hesaplamaları yapıyoruz:

$\begin{aligned} d(A,B) &= \sqrt{(-12)^2+(-5)^2 } \\[2ex] &= \sqrt{144+25 }\\[2ex] &= \sqrt{169} \\[2ex] &= \bm{13}\end{aligned}$

Alıştırma 3

Aşağıda grafiksel olarak gösterilen A, B ve C noktalarının oluşturduğu üçgenin çevresini hesaplayın:

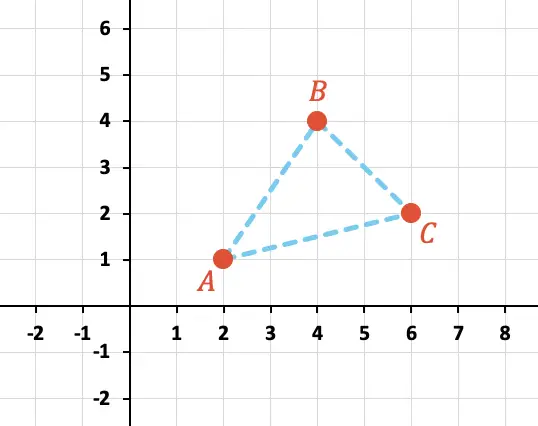
iki nokta arasındaki mesafenin çözümlü alıştırması

Çözüme bakın

Öncelikle grafikteki her noktanın X ve Y koordinatlarını tanımlamamız gerekiyor:

$A(2,1)$

$B(4,4)$

$C(6,2)$

Şimdi tüm noktalar arasındaki mesafeyi aşağıdaki formülle hesaplamamız gerekiyor:

$d(A,B) = \sqrt{(4-2)^2+(4-1)^2 } = \sqrt{4+9} =\sqrt{13} = 3,61$

$d(A,C) = \sqrt{(6-2)^2+(2-1)^2 } = \sqrt{16+1} =\sqrt{17} = 4,12$

$d(B,C) = \sqrt{(6-4)^2+(2-4)^2 } = \sqrt{4+4} =\sqrt{8} = 2,83$

Yani üçgenin çevresi 3 kenar uzunluğunun toplamı olacaktır:

$P=3,61+4,12+2,83= \bm{10,56}$

Alıştırma 4

Köşeleri A, B ve C noktaları olan üçgenin ikizkenar üçgen olup olmadığını kontrol edin. Ama üç nokta:

$A(-4,5) \qquad B(7,-5) \qquad C(10,0)$

Çözüme bakın

Bir üçgenin ikizkenar olması için iki kenarının eşit olması gerekir. Bu nedenle, köşeleri arasındaki mesafelere karşılık gelen her bir kenarının uzunluğunu bulmamız gerekir.

Bu nedenle üçgenin köşeleri arasındaki mesafeyi hesaplıyoruz:

$d(A,B) = \sqrt{(7-(-4))^2+(-5-5)^2 } = \sqrt{11^2+(-10)^2} = \sqrt{221}$

$d(A,C) = \sqrt{(10-(-4))^2+(0-5)^2 } = \sqrt{14^2+(-5)^2} = \sqrt{221}$

$d(B,C) = \sqrt{(10-7)^2+(0-(-5))^2} = \sqrt{3^2+5^2} = \sqrt{34}$

Yani üçgenin 2 özdeş kenarı vardır ve üçüncü kenar diğer ikisinden farklı ölçülür, o zaman bu aslında bir ikizkenar üçgendir.

Alıştırma 5

Y ekseni üzerinde aşağıdaki iki noktadan eşit uzaklıkta olan bir nokta bulun:

$A(5,-3) \qquad \qquad B(-2,4)$

Çözüme bakın

Öncelikle nokta bilgisayar ekseninde (OY ekseni) yer alıyorsa bu, noktanın apsisinin sıfır olduğu anlamına gelir:

$P(0,y)$

İkincisi, eğer nokta A ve B noktalarından eşit uzaklıkta ise bu, aşağıdaki denklemin sağlandığı anlamına gelir:

$d(P,A)= d(P,B)$

Böylece, iki nokta arasındaki mesafe formülünü kullanarak önceki denklemden y değişkeninin değerini bulabiliriz:

$\sqrt{(5-0)^2+(-3-y)^2 \vphantom{\frac{1}{2}}}=\sqrt{(-2-0)^2+(4-y)^2 \vphantom{\frac{1}{2}}}$

Denklemin her iki tarafının da kökü olduğundan bunları basitleştirebiliriz:

$5^2+(-3-y)^2=(-2)^2+(4-y)^2$

Dikkate değer güçleri ve eşitlikleri (veya dikkate değer ürünleri) çözüyoruz:

$25+9+y^2+6y=4+16+y^2-8y$

Ve bilinmeyen y’nin değerini bulana kadar işlem yaparız:

$y^2+6y-y^2+8y=4+16-25-9$

$14y=-14$

$y=\cfrac{-14}{14}$

$y=-1$

Kısaca problem ifadesinin bize sorduğu nokta şudur:

$\bm{P(0,-1)}$

Bu makaleyi faydalı bulduysanız, muhtemelen bir nokta ile bir çizgi arasındaki mesafeye ilişkin alıştırmalarla da ilgileneceksiniz. Bağlantılı sayfada yalnızca adım adım çözülmüş alıştırmalar değil, aynı zamanda noktalar ve çizgiler arasındaki mesafenin hesaplanmasına ilişkin ayrıntılı bir açıklama, örnekler ve başka bir mesafe türünü belirlemek için bir nokta ile bir çizgi arasındaki mesafeye ilişkin formülün uygulanmasını bulacaksınız. .

İki nokta arasındaki mesafe formülü (geometri)

İki nokta arasındaki mesafenin formülü nedir?

İki nokta arasındaki mesafeyi hesaplama örneği

İki nokta arasındaki mesafeyi giderme

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Yorum bırakın Yanıtı iptal et