İki çizgi arasındaki açı (formül)

Bu sayfada iki doğru arasındaki açının (formül) nasıl hesaplanacağının açıklamasını bulacaksınız. Ayrıca çeşitli örnekleri görebileceksiniz ve ayrıca adım adım çözülen alıştırmalarla pratik yapabileceksiniz.

İki çizgi arasındaki açı nedir?

İki doğru arasındaki açı, bu iki doğru arasındaki en küçük açıdır.

Planda, aralarında oluşturdukları açıya göre dört tür çizgi vardır: Kesişen çizgiler (0° ile 90° arası), dik çizgiler (90°), paralel çizgiler (0°) ve çakışan çizgiler (0°).

Kesişen çizgiler

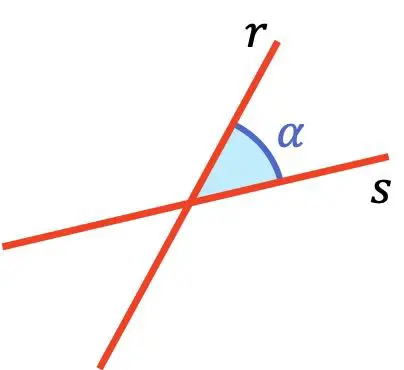
Kesişen çizgiler 0° ile 90° arasında dar bir açıyla kesişir.

Dik düz çizgiler

Dik doğrular 90° dik açıyla kesişir.

Paralel çizgiler

Paralel çizgiler hiçbir zaman birbirine değmez ve aralarında 0° açı yapar.

çakışan çizgiler

İki çakışan doğrunun tüm noktaları ortaktır ve bu nedenle aralarında her zaman 0°’lik bir açı vardır.

Sonuç olarak, iki paralel, çakışan veya dik çizgi arasındaki açının hesaplanması anında yapılır: paralel çizgiler ve çakışan çizgiler aynı yöne sahip oldukları için 0 derecelik bir açı oluştururlar ve dik çizgiler 90 derecelik bir açıyla kesişirler. . Öte yandan kesişen iki çizgi arasındaki açıyı bulmak için bir formül uygulamanız gerekir (bunu aşağıda göreceğiz).

İki çizgi arasındaki açı nasıl hesaplanır?

İki çizgi arasındaki açıyı hesaplamanın iki yolu vardır. Birinci yöntem her çizginin yön vektörünü kullanır, ikinci yöntem ise her çizginin eğimine dayanır.

Her iki prosedür de diğerinden daha iyi değildir, aslında ikisi de oldukça kolaydır, ancak çizgilerin nasıl ifade edildiğine bağlı olarak bir yöntem veya diğeri pratiktir. Bu nedenle her iki matematiksel yöntemi de nasıl kullanacağınızı bilmenizi öneririz.

Çizgi vektör yönlendirme yöntemi

Yön vektörlerini kullanarak iki çizgi arasındaki açıyı hesaplama formülü şöyledir:

İki farklı doğrunun yön vektörleri verildiğinde:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)\qquad \vv{\text{v}} = (\text{v}_x,\text{v}_y)$

Bu iki çizgi arasındaki açı aşağıdaki formülle hesaplanabilir:

$\displaystyle \cos(\alpha) =\cfrac{\lvert \vv{\text{u}} \cdot \vv{\text{v}}\rvert}{\lvert \vv{\text{u}} \rvert \cdot \lvert \vv{\text{v}} \rvert}$

Altın

$\lvert \vv{\text{u}} \rvert$

$\lvert \vv{\text{v}} \rvert$

vektörlerin modülleri

$\vv{\text{u}}$

$\vv{\text{v}}$

sırasıyla.

Bir vektörün büyüklüğünün formülünün şöyle olduğunu unutmayın:

$\displaystyle \lvert \vv{\text{v}} \rvert = \sqrt{ \text{v}_x^2+\text{v}_y^2}$

Bir örnekle iki doğru arasındaki açının nasıl bulunacağını görelim:

Aşağıdaki iki çizgi arasındaki açıyı hesaplayın:

$\displaystyle r: \ \begin{cases} x=2-3t \\[2ex]y=1+4t \end{cases} \qquad s: \ 2x-5y+7=0$

İki çizgi arasındaki açıyı hesaplamak için öncelikle her çizginin yön vektörünü bulmanız gerekir.

doğru

$r$

parametrik bir denklem biçiminde ifade edilir, dolayısıyla vektörün yönünü işaret eden bileşenleri şunlardır:

$\vv{r} = (-3,4)$

ve kanun

$\displaystyle s$

örtülü (veya genel) bir denklem biçiminde tanımlanır, dolayısıyla yön vektörünün koordinatları şöyledir:

$\vv{s} = (-B,A)$

$\vv{s} = (5,2)$

Artık her çizginin yön vektörünü bildiğimize göre iki çizgi arasındaki açı formülünü kullanabiliriz:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Bu nedenle iki vektörün büyüklüğünü belirliyoruz:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-3)^2+4^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{5^2+2^2}= \sqrt{29}$

Açı formülünün vektör işlemlerini gerçekleştiriyoruz:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-3,4) \cdot (5,2)\rvert}{5 \cdot \sqrt{29}}= \cfrac{\lvert-3 \cdot 5 + 4\cdot 2\rvert}{26,93} = \cfrac{7}{26,93} = 0,26$

Ve son olarak, iki çizginin oluşturduğu açıyı kosinüsün tersiyle hesaplıyoruz:

$\alpha= \text{cos}^{-1}(0,26) = \bm{74,93º}$

Hesap makinesini kullanarak kosinüsün tersini hesaplayabileceğinizi unutmayın.

$\boxed{\cos ^{-1}}.$

eğim yöntemi

Açıkçası, bu yöntemi anlamak için çizginin eğimini bilmeniz gerekir. Bu kavramın ne anlama geldiğini, nasıl hesaplandığını, örneklerini ve bir doğrunun eğimi ile ilgili çözümlü alıştırmaları bulabileceğiniz bağlantıda bu kavramı inceleyebilirsiniz.

Eğimlerinden iki çizgi arasındaki açıyı hesaplamak için formül:

Veya iki farklı çizgi:

$r_1 : \ y=m_1 x+n_1 \qquad r_2: \ y=m_2 x+n_2$

Bu iki çizgi arasındaki açı aşağıdaki formülle belirlenebilir:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_2-m_1}{1+m_1\cdot m_2} \end{vmatrix}$

Altın

$m_1$

$m_2$

çizgilerin eğimleri

$r_1$

$r_2$

sırasıyla.

İki doğru arasındaki açının eğimlerini kullanarak nasıl hesaplanacağını bir örnekle görelim:

Aşağıdaki iki çizgi arasındaki açıyı bulun:

$\displaystyle r: \ y=4x-2 \qquad s: \ y=-3x+1$

Her satırın eğimi değişkenden önceki sayıdır

$x:$

$m_r = 4$

$m_s = -3$

Bu nedenle iki çizgi arasındaki açı eğim formülü uygulanarak bulunabilir:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-3-4}{1+4\cdot (-3)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-11} \end{vmatrix} = 0,64$

Ve son olarak teğetin tersiyle olan açıyı buluyoruz:

$\alpha= \text{tg}^{-1}(0,64) = \bm{32,62º}$

Hesap makinesini kullanarak teğetin tersini hesaplayabileceğinizi unutmayın.

$\boxed{\tan ^{-1}}.$

Az önce iki doğrunun eğimlerinin açık bir denklem olarak ifade edildiği bir örnek gördük, ancak bunlar nokta eğim denklemi biçiminde olsaydı aynı prosedürün kullanılması gerekirdi.

İki doğru arasındaki açı problemlerini çözme

1. Egzersiz

Aşağıdaki iki çizginin oluşturduğu açıyı belirleyin:

$\displaystyle r: \ \begin{cases} x=4+t \\[2ex]y=-3-2t \end{cases} \qquad s: \ \begin{cases} x=4t \\[2ex]y=-1-t \end{cases}$

Çözüme bakın

Bu durumda yön vektörü yöntemini kullanacağız. Bu nedenle öncelikle her çizginin yön vektörünü bulmalıyız. Her iki çizgi de parametrik denklemler olarak ifade edilir, dolayısıyla yön vektörlerinin bileşenleri parametrenin önündeki terimlerdir.

$t:$

$\vv{r} = (1,-2)$

$\vv{s} = (4,-1)$

Artık her çizginin yön vektörünü bildiğimize göre iki çizgi arasındaki açı formülünü kullanabiliriz:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Bu nedenle iki vektörün büyüklüğünü belirliyoruz:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{1^2+(-2)^2}= \sqrt{5}$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{4^2+(-1)^2}= \sqrt{17}$

Payın iki vektörü ile paydanın modüllerinin çarpımı arasındaki skaler çarpımı çözüyoruz:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(1,-2) \cdot (4,-1)\rvert}{\sqrt{5} \cdot \sqrt{17}}= \cfrac{\lvert 1 \cdot 4 + (-2)\cdot (-1)\rvert}{9,22} = \cfrac{6}{9,22} = 0,65$

Ve son olarak kosinüsün tersini yaparak iki doğrunun oluşturduğu açıyı buluyoruz:

$\alpha= \text{cos}^{-1}(0,65) = \bm{49,40º}$

Alıştırma 2

Aşağıdaki iki çizgi arasındaki açıyı bulun:

$\displaystyle r: \ -3x+4y+1=0 \qquad s: \ \cfrac{x-1}{6} = \cfrac{y+5}{3}$

Çözüme bakın

Bu problemi yön vektörü yöntemini kullanarak çözeceğiz, bu yüzden önce her çizginin yön vektörünü bulmamız gerekiyor. doğru

$r$

vektörün yönünü işaret eden bileşenleri şöyle olacak şekilde genel (veya örtülü) bir denklem biçiminde ifade edilir:

$\vv{r} = (-B,A)$

$\vv{r} = (-4,-3)$

ve kanun

$\displaystyle s$

sürekli bir denklem biçiminde tanımlanır, dolayısıyla yön vektörünün Kartezyen koordinatları paydaların sayılarıdır:

$\vv{s} = (6,3)$

Her çizginin yön vektörünü öğrendikten sonra iki çizgi arasındaki açı formülünü kullanabiliriz:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

Bu nedenle iki vektörün modüllerini belirliyoruz:

$\displaystyle \lvert \vv{r} \rvert = \sqrt{(-4)^2+(-3)^2}= 5$

$\displaystyle \lvert \vv{s} \rvert = \sqrt{6^2+3^2}= \sqrt{45}$

Açı formülünün vektörleri arasındaki işlemleri gerçekleştiriyoruz:

$\displaystyle \cos(\alpha) =\cfrac{\lvert\vv{r} \cdot \vv{s}\rvert}{\lvert \vv{r} \rvert \cdot \lvert \vv{s} \rvert}$

$\displaystyle \cos(\alpha) =\cfrac{\lvert(-4,-3) \cdot (6,3)\rvert}{5 \cdot \sqrt{45}}= \cfrac{\lvert -4 \cdot 6 + (-3)\cdot 3\rvert}{33,54} = \cfrac{33}{33,54} = 0,98$

Ve son olarak, iki çizginin oluşturduğu açıyı kosinüsün tersiyle hesaplıyoruz:

$\alpha= \text{cos}^{-1}(0,98) = \bm{10,30º}$

Alıştırma 3

Aşağıdaki iki doğru arasındaki açı nedir?

$\displaystyle r: \ y=-2x+9 \qquad s: \ y=5x-1$

Çözüme bakın

Bu durumda çizgiler açık bir denklem biçiminde olduğundan, yaptıkları açıyı bulmak için çizgilerin eğimleri yöntemini kullanacağız.

Her çizginin eğimi bağımsız değişkene eşlik eden sayıdır

$x:$

$m_r = -2$

$m_s = 5$

Bu nedenle iki çizgi arasındaki açı eğim formülü uygulanarak belirlenebilir:

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{-2-5}{1+5\cdot (-2)} \end{vmatrix}=\begin{vmatrix} \cfrac{-7}{-9} \end{vmatrix} = 0,78$

Ve son olarak tanjantı ters çevirerek iki doğru arasındaki açıyı buluyoruz:

$\alpha= \text{tg}^{-1}(0,78) = \bm{37,87º}$

Alıştırma 4

Noktadan geçen doğrunun denklemini bulun

$P(5,-1)$

ve çizgiyle 45° açı yapar

$r.$

Şu satır söylenmelidir:

$\displaystyle r: \ y=2x+4$

Çözüme bakın

Sorunu çözmek için arayacağız

$s$

hesaplayacağımız sağ tarafta. Ayrıca doğrunun eğimini bildiğimiz için eğim yöntemini kullanacağız.

$r:$

$m_r=2$

İki çizgi arasındaki açı formülünden (eğim yöntemi) çizginin eğiminin değerini elde edebiliriz.

$s:$

$\displaystyle \text{tg}(\alpha) =\begin{vmatrix} \cfrac{m_s-m_r}{1+m_r\cdot m_s} \end{vmatrix}$

Bilinen değerleri formülde değiştiririz:

$\displaystyle \text{tg}(45º) =\begin{vmatrix} \cfrac{m_s-2}{1+2\cdot m_s} \end{vmatrix}$

Ve ortaya çıkan denklemi çözmeye çalışıyoruz:

$\displaystyle 1 =\begin{vmatrix} \cfrac{m_s-2}{1+2m_s} \end{vmatrix}$

Denklemin mutlak değeri çözmeyi biraz zorlaştırıyor çünkü hem pozitif hem de negatif seçenekleri analiz etmeniz gerekiyor:

$\displaystyle 1 =+\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=m_s-2$

$\displaystyle 1+2m_s=m_s-2$

$\displaystyle 2m_s-m_s=-2-1$

$\displaystyle m_s=-3$

$\displaystyle 1 =-\cfrac{m_s-2}{1+2m_s}$

$\displaystyle 1 \cdot (1+2m_s)=-(m_s-2)$

$\displaystyle 1+2m_s=-m_s+2$

$\displaystyle 2m_s+m_s=2-1$

$\displaystyle 3m_s=1$

$\displaystyle m_s=\cfrac{1}{3}$

Dolayısıyla iki olası çözümümüz var: eğimi -3 olan bir doğru ve eğimi üçte bir olan başka bir doğru.

Bir doğrunun nokta-eğim denkleminin formülü şöyledir:

$y-y_0=m(x-x_0)$

Dolayısıyla mümkün olan iki doğrunun eğimini bildiğimizde, ifadeye göre her bir doğrunun nokta-eğim denklemini geçmesi gereken noktayla birlikte yazabiliriz,

$P(5,-1):$

$\displaystyle s: \ y+1=-3(x-5) \qquad \qquad s': \ y+1=\cfrac{1}{3}(x-5)$

İki çizgi arasındaki açı (formül)

İki çizgi arasındaki açı nedir?

İki çizgi arasındaki açı nasıl hesaplanır?

Çizgi vektör yönlendirme yöntemi

eğim yöntemi

İki doğru arasındaki açı problemlerini çözme

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Yorum bırakın Yanıtı iptal et