Hiperbolik tanjant fonksiyonu

Bu sayfada hiperbolik tanjant hakkında her şeyi bulacaksınız: formülü nedir, grafik gösterimi, tüm özellikleri…

Hiperbolik tanjant formülü

Hiperbolik tanjant fonksiyonu ana hiperbolik fonksiyonlardan biridir ve tanh(x) sembolüyle temsil edilir. Matematiksel olarak hiperbolik tanjant, hiperbolik sinüsün hiperbolik kosinüse bölünmesine eşittir.

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Hiperbolik sinüs formülünden ve hiperbolik kosinüs formülünden aşağıdaki ifadeye ulaşabiliriz:

$\text{tanh}(x)=\cfrac{e^x-e^{-x}}{e^x+e^{-x}}$

Bu nedenle hiperbolik tanjant fonksiyonu üstel fonksiyonla ilişkilidir. Aşağıdaki bağlantıda bu tür işlevlerin tüm özelliklerini görebilirsiniz:

➤ Bakınız: üstel fonksiyonların özellikleri

Hiperbolik tanjantın grafiksel gösterimi

Formülünden hiperbolik tanjant fonksiyonunu grafiksel olarak temsil edebiliriz:

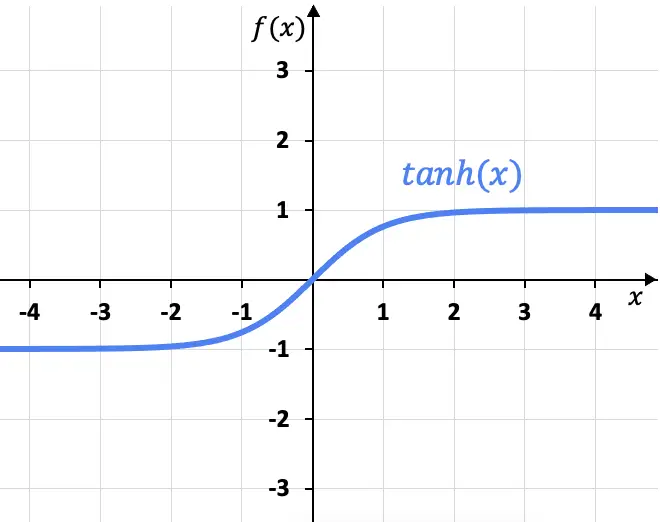
Grafikten görebileceğiniz gibi, hiperbolik tanjant fonksiyonunun x=+1 ve x=-1’de iki yatay asimptotu vardır, çünkü x artı sonsuza yaklaştıkça fonksiyonun limiti x=+1’i verir ve limiti eksi sonsuzdur. x=-1 verir.

Öte yandan hiperbolik tanjant grafiğinin, periyodik bir fonksiyon olan tanjant grafiğiyle (trigonometrik fonksiyon) hiçbir ilgisi yoktur. Aşağıdaki bağlantıda tanjantın grafiksel gösterimini ve hiperbolik tanjanttan nasıl farklı olduğunu görebilirsiniz:

➤ Bakınız: teğet fonksiyonunun grafik gösterimi

Hiperbolik tanjantın özellikleri

Hiperbolik tanjant fonksiyonu aşağıdaki özelliklere sahiptir:

Hiperbolik tanjant fonksiyonunun tanım kümesinin tamamı gerçek sayılardır.

$\text{Dom } f = \mathbb{R}$

Bunun aksine, hiperbolik tanjant fonksiyonunun yolu veya aralığı -1 ile +1 (dahil değil) arasındaki değerlerle sınırlıdır.

$\text{Im } f= (-1,1)$

Hiperbolik tanjant sürekli, bijektif ve tek bir fonksiyondur (koordinatların kökenine göre simetrik).

$\displaystyle \text{tanh}(-x) =- \text{tanh}(x)$

Fonksiyon X eksenini ve Y eksenini koordinat başlangıcında keser.

$(0,0)$

Hiperbolik tanjant fonksiyonunun artı/eksi sonsuzunun sınırları +1/-1’i verir. Dolayısıyla fonksiyonun x=+1’de yatay bir asimptotu ve x=-1’de başka bir yatay asimptotu vardır.

$\displaystyle\lim_{x\to+\infty}\text{tanh}(x)=+1$

$\displaystyle\lim_{x\to-\infty}\text{tanh}(x)=-1$

Hiperbolik tanjant tüm alanı boyunca kesinlikle artmaktadır, bu nedenle göreceli bir ekstrema (ne maksimum ne de minimum) sahip değildir.

Bununla birlikte, x = 0 noktasında fonksiyon dışbükeyden içbükeyliğe değişir, dolayısıyla x = 0, fonksiyonun bir dönüm noktasıdır.

Hiperbolik tanjant fonksiyonunun tersine hiperbolik tanjant (veya hiperbolik arktanjant) argümanı denir ve formülü aşağıdaki gibidir:

$\displaystyle\text{tanh}^{-1}(x)=\text{arg tanh}(x)=\cfrac{1}{2}\ln\left(\frac{1+x}{1-x}\right)$

Hiperbolik tanjant fonksiyonunun türevi 1’in hiperbolik kosinüsün karesine bölümüdür:

$f(x)=\text{tanh}(x) \ \longrightarrow \ f'(x)=\cfrac{1}{\text{cosh}^2(x)}=1-\text{tanh}^2(x)$

Hiperbolik tanjant fonksiyonunun integrali, hiperbolik kosinüsün doğal logaritmasıdır:

$\displaystyle\int\text{tanh}(x) \ dx= \ln\Bigl(\text{cosh}(x)\Bigr)+C$

İki farklı sayının toplamının hiperbolik tanjantı aşağıdaki denklem uygulanarak hesaplanabilir:

$\text{tanh}(x+y)=\cfrac{\text{tanh}(x)+\text{tanh}(y)}{1+\text{tanh}(x)\cdot \text{tanh}(y)}$

Taylor polinomu veya hiperbolik teğet serisi yakınsama yarıçapına sahiptir
$\left|x\right|<\cfrac{\pi}{2}$

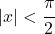
ve aşağıdaki ifadeye karşılık gelir:

$\displaystyle\text{tanh}(x)=x-\frac{x^3}{3}+\frac{2x^5}{15}-\frac{17x^7}{315}+\cdots =\sum_{n=1}^\infty\frac{2^{2n}(2^{2n}-1)B_{2n} x^{2n-1}}{(2n)!}$

Altın

$B_n$

Bernoulli sayısıdır .

Hiperbolik tanjant formülü

Hiperbolik tanjantın grafiksel gösterimi

Hiperbolik tanjantın özellikleri

Yorum bırakın Yanıtı iptal et