Bu makalede bir fonksiyonun hiperbolik arkkozekantının nasıl elde edileceğini açıklıyoruz. Ayrıca hiperbolik arkkozekantın türevinin çalışılmış örneklerini de bulacaksınız.
Hiperbolik kosekant yayın türevinin formülü
X’in ark hiperbolik kosekantının türevi, negatif 1 bölü x çarpı birin kökü artı x karenin çarpımına eşittir.
![]()
Bu nedenle, bir fonksiyonun yay hiperbolik kosekantının türevi, eksi söz konusu fonksiyonun türevinin, fonksiyonun çarpımı çarpı birin kökü artı kare fonksiyonuna bölümüdür.
![]()
Özetle hiperbolik arkkozakant fonksiyonunun türevini hesaplama formülü şöyledir:
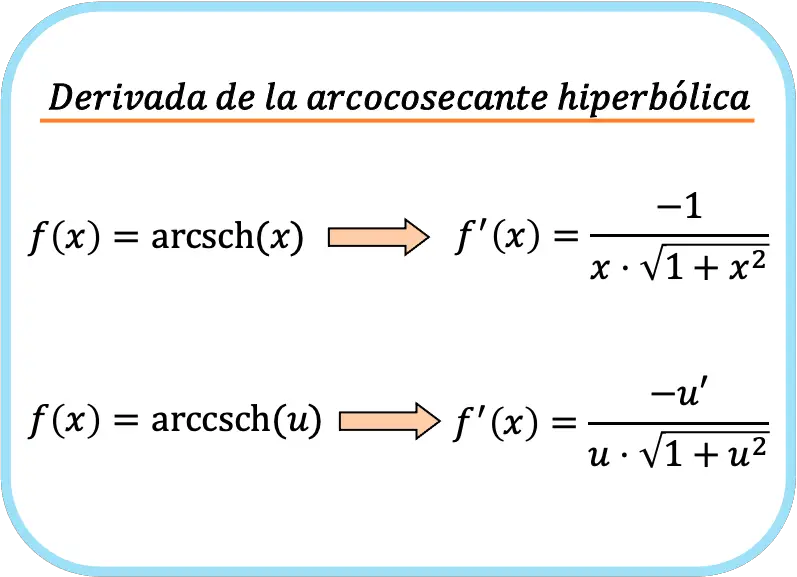
Her ne kadar iki formül koymuş olsak da bu onların farklı olduğu anlamına gelmez. Yakından bakıldığında ikinci formül de birinciye benziyor ancak zincir kuralını uyguluyor.
Hiperbolik kosekant yayının türevine örnekler
Hiperbolik yay kosekantının türevinin formülünü verdikten sonra, bunun gibi iki fonksiyonu türeteceğiz, böylece bunun nasıl yapıldığını görebilirsiniz.
örnek 1
![]()
Bu alıştırmada yay hiperbolik kosekantının türevinin formülünü zincir kuralıyla kullanmalıyız çünkü argümanda x’ten farklı bir fonksiyon vardır:
![]()
Dolayısıyla türevi bulmak için u’yu 3x ile ve u”yu da türevi olan 3 ile değiştirmemiz gerekir:
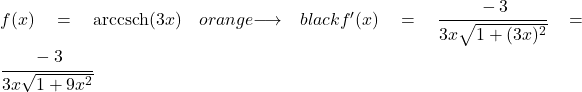
Örnek 2
![]()
Bu durumda hiperbolik yaykozan argümanında bir polinom fonksiyonumuz var, dolayısıyla bunu türetmek için zincir kuralını da kullanmamız gerekiyor:
![]()
Yani kesrin payına argüman fonksiyonunun türevini koyarız ve paydadaki u’yu polinom fonksiyonu ile değiştiririz:
![Rendered by QuickLaTeX.com \begin{aligned}f(x)=\text{arccsch}(x^5-2x^3) \quad\color{orange}\bm{\longrightarrow}\quad\color{black}f'(x)&=\cfrac{-(5x^4-6x^2)}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\\[1.5ex] &=\cfrac{-5x^4+6x^2}{(x^5-2x^3)\sqrt{1+(x^5-2x^3)^2}}\end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-6257584425bd348ba75c7680d8ff6f70_l3.png)