Hiperbolik kosinüs fonksiyonu

Burada hiperbolik kosinüs fonksiyonu hakkında her şeyi bulacaksınız: formülü nedir, grafiksel gösterimi, özellikleri, diğer fonksiyonlarla matematiksel ilişkileri vb.

Hiperbolik kosinüs formülü

Hiperbolik kosinüs fonksiyonu ana hiperbolik fonksiyonlardan biridir ve cosh(x) sembolüyle temsil edilir. Hiperbolik kosinüs, e ^x artı e ^-x’in toplamının 2’ye bölünmesine eşittir.

Bu nedenle hiperbolik kosinüsün formülü şöyledir:

$\displaystyle\text{cosh}(x)=\cfrac{e^{x}+e^{-x}}{2}$

Dolayısıyla hiperbolik kosinüs matematiksel olarak üstel fonksiyonla ilişkilidir. Aşağıdaki bağlantıda bu tür fonksiyonun özelliklerini görebilirsiniz:

➤ Bakınız: üstel fonksiyonun özellikleri

Hiperbolik kosinüsün grafiksel gösterimi

Hiperbolik kosinüs fonksiyonunun grafiksel gösterimi ikinci dereceden bir fonksiyon (veya parabol) biçimindedir:

➤ Bakınız: İkinci dereceden bir fonksiyonun grafiksel gösterimi .

Bu grafikte hiperbolik kosinüsün y eksenine göre simetrik olması nedeniyle çift fonksiyon olduğunu açıkça görebiliyoruz.

Öte yandan hiperbolik kosinüsün grafiği, periyodik bir fonksiyon olan kosinüsün (trigonometrik fonksiyon) grafiğinden çok farklıdır. Kosinüsün grafiksel gösterimini ve hiperbolik kosinüs ile tüm farklarını aşağıdaki bağlantıda görebilirsiniz:

➤ Bakınız: kosinüs fonksiyonunun grafik gösterimi

Hiperbolik kosinüsün özellikleri

Hiperbolik kosinüs aşağıdaki özelliklere uyar:

Hiperbolik kosinüs fonksiyonunun alanının tamamı gerçek sayılardır:

$\text{Dom } f = \mathbb{R}$

Bunun yerine, hiperbolik kosinüs fonksiyonunun aralığı (veya aralığı) 1’dir ve 1’den büyük tüm sayılar:

$\text{Im } f= [1,+\infty)$

Hiperbolik kosinüs sürekli ve eşit bir fonksiyondur.

$\displaystyle \text{cosh}(-x)=\text{cosh}(x)$

Fonksiyon Y eksenini x=0 noktasında kesiyor.

$(0,1)$

Öte yandan fonksiyonun X ekseni ile kesişme noktası yoktur.

Hiperbolik kosinüs fonksiyonunun sonsuza giden iki limiti (pozitif ve negatif) artı sonsuzluğu verir.

$\displaystyle\lim_{x\to+\infty}\text{cosh}(x)=+\infty$

$\displaystyle\lim_{x\to-\infty}\text{cosh}(x)=+\infty$

Hiperbolik kosinüs x = 0’a kadar azalır ve bu noktadan sonra süresiz olarak artar, dolayısıyla fonksiyonun minimumu x = 0’dadır.

$(0,1)$

Fonksiyon tanım kümesi boyunca dışbükey olduğundan herhangi bir dönüm noktası yoktur.

Hiperbolik kosinüs fonksiyonunun türevi hiperbolik sinüstür:

$f(x)=\text{cosh}(x) \ \longrightarrow \ f'(x)=\text{senh}(x)$

Hiperbolik kosinüs fonksiyonunun integrali hiperbolik sinüstür:

$\displaystyle \int \text{cosh}(x) \ dx= \text{senh}(x) + C$

Hiperbolik kosinüs fonksiyonunun Taylor polinomu (veya Maclaurin serisi) aşağıdaki gibidir:

$\displaystyle\text{cosh}(x)=1+\cfrac{x^2}{2!}+\cfrac{x^4}{4!}+\cfrac{x^6}{6!}+\dots=\sum_{n=0}^\infty\cfrac{x^{2n}}{(2n)!}$

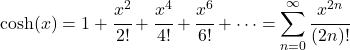
Hiperbolik kosinüs fonksiyonunun Laplace dönüşümü aşağıdaki gibidir:

$\mathcal{L}\bigl[\text{cosh}(at)\bigr]=\cfrac{s}{s^2-a^2}$

Hiperbolik kosinüsün matematiksel ilişkileri

Daha sonra, hepsi matematiksel olarak birbiriyle ilişkili olduğundan hiperbolik kosinüsün diğer hiperbolik fonksiyonlardan nasıl hesaplanabileceğini göreceğiz.

Temel denklem hiperbolik kosinüsü hiperbolik sinüsle ilişkilendirir:

$\text{cosh}^2(x)-\text{senh}^2(x)=1$

➤ Bakınız: hiperbolik sinüs

Üç ana hiperbolik fonksiyon (hiperbolik sinüs, kosinüs ve tanjant) aşağıdaki denklemle ilişkilendirilebilir:

$\text{tanh}(x)=\cfrac{\text{senh}(x)}{\text{cosh}(x)}$

Öte yandan, iki farklı sayının toplanmasının (veya çıkarılmasının) hiperbolik kosinüsü aşağıdaki formüllerle belirlenebilir:

$\text{cosh}(x+y)=\text{cosh}(x)\text{cosh}(y)+\text{senh}(y)\text{senh}(x)$

$\text{cosh}(x-y)=\text{cosh}(x)\text{cosh}(y)-\text{senh}(y)\text{senh}(x)$

Bir sayının iki katının hiperbolik kosinüsü, hiperbolik kosinüsün kareleri ile bu sayının hiperbolik sinüsünün toplamına eşittir:

$\text{cosh}(2x)=\text{cosh}^2(x)+\text{senh}^2(x)$

İki hiperbolik kosinüsün toplanması veya çıkarılması aşağıdaki formüller uygulanarak hesaplanabilir:

$\displaystyle\text{cosh}(x)+\text{cosh}(y)=2\text{cosh}\left(\frac{x+y}{2}\right)\text{cosh}\left(\frac{x-y}{2}\right)$

$\displaystyle\text{cosh}(x)-\text{cosh}(y)=2\text{senh}\left(\frac{x+y}{2}\right)\text{senh}\left(\frac{x-y}{2}\right)$

Son olarak hiperbolik kosinüsün karesi aşağıdaki formülle hesaplanabilir:

$\text{cosh}^2(x)=\cfrac{1}{2}\Bigl(\text{cosh}(2x)+1\Bigr)$

Hiperbolik kosinüs formülü

Hiperbolik kosinüsün grafiksel gösterimi

Hiperbolik kosinüsün özellikleri

Hiperbolik kosinüsün matematiksel ilişkileri

Yorum bırakın Yanıtı iptal et