Hiperbolik arkkotanjantın türevi

Bu makalede bir fonksiyonun hiperbolik arkkotanjantının nasıl elde edileceğini açıklıyoruz. Ek olarak hiperbolik arkkotanjantın türevinin çözülmüş örneklerini görebileceksiniz.

Hiperbolik arkkotanjantın türevinin formülü

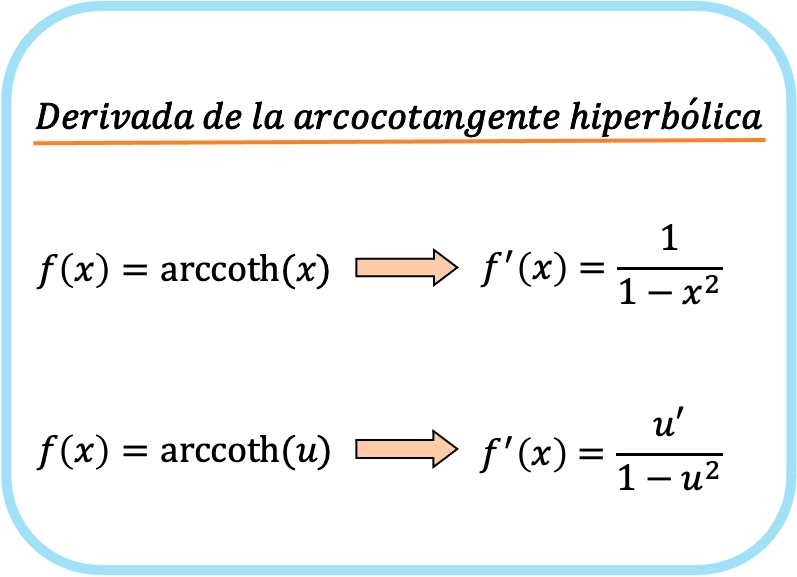
X’in hiperbolik arkkotanjantının türevi bir bölü bir eksi x’in karesidir.

f(x)=\text{arccoth}(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{1}{1-x^2}

Bu nedenle, bir fonksiyonun hiperbolik arkkotanjantının türevi, o fonksiyonun türevinin bir eksi o fonksiyonun karesine bölünmesine eşittir.

f(x)=\text{arccoth}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

İkinci formülün birinciye benzediğini ancak zincir kuralını uyguladığını, yani aslında aynı formül olarak kabul edilebileceklerini unutmayın.

hiperbolik arkkotanjanttan türetilmiştir

Bazı matematik kitaplarında bu tip ters trigonometrik fonksiyonun türevinin şöyle olduğunu görebilirsiniz:

f'(x)=\cfrac{-1}{x^2-1}

Ancak yakından bakıldığında aynı formüller olduklarını, tek fark kesrin pay ve paydasının -1 ile çarpılmış olmasıdır.

Hiperbolik arkkotanjantın türevi örnekleri

örnek 1

f(x)=\text{arccoth}(5x)

Hiperbolik arkkotanjant argümanında x’ten farklı bir fonksiyona sahibiz, dolayısıyla bunu türetmek için zincir kuralı formülünü kullanmamız gerekir:

f(x)=\text{arccoth}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

5x’in türevi 5’tir, dolayısıyla kesrin payına 5, paydasına da eksi 5x kare koyun:

f(x)=\text{arccoth}(5x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{5}{1-(5x)^2}}=\cfrac{5}{1- 25x^2}

Örnek 2

f(x)=\text{arccoth}(e^{3x})

Bu fonksiyonun türevini çözmek için hiperbolik arkkotanjantın türevine yönelik aşağıdaki formülü uygulamamız gerekir:

f(x)=\text{arccoth}(u) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{u'}{1-u^2}

Bu durumda, trigonometrik fonksiyonun argümanında üstel bir fonksiyon olduğundan bileşik bir fonksiyonumuz var. Dolayısıyla tüm fonksiyonun türevini bulmak için zincir kuralını kullanmamız gerekiyor:

f(x)=\text{arccoth}(e^{3x}) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} f'(x)=\cfrac{3\cdot e^{3x}}{1-\left(e^{3x}\right)^2}=\cfrac{3e^{3x}}{1-3^{6x}}

Benzer ürünler

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top