Burada hiperbol hakkında her şeyi bulacaksınız: nedir, karakteristik unsurları nelerdir, denklemi nasıl bulunur, örnekler, çözülmüş alıştırmalar vb.
Abartılılık nedir?
Hiperbol, matematiksel tanımı aşağıdaki gibi olan iki dallı açık bir eğridir:
Analitik geometride bir hiperbol, düzlem üzerinde aşağıdaki koşulu karşılayan noktaların odağıdır: Hiperbolün herhangi bir noktası ile iki sabit nokta (odak adı verilen) arasındaki mesafe farkının mutlak değeri sabit olmalıdır.
Ayrıca bu iki mesafenin çıkarılması değeri her zaman hiperbolün iki köşesi arasındaki mesafeye eşdeğerdir.
![]()

Aşağıda katsayının ne anlama geldiğini göreceğiz.
![]()
bir abartı.
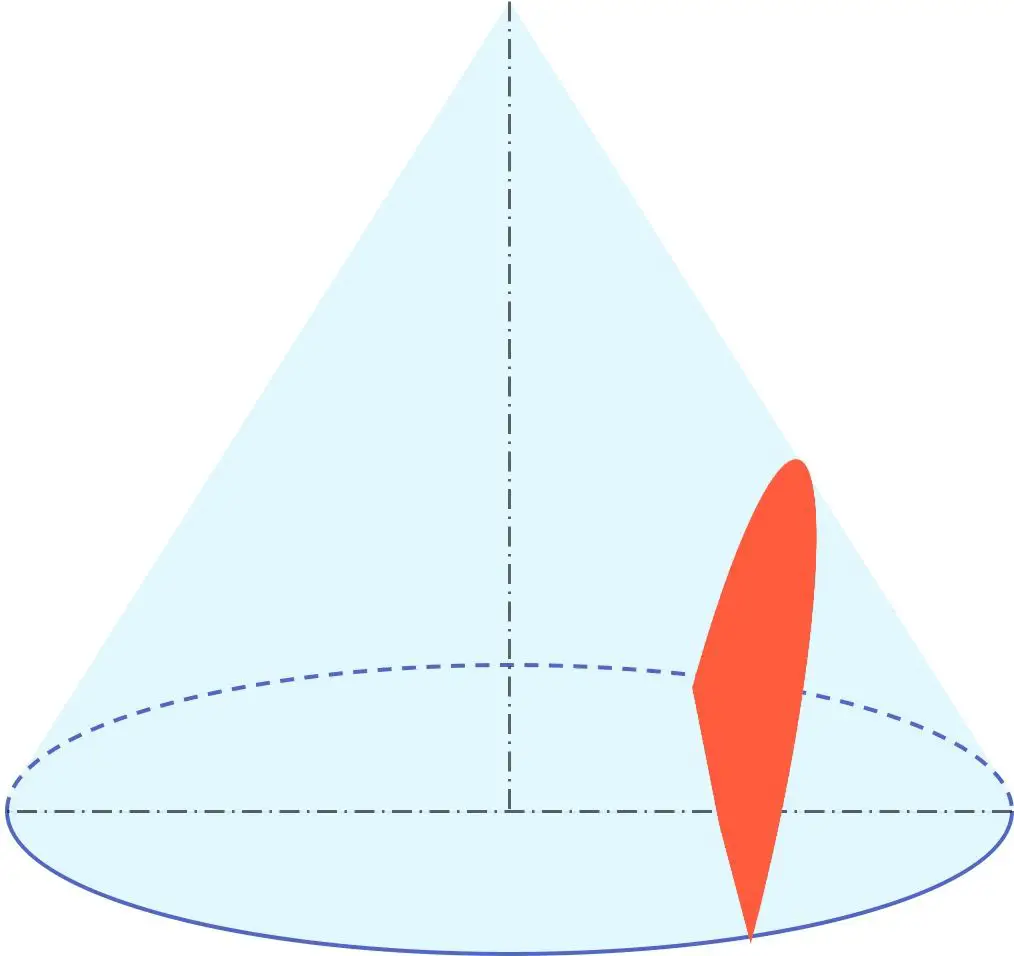
Ayrıca hiperbol, çevre, elips ve parabol ile birlikte konik adı verilen geometrik grubun bir parçasıdır. Dolayısıyla hiperbol bir konik kesittir, yani bir koniden elde edilebilir.
Özellikle bir hiperbol, bir koninin, dönme eksenine göre koni üretecinin oluşturduğu açıdan daha küçük bir açıya sahip bir düzlem tarafından kesilmesinin sonucudur.
Bir hiperbolün elemanları
Bir hiperbolün özellikleri aşağıdakilere bağlıdır:
- Odaklar : bunlar her hiperbolün karakteristiği olan iki sabit noktadır (aşağıdaki grafikte F ve F’ noktaları). Hiperbolün herhangi bir noktasından her odağa olan mesafeler arasındaki farkın mutlak değeri sabit ve eşittir

- Odak veya ana eksen : Hiperbolün iki odağından geçen çizgidir. Söz konusu geometrik şeklin simetri eksenine karşılık gelir. Enine veya enine eksen olarak da adlandırılır.
- İkincil eksen : FF’ doğru parçasının (B ve B’ noktalarından geçen çizgi) ortaydır. Ayrıca odak eksenine dik bir çizgidir ve hiperbolün diğer bir simetri eksenidir.
- Merkez (O) : iki eksenin kesişme noktası ve iki köşe ile iki odağın orta noktasıdır. Hiperbolün iki simetri ekseni olduğundan aynı zamanda simetri merkezidir.
- Köşeler (A ve A’) : hiperbolün dallarının odak ekseni ile kesişme noktalarıdır.
- Vektör ışınları (R) : bunlar hiperbol üzerindeki herhangi bir noktadan her odağa giden bölümlerdir.
- Odak uzaklığı : Bu, iki odak arasındaki kompozit segmentin uzunluğudur.
- Ana eksen veya gerçek eksen: A noktasından A’ noktasına giden parçadır, uzunluğu şuna eşittir:

- Küçük eksen veya hayali eksen: B noktasından B’ noktasına giden doğru parçasıdır, uzunluğu şuna eşittir:
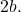
- Asimptotlar : grafikte gösterilen noktalı çizgilerdir. Aşağıda bunların nasıl hesaplandığını göreceğiz.
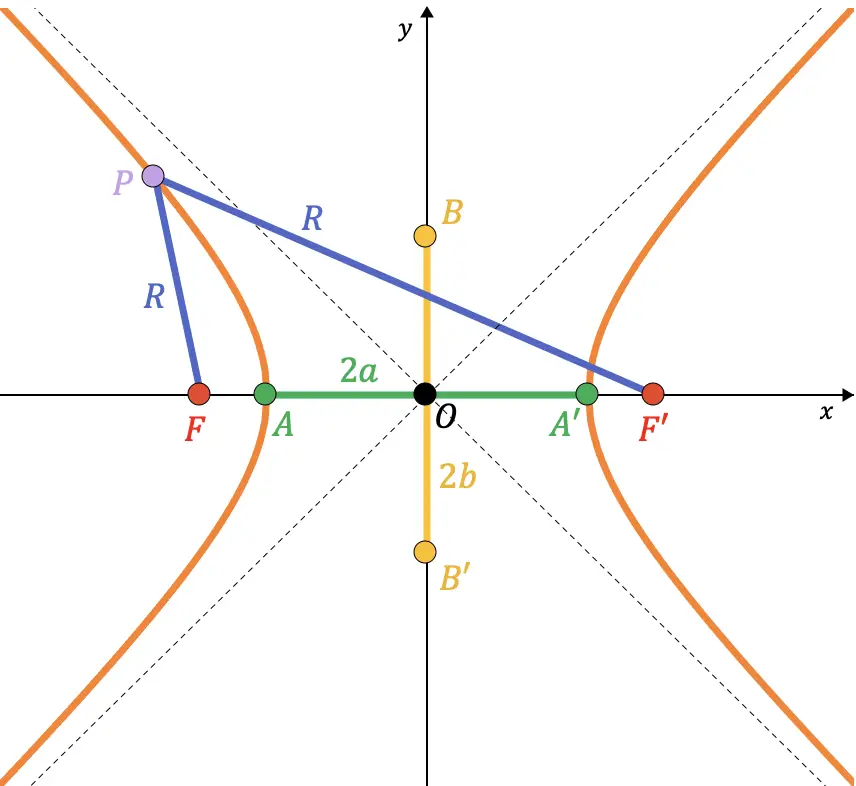
Bir hiperbolün elemanları arasındaki ilişki
Öncelikle yarım eksenin bir eksenin yarısı anlamına geldiğini söylüyoruz. Örneğin, gerçek yarı eksen, A noktasından hiperbolün merkezine giden ve uzunluğu
![]()
Dolayısıyla gerçek yarım eksen, hayali yarım eksen ve yarım odak uzaklığı arasında çok önemli bir ilişki vardır. Aslında bundan sonra çıkaracağımız formül hiperbol egzersizleri ve problemlerinin çözümünde çokça kullanılıyor.
Bir hiperbolün B ve B’ noktalarının, asal eksen ile sanal yarıçap çemberinin kesişme noktalarına karşılık geldiğini bilmelisiniz.
![]()
(yarı odak uzaklığı) merkezden A noktasına. Dolayısıyla aşağıdaki grafik gösterimde de görebileceğiniz gibi, A noktası ile B noktasını birleştiren doğru parçası, söz konusu dairenin yarıçapı () ile çakışmaktadır.
![]()
):
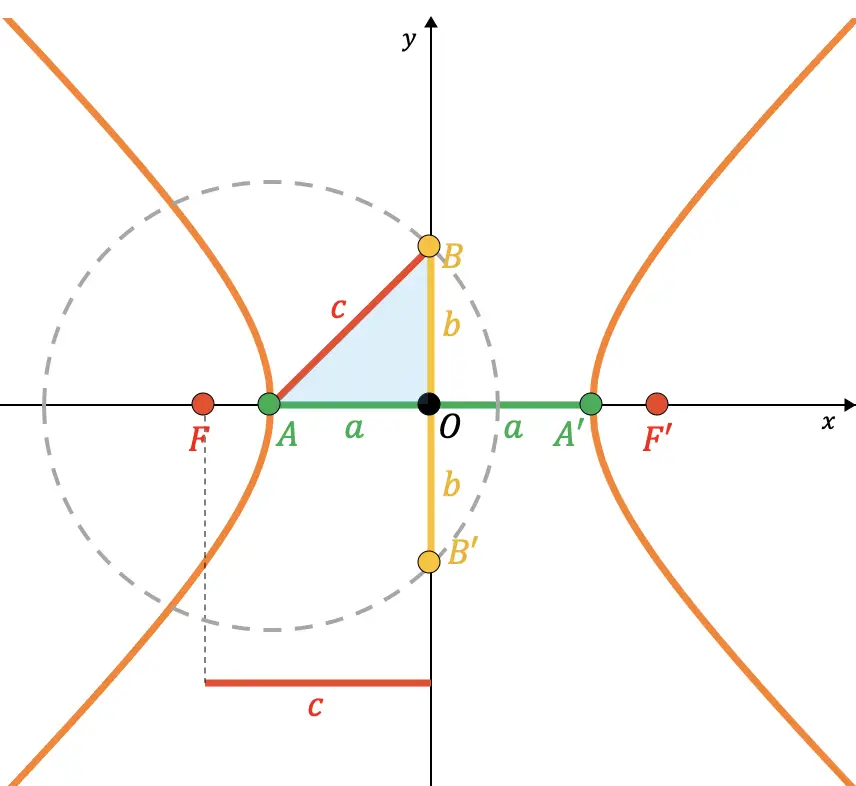
Dolayısıyla Pisagor teoreminden parametreler arasındaki ilişkinin gösterilebilir.
![]()
Ve
![]()
takip ediliyor:
![]()
hiperbol denklemi
Hiperbol denklemlerinin birkaç türü vardır, çünkü özelliklerine bağlı olarak biri veya diğeri onu matematiksel olarak ifade etmek için kullanılır. Daha sonra her birini ayrıntılı olarak analiz edeceğiz.
İlk olarak hiperbolün sıradan denklemine sahibiz. İkinci olarak, sıradan denklemin bir varyantını göreceğiz; bu, hiperbolün indirgenmiş veya kanonik denklemidir . Daha sonra bir hiperbolün genel denkleminin nasıl olduğunu inceleyeceğiz. Ve son olarak, iki özel hiperbol durumunun denklemlerini analiz edeceğiz: eşkenar hiperbol ve eşlenik hiperboller .
Hiperbolün sıradan denklemi
Koordinatların orijininde ((0,0) noktası) bir dış merkezi olan bir hiperbolü bir denklemle tanımlamak istediğimizde, aşağıdaki formülü kullanmalıyız:
Kartezyen koordinatlarda hiperbolün sıradan denkleminin formülü aşağıdaki gibidir:
![]()
Altın:
-

Ve

hiperbolün merkezinin koordinatları:
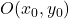
-

hiperbolün yarı ana ekseninin uzunluğudur.
-

hiperbolün yarı küçük ekseninin uzunluğudur.
Bu denklemle, odak ekseni yatay olan (dalları sağa ve sola açık olan) hiperbolleri tanımlayabilirsiniz; normalde hiperboller böyledir. Ancak dikey bir odak ekseniyle çalışırsak (dallar yukarıdan aşağıya doğru açıksa), negatif işaret y değişkeninden x değişkenine geçer:
![]()
Altın
![]()
Ve
![]()
daha önce olduğu gibi hiperbolün merkezinin koordinatları ve terimlerdir
![]()
Ve
![]()
bunlar hala hiperbolün yarı ana ekseni ve yarı küçük eksenidir, ancak öncekinden farklı olarak bu ikisi artık sırasıyla dikey ve yatay olarak yönlendirilecektir.
Hiperbolün kanonik veya indirgenmiş denklemi
Bu tür hiperbol denklemi sıradan denklemlere çok benzer, tek fark kanonik denklemin merkezi (0,0) noktası olan hiperbolleri analitik olarak ifade etmek için kullanılmasıdır. Bu nedenle, hiperbolün merkezi koordinatların orijini olduğunda hiperbolün kanonik veya indirgenmiş denklemini kullanırız.
Şimdi hiperbolün indirgenmiş denkleminin formülünü normal denkleminden çıkaracağız:
![]()
Eğer hiperbolün merkezi koordinatların orijini, yani (0,0) noktası olacaksa, aşağıdaki ifade her zaman doğru olacaktır:
![]()
![]()
Böylece hiperbolün kanonik veya indirgenmiş denklem formülü şöyle olacaktır:
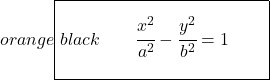
Daha önce olduğu gibi, odak ekseni yatay yerine dikey olsaydı negatif değişken x olurdu:
![]()
Hiperbolün genel denklemi
Bir hiperbolün genel denkleminin formülü aşağıdaki gibidir:
![]()
Ancak yukarıdaki denklemin hiperbol olması için katsayılar
![]()
Ve
![]()
Sıfırdan farklı olmalı ve aynı zamanda zıt işarete sahip olmalıdırlar.
Eşkenar hiperbol denklemi
Eşkenar hiperbol, gerçek yarı eksenin uzunluğunun hayali yarı eksenin uzunluğuna eşit olduğu bir hiperboldür; bu şu anlama gelir:
![]()
Bu nedenle eşkenar hiperbolün denklemi şöyledir:
![]()
Ayrıca eşkenar hiperbollerin asimptotları birbirine diktir. Ve bu doğruların denklemleri aşağıdaki gibidir:
![]()
![]()
Dikkatli bakarsak, bu iki denklem sırasıyla birinci (ve üçüncü) çeyreğin ve ikinci (ve dördüncü) çeyreğin açıortaylarıdır. Yani bir eşkenar hiperbolü 45° sola döndürürsek asimptotları koordinat eksenlerinin yerini alır:
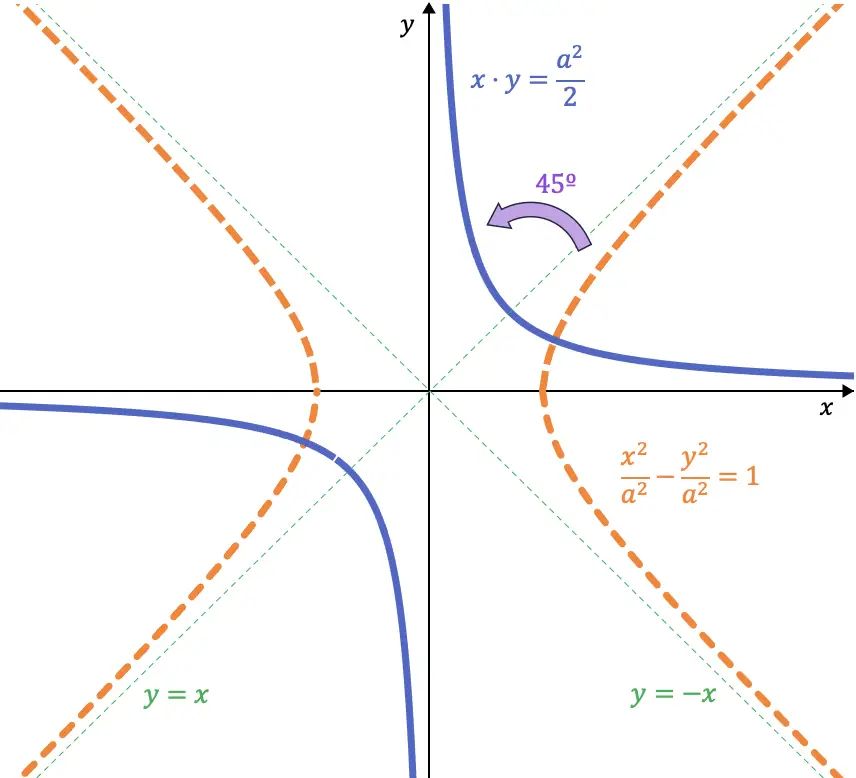
Yani 45° dönüş yaptığımızda hiperbolün denklemi şöyle olur:
![]()
konjuge hiperboller
Birinin gerçek ekseni diğerinin hayali eksenine eşitse iki hiperbol eşleniktir . Bu nedenle iki eşlenik hiperbolün denklemleri arasındaki tek fark hangi değişkenin olumsuzlandığıdır çünkü paydaların katsayıları aynı kalmalıdır.
Birbirine konjuge iki hiperbolün denklemlerine bir örnek:
![]()
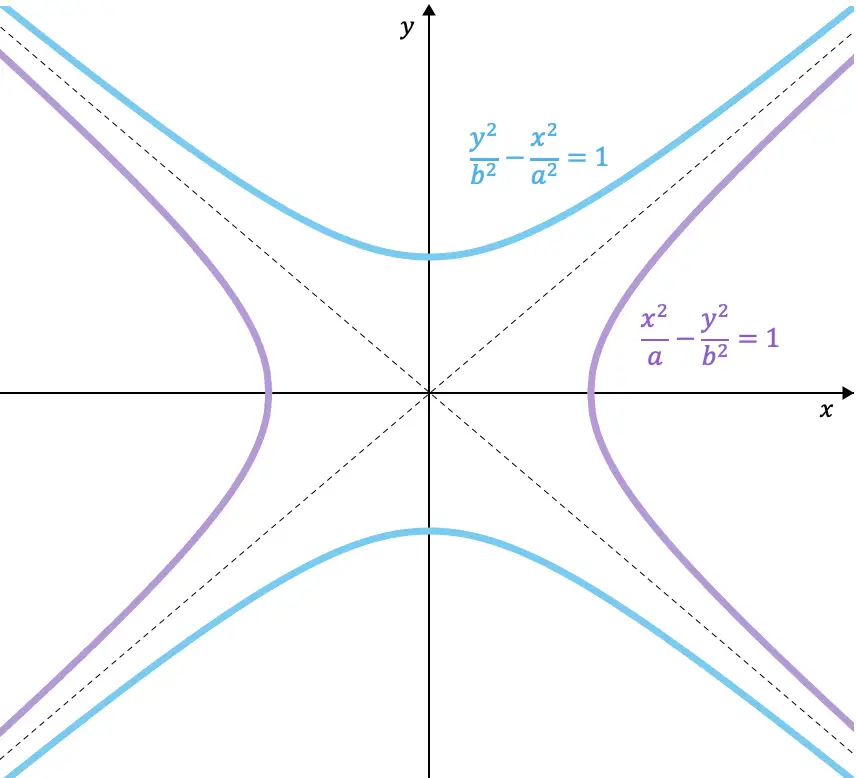
Ek olarak, grafiği çizilen hiperbollerden de görebileceğiniz gibi, eşlenik hiperboller aynı asimptotları paylaşmaktadır.
Hiperbolün asimptotları
Önceki grafiklerde gördüğünüz gibi her hiperbolün iki asimptotu vardır. Asimptotun, bir fonksiyona çok yaklaşan ancak onunla hiçbir zaman tam olarak kesişmeyen veya ona dokunmayan düz bir çizgi olduğunu unutmayın.
Dolayısıyla hiperbollerin asimptotlarına karşılık gelen formüller şunlardır:
![]()
![]()
Böylece herhangi bir hiperbolün asimptotları katsayıları kullanılarak kolaylıkla belirlenebilir.
![]()
Ve
![]()
bunlar sırasıyla hiperbolün gerçek yarı ekseninin ve sanal yarım ekseninin uzunluklarıdır.
Hiperbolün dışmerkezliği
Bir hiperbolün dışmerkezliği, onun ne kadar açık veya kapalı olduğunu belirleyen karakteristik bir parametredir. Sayısal olarak, bir hiperbolün dışmerkezliği, yarı odak uzunluğunun gerçek yarı eksenine bölünmesiyle hesaplanır:
![]()
Herhangi bir hiperbolün dışmerkezliği her zaman 1’den büyüktür:
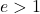
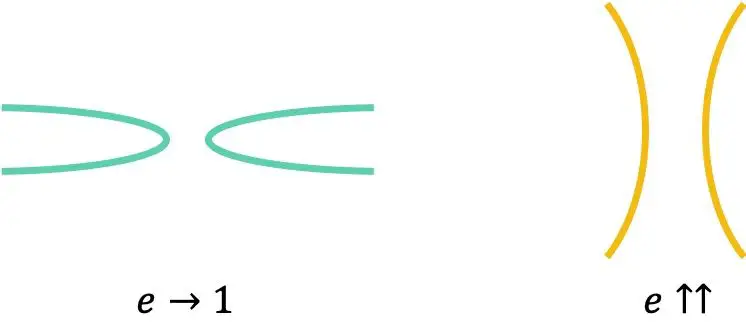
Son olarak, bir eşkenar hiperbolün dışmerkezliğinin her zaman şuna eşit olduğuna dikkat edilmelidir:
![]()
Hiperbol problemleri çözüldü
Aşağıda hiperbol ve hiperbol denklemiyle ilgili problemlerde ve çözülmüş alıştırmalarda gördüğümüz kavramları uygulayabilirsiniz.
1. Egzersiz
Merkezi (-1.3) noktasında olan, gerçel yarı eksen uzunluğu 3 birim ve sanal yarı eksen uzunluğu (Y eksenine paralel) 7 birim olan hiperbolün denklemi nedir?
Hiperbolün denklemini bulmak için hiperbolün normal denkleminin formülünü uygulamanız yeterlidir:
![]()
Hiperbolün merkezinin koordinatlarını denklemde yerine koyarız:
![]()
![]()
Ve son olarak bilinmeyenlerin değerlerini yerine koyuyoruz
![]()
Ve
![]()
![]()
![]()
Alıştırma 2
Denklemi şu şekilde tanımlanan hiperbolün merkezinin koordinatlarını, köşelerini, odaklarını, dışmerkezlik değerini ve asimptotlarını bulun:
![]()
Öncelikle şunu belirtelim ki denklemdeki negatif değişken y değişkeni olduğundan hiperbolün dalları sağa ve sola (odak ekseni X eksenine paralel) açılacaktır.
İkincisi, denklem hiperbolün kanonik (veya indirgenmiş) denklemine karşılık gelir, dolayısıyla merkezi koordinatların orijini olur.
![]()
Hiperbolün merkezini bildiğimizde, diğer her şeyi hesaplamak için gerçek yarı eksenin (parametre) değerini bulmamız gerekir.
![]()
) ve hayali yarım eksen (parametre
![]()
). Her ikisini de hiperbolün kanonik (veya indirgenmiş) denkleminin formülünden çıkarabiliriz:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Yani merkez ile köşeler arasında 5 birimlik bir mesafe varsa, bu hiperbollerin köşelerinin şöyle olduğu anlamına gelir:
![]()
Her odak noktasının koordinatlarını belirlemek için yarım odak uzaklığının değerini bilmeniz gerekir (parametre
![]()
). Bunun için hiperbolün elemanlarını birleştiren formülü kullanabiliriz:
![]()
![]()
![]()
Dolayısıyla merkez ile evler arasında 13 birimlik bir alan bulunuyor. Buna göre her hanenin koordinatları şöyledir:
![]()
Daha sonra hiperbolün dışmerkezliğini hesaplamak için ilgili formülü kullanmamız gerekir:
![]()
Ve son olarak hiperbolün asimptotlarını formülleriyle buluyoruz:
![]()
![]()
Alıştırma 3
Hiperbolün bir noktasından F(-4.0) ve F(4.0) odaklarına olan mesafeler arasındaki farkın 6 birim olduğunu bilerek, koordinatların orijini merkezli hiperbolün denklemini hesaplayın.
İlk olarak, hiperbolün merkezi koordinatların orijininde olduğundan kanonik veya indirgenmiş denklemi kullanacağız:
![]()
O halde, bir hiperbolün tanımına göre, noktalarından birinden odaklara olan mesafelerin farkının mutlak değeri (bu durumda 6’dır) gerçek eksenin uzunluğuna eşit olmalıdır (
![]()
). Henüz:
![]()
![]()
![]()
![]()
Öte yandan hiperbolün merkezi (0,0) noktasıdır ve odak noktası da (4,0) noktasıdır. Böylece iki noktaya olan mesafe (parametre
![]()
) 4 birimdir.
![]()
Artık parametrenin değerini biliyoruz
![]()
hiperbolün 3 karakteristik katsayısı arasındaki matematiksel ilişki ile:
![]()
![]()
![]()
![]()
Yani hiperbolün denklemi şöyledir:
![]()
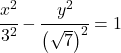
![]()