Sanal sayılar kümesini veya sanal birimi mutlaka duymuşsunuzdur. Gerçel sayılara ait olmayan sayıların matematiksel olarak ifade edilmesi ihtiyacından doğan matematiksel bir kavramdır.
Sanal sayılar nedir?
Sanal sayılar, kareleri alındığında negatif bir sayı veren sayılardır. Dolayısıyla bunlar negatif bir sayının kareköküne eşdeğer değerlerdir. Örneğin sanal birim (i sayısı) -1’in kareköküne eşittir.
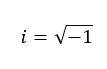
Bu sayılar reel sayılara ait değildir çünkü reel sette negatif kökler çözümlenemez. Hayali ortamın önemi de burada yatıyor. Bu set, negatif köklerle başa çıkabilmek ve bize negatif bir kök verdikleri için “çözümü olmayan” tüm denklemleri ve ikinci dereceden problemleri çözebilmek için icat edildi.
Karışıklığı önlemek için sanal sayılar ile karmaşık sayılar arasında ayrım yapmak önemlidir. Kompleksler bir reel sayı ve bir sanal sayıdan oluşan sayılardır. Dolayısıyla hayaller, gerçek kısmı olmayan komplekslerin bir alt kategorisidir. Aşağıdaki tabloda farklılıkları daha iyi anlayacaksınız.
| karmaşık sayı | kraliyet partisi | hayal gücü kısmı | Tanım |
| 4+7i | 4 | 7i | Karmaşık |
| 3 | 3 | 0 | saf kraliyet |
| 2i | 0 | 2i | Saf hayalgücü |
Bu dijital seti yerleştirmeyi tamamlamak için aşağıdaki resimde tüm setlerin yapısını görselleştirebiliriz. Gördüğümüz gibi karmaşık sayılar tüm sayı türlerini kapsar ve bunlar sırasıyla gerçek sayılara ve saf sanal sayılara (bu makalede ele alacağımız sayılar) bölünebilir.

Sanal Sayılara Örnekler
Sanal birim (i)’den diğer sanal sayıları çıkarabiliriz. Aşağıdaki formülü uygulamanız yeterlidir:
m = ri
m sanal bir sayı, r gerçek sayı ve i sanal birimdir. Aşağıdaki resimde negatif köklerden nasıl farklı imajinasyonlar elde ettiğimizi görebilirsiniz.
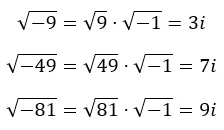
Aslında bunu aşağıdaki ifadeye çıkarabiliriz:
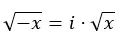
Sanal sayıların özellikleri
Sanal sayıların çok sayıda ilginç özelliği vardır. Bazıları hakkında bu makalenin başında zaten konuştuk, diğerleri ise:
- Hayali varlıklar gerçeklikler kümesine ait değildir çünkü onlar fiziksel olarak var olmayan ve gerçekliğimizde temsil edilemeyen sayılardır.
- Bunlar negatif köklere eşdeğer değerlerdir.
- Hayali çizgi üzerinde grafiksel olarak temsil edilebilirler.
- Hayali güçler (bu, bir sonraki bölümde açıklayacağımız bir kavramdır), sanal değerler içeren sayısal hesaplamaların basitleştirilmesinde çok yardımcıdır.
- Euler formülü, sanal sayıları gerçek sayılarla ilişkilendirmenizi sağlayan bir ifadedir.
Sanal sayılarla işlemler
Artık sanal sayıların tüm önemli özelliklerini bildiğinize göre, onlarla işlemleri nasıl çözeceğinizi öğrenmenin zamanı geldi. Hayali değerlerle çalışmak için, gerçek değerlerle çalışmak için izlediğiniz adımların aynısını izlemelisiniz; tek fark, tek bir kavramı hesaba katmanızdır: hayali güçler.
hayal gücü
Sanal sayıların, sanal birimi kendisiyle çarptığınızda ortaya çıkan çok ilginç bir özelliği vardır. Yani hayali birliğin güçlerini yaptığınızda bu olur. Aşağıdaki listedeki gibi kuvvetleri yazarsak bir model keşfedilebilir:
ben 0 = 1
ben 1 = ben
ben 2 = ben · ben = ( √ -1) · ( √ -1) = -1
ben 3 = ben 2 ben = (-1) ben = -i
ben 4 = ben 2 ben 2 = (-1) (-1) = 1
Bu kavramı bilmek sanal sayılarla işlemleri çözmemizi çok kolaylaştıracaktır çünkü zor işlemleri basitleştirip biraz daha kolaylaştırabileceğiz. Ayrıca bu güçlerin iyi yanı, süresiz olarak tekrarlanmalarıdır. Birkaç güç daha eklersek bunu görebiliriz:
ben 5 = ben
ben 6 = -1
ben 7 = -i
ben 8 = 1
vesaire.
Ve negatif güçlerde de bu olur.
Sanal sayılarla aritmetik işlemler
Daha sonra size her temel aritmetik işlemin bir örneğini vereceğiz, böylece hayali sayı hesaplamalarının çözüldüğünü görebilirsiniz.
- Sanal sayıların eklenmesi: Gerçek sayıların toplanmasıyla tamamen aynıdır, yalnızca i’yi eklemeyi unutmayın.
4i + 3i = 7i
- Sanal sayılarda çıkarma: Çıkarma işlemleri de gerçek kümede olduğu gibi çözülür.
4i – 3i = ben
- Sanal sayıların çarpımı: Bu durumda daha önce bahsettiğimiz sanal kuvvetleri aklımızda tutmalıyız.
3i 4i = 12 ben 2 = 12 (-1) = -12
- Sanal sayıların bölünmesi: Bu tür bölme işleminde, işlemi basitleştirmemize olanak tanıyan hayali bir güçle karşılaşmamız durumunda da dikkatli olmalıyız.
12i ÷ 4i = 3
Sanal sayılarla denklemler
Daha önce de söylediğimiz gibi denklemleri gerçel sette çözdüğümüzde bazen negatif kökler elde ederiz ve dolayısıyla denklemlerin “çözümleri yoktur” . Ancak artık imajinerleri bildiğimize göre bu denklemleri çözebiliriz. Bir örnek görelim:
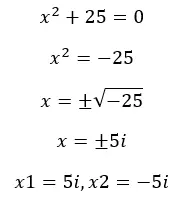
Sanal sayılar ne için kullanılır?
Sanal sayılar, gerçek kümenin dışındaki değerleri ifade edebilme ihtiyacından kaynaklanmaktadır. Bu nedenle ilk bakışta çok fazla kullanışlı uygulamaları yokmuş gibi görünebilir. Ancak gerçek şu ki durum tam tersi. Çünkü bunları reel sayılarla birleştirdiğimizde karmaşık sayıları elde ederiz.
Ve bunların birçok uygulaması var. Alternatif akımı incelemek için kullanılırlar (çünkü negatif değerlere sahiptir), ayrıca dalga alanında (fizik, telekomünikasyon elektroniği ve kuantum mekaniği uygulamaları vardır) kullanımı da oldukça yaygındır. Diğer birçok kullanım arasında.
Buna ek olarak, ikinci dereceden bir denklemi çözdüğünüzde, değerin size negatif bir kök verdiği ve işlem yapamayacağınız sıklıkla görülür… Hayali araçlarla bunları çözebilirsiniz . Yani sonuç olarak daha soyut bilgimizi genişletmemizi sağlayan bir set diyebiliriz.