Bu yazıda bir fonksiyonun periyodikliğinin ne olduğunu açıklıyoruz. Ayrıca periyodik fonksiyonların çeşitli örneklerini göreceksiniz. Son olarak trigonometrik fonksiyonların en önemli özelliklerinden biri olduğu için periyodunu analiz edeceğiz.
Bir fonksiyonun periyodikliği nedir?
Bir fonksiyonun periyodikliği, değerlerini döngüsel olarak tekrarlayan fonksiyonların bir özelliğidir, yani bir fonksiyon, grafiği belirli aralıklarla tekrarlanıyorsa periyodiktir. Bu aralığa periyot denir.
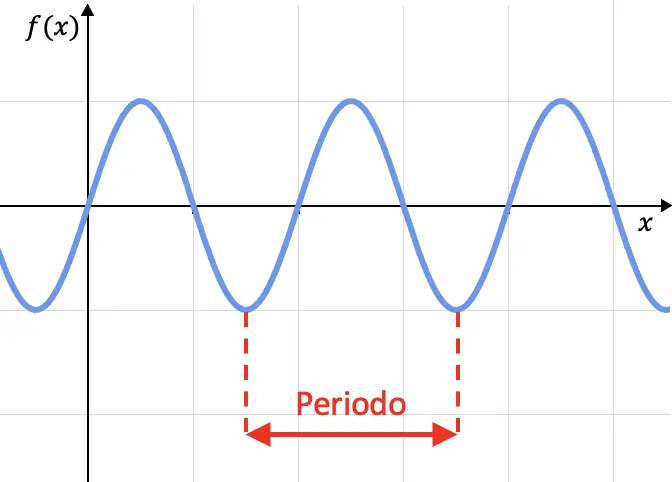
Matematiksel olarak bir fonksiyon sadece yerine getiriliyorsa periyodik olarak tanımlanır.
![]()
bağımsız değişken x’in herhangi bir değeri için.
![]()
T, i k tamsayı periyodik fonksiyonunun periyodudur.
Fonksiyon periyodikliklerine örnekler
Bir fonksiyonun periyodikliği kavramını gördükten sonra, bir fonksiyonun periyodikliğinin nasıl hesaplanacağına dair birkaç örnek göreceğiz.
örnek 1
Aşağıdaki fonksiyonun periyodik olup olmadığını belirleyin:
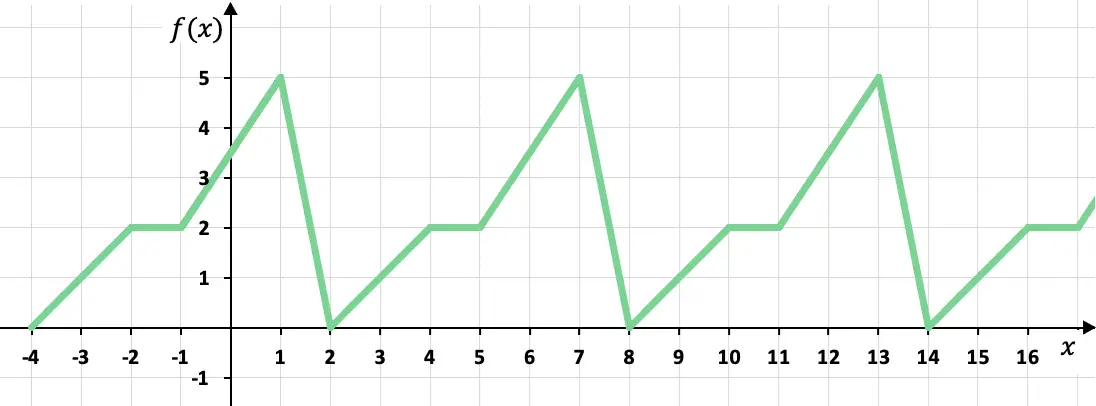
Bu parçalı tanımlı fonksiyon, grafiğinin değerleri döngüsel olarak tekrarlandığından periyodik bir fonksiyondur. Daha doğrusu fonksiyon her altı x’te aynı değeri alır, dolayısıyla fonksiyonun periyodu 6’ya eşittir.
![]()
Örnek 2
Aşağıdaki fonksiyonun periyodikliğini bulun:
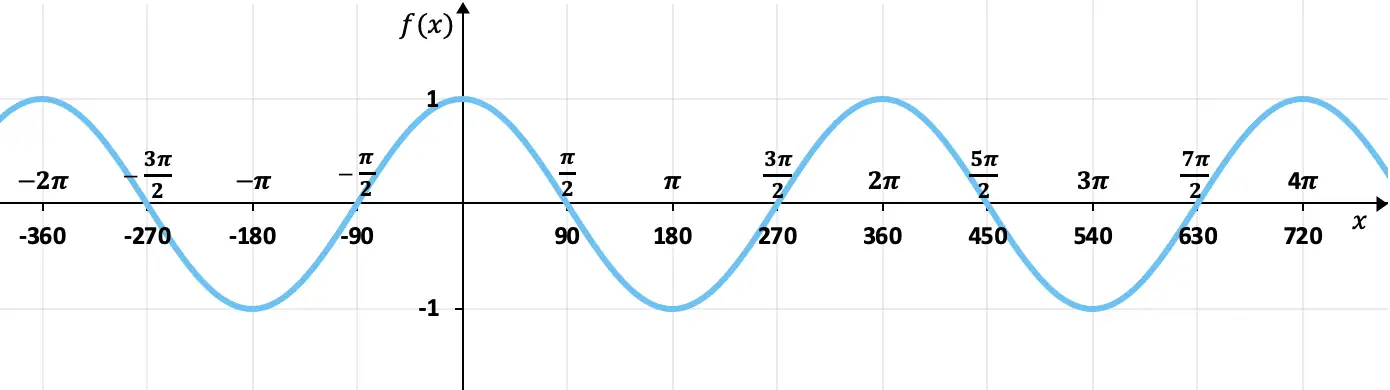
Bu fonksiyon, trigonometrik bir fonksiyonun, daha doğrusu kosinüs fonksiyonunun grafik temsiline karşılık gelir.
Grafikten de görebileceğimiz gibi fonksiyon değerlerini periyodik olarak tekrarlıyor yani periyodik bir fonksiyondur. Ek olarak, dalganın tepe noktası ile tepe noktası arasında 2π (veya 360°) boşluk vardır, dolayısıyla bu, fonksiyonun periyodudur.
![]()
Trigonometrik fonksiyonların periyodikliği
Periyodiklik ve trigonometrik fonksiyonlar yakından ilişkilidir, aslında bu tür fonksiyonların temel özelliklerinden biri trigonometrik fonksiyonların çoğunun periyodik olmasıdır.
Daha sonra 3 ana trigonometrik fonksiyonun periyodikliğini inceleyeceğiz: sinüs, kosinüs ve tanjant.
Sinüs fonksiyon periyodu
Sinüs fonksiyonunun ifadesi aşağıdaki gibidir:
![]()
Bu durumda, periyodunu bulmak için fonksiyonun grafiğini çizmeye gerek yoktur, ancak aşağıdaki formül uygulanarak basitçe hesaplanabilir:
![]()
Ek olarak sinüs fonksiyonunun özelliği, periyodunu değiştirirsek grafiğinin şeklini de değiştirmemizdir. Dönem değerinin grafik gösterimini nasıl etkilediğini aşağıdaki bağlantıdan görebilirsiniz:
➤ Bakınız: Sinüs fonksiyonunun grafiği
Kosinüs fonksiyonunun periyodu
Kosinüs fonksiyonunun cebirsel ifadesi aşağıdaki gibidir:
![]()
Sinüsde olduğu gibi kosinüs fonksiyonunun periyodu doğrudan aşağıdaki formül kullanılarak bulunabilir:
![]()
Kosinüs periyodunun değeri tamamen grafiğini belirler, aşağıdaki bağlantıya tıklayın ve nedenini öğrenin:
➤ Bakınız: Kosinüs fonksiyonunun grafiği
Teğet fonksiyonunun periyodu
Teğet fonksiyonu matematiksel olarak tanımlanır:
![]()
Teğet fonksiyonunun periyodu sinüs ve kosinüs ile aynı formülle hesaplanır:
![]()
Ancak teğet fonksiyon grafiği sinüs ve kosinüs grafiklerinden farklıdır çünkü periyodik olarak tekrarlanan asimptotlara da sahiptir. Bu trigonometrik fonksiyonun bunu ve diğer özelliklerini aşağıdaki bağlantıda görebilirsiniz:
➤ Bakınız: Teğet fonksiyonunun grafiği