Fonksiyonların temsili -

Bu yazıda herhangi bir fonksiyonun grafik üzerinde nasıl temsil edileceğini göreceğiz. Ek olarak, fonksiyonların grafik üzerinde temsil edilmesine ilişkin adım adım çözülmüş alıştırmalar bulacaksınız.

Bir fonksiyon grafikte nasıl temsil edilir?

Bir fonksiyonu grafik üzerinde temsil etmek için aşağıdaki adımlar gerçekleştirilmelidir:

Fonksiyonun tanım kümesini bulun.
Fonksiyonun kesme noktalarını Kartezyen eksenlerle hesaplayın.
Fonksiyonun asimptotlarını hesaplayın.
Fonksiyonun monotonluğunu inceleyin ve göreceli uç noktalarını bulun.
Fonksiyonun eğriliğini inceleyin ve dönüm noktalarını bulun.
Kesme noktalarını, asimptotları, bağıl ekstremumları ve dönüm noktalarını çizin , ardından fonksiyonu çizin.

Bir işlevi temsil etme örneği

Bir fonksiyonun grafiksel olarak nasıl temsil edildiğini görebilmeniz için aşağıdaki alıştırmayı adım adım çözeceğiz:

Aşağıdaki rasyonel fonksiyonu bir grafik üzerinde çizin:

$f(x)=\cfrac{x^2}{x-1}$

Yapılacak ilk şey fonksiyonun tanım kümesini hesaplamaktır . Bu rasyonel bir fonksiyondur, dolayısıyla hangi sayıların fonksiyonun tanım kümesine ait olmadığını görmek için paydayı sıfıra eşitlememiz gerekir:

$x-1=0$

$x=1$

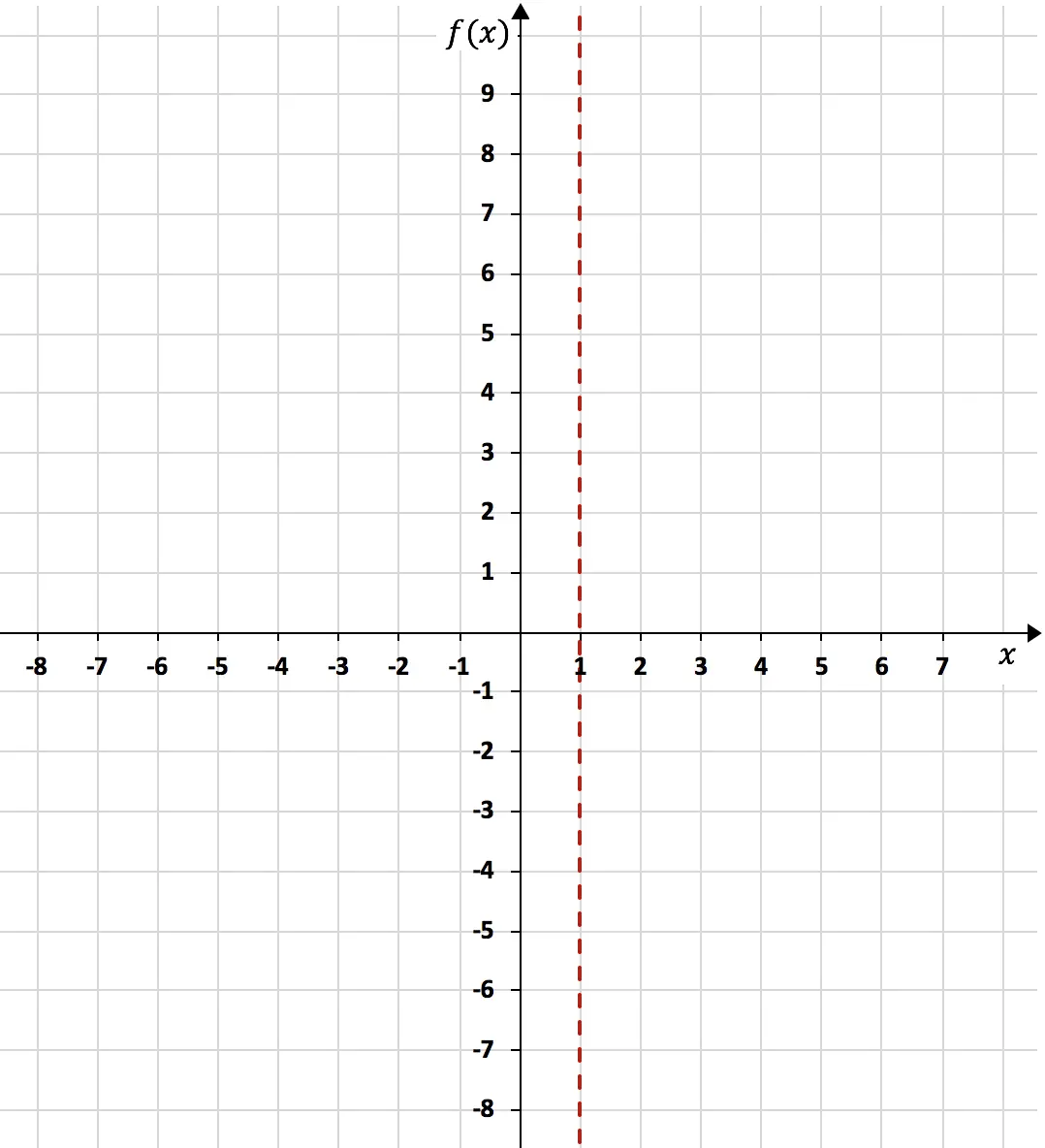
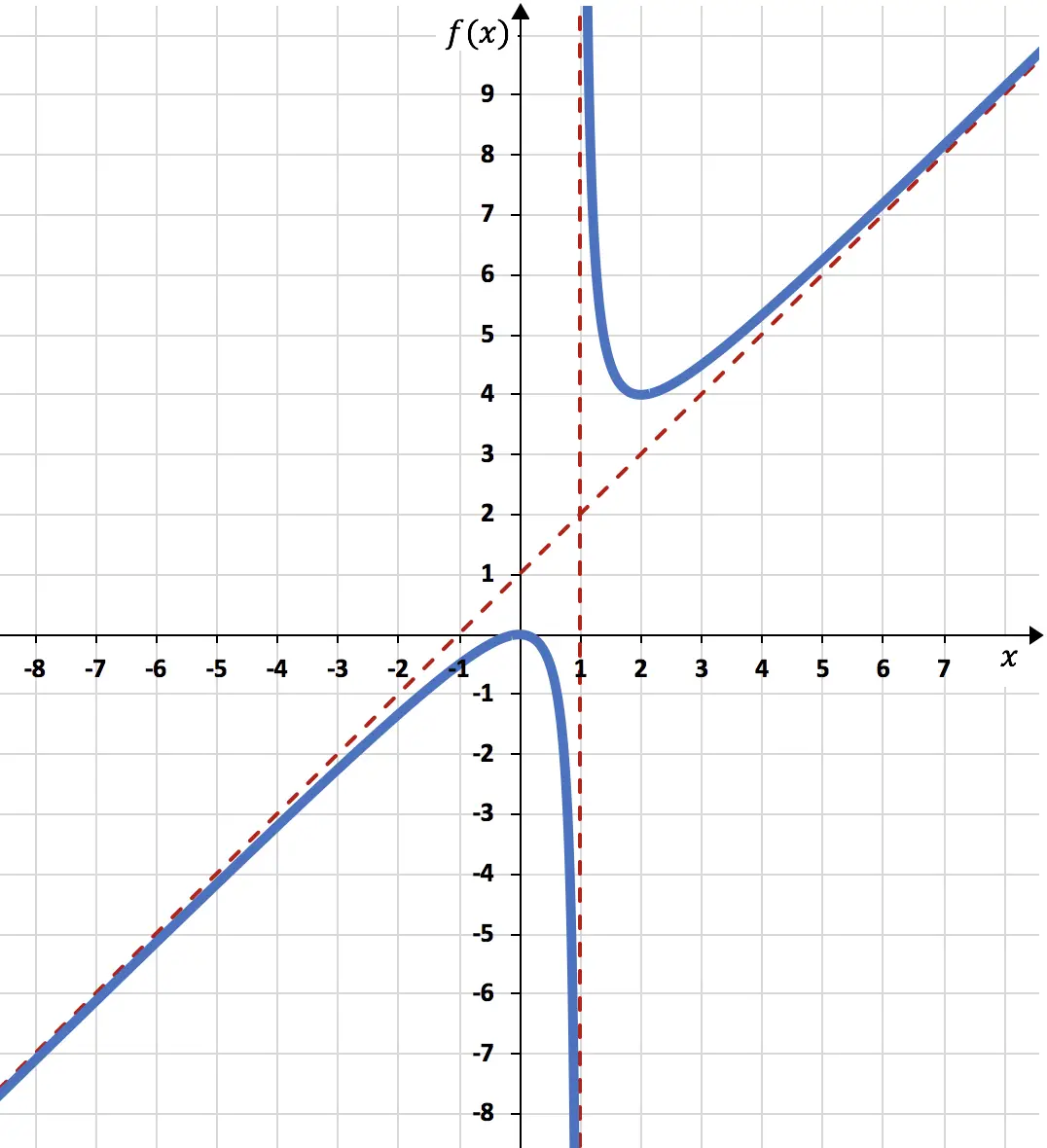
Yani x 1 olduğunda payda 0 olacak ve dolayısıyla fonksiyon mevcut olmayacaktır. Dolayısıyla fonksiyonun tanım kümesi x=1 dışındaki tüm gerçek sayılardan oluşur.

$\text{Dom } f= \mathbb{R}-\{1 \}$

X ekseni ile kesişme noktasını bulmak için denklemi çözmeliyiz

$f(x)= 0.$

Fonksiyonun X ekseninde değeri her zaman 0 olduğundan:

$f(x)=0$

$\cfrac{x^2}{x-1} = 0$

Dönem

$x -1$

Bu, sol tarafın tamamını bölmeyi içerir, böylece bunu sağ tarafın tamamıyla çarpabiliriz:

$x^2 = 0 \cdot (x-1)$

$x^2 = 0$

$x = 0$

Dolayısıyla OX ekseniyle kesişme noktası şu şekildedir:

$\bm{(0,0)}$

Ve Y ekseniyle kesişme noktasını bulmak için şunu hesaplıyoruz:

$f(0).$

Çünkü x, Y ekseninde her zaman 0’dır:

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0$

Bu nedenle OY ekseni ile kesme noktası:

$\bm{(0,0)}$

Bu durumda fonksiyon koordinat orijininden geçtiğinde X ekseni ile kesişme noktası Y ekseni ile kesişme noktası ile çakışır.

Tanım kümesini ve kesme noktalarını öğrendikten sonra fonksiyonun asimptotlarını hesaplamamız gerekir.

Fonksiyonun düşey asimptotlara sahip olup olmadığını görmek için fonksiyonun tanım kümesine ait olmayan noktalardaki limitini (bu durumda x=1) hesaplamamız gerekir. Ve eğer sonuç sonsuzsa bu dikey bir asimptottur. Henüz:

$\displaystyle \lim_{x \to 1} \ \cfrac{x^2}{x-1} = \cfrac{1^2}{1-1} = \cfrac{1}{0} = \infty$

Fonksiyonun x’in 1’e yöneldiği andaki limiti sonsuzluğu verdiğinden, x=1 dikey bir asimptottur:

fonksiyonları temsil eder, dikey asimptot

Düşey asimptot hesaplandıktan sonra fonksiyonun yanal limitlerinin buna göre hesaplanması gerekir. Çünkü fonksiyonun x=1’e soldan yaklaşırken -∞’a mı yoksa +∞’ya mı yöneleceğini bilmediğimiz gibi, x=1’e sağdan yaklaştığında da bilmiyoruz.

Böylece fonksiyonun x=1 noktasında sol yanal limitini hesaplamaya devam ediyoruz:

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1}$

Bir noktadaki yan sınırı sayısal olarak hesaplamak için, fonksiyona o noktaya çok yakın bir sayı koymamız gerekir. Bu durumda solda 1’e çok yakın, 0,9 gibi bir sayı istiyoruz. Bu nedenle fonksiyonda 0,9 noktasını değiştiririz:

$\cfrac{0,9^2}{0,9-1}=\cfrac{0,81}{-0,1}=-81$

Bir asimptotun yanal sınırları yalnızca +∞ veya -∞ verebilir. Ve fonksiyonda soldaki 1’e çok yakın bir sayıyı yerine koyduğumuzda negatif sonuç elde ettiğimiz için soldaki limit -∞ olur:

$\displaystyle \lim_{x \to 1^{-}} \cfrac{x^2}{x-1} = \bm{-\infty}$

Şimdi aynı işlemi sağ kenar sınırıyla da yapıyoruz:

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1}$

Sağdaki 1’e çok yakın bir sayıyı fonksiyona yerleştiriyoruz. Örneğin madde 1.1:

$\cfrac{1,1^2}{1,1-1}=\cfrac{1,21}{0,1}=+12,1$

Bu durumda yan limit sonucu pozitif bir sayıdır. Bu nedenle sağdaki limit +∞’dur:

$\displaystyle \lim_{x \to 1^{+}} \cfrac{x^2}{x-1} = \bm{+\infty}$

Sonuç olarak, x=1’de fonksiyon solda eksi sonsuza, sağda artı sonsuza doğru yönelir:

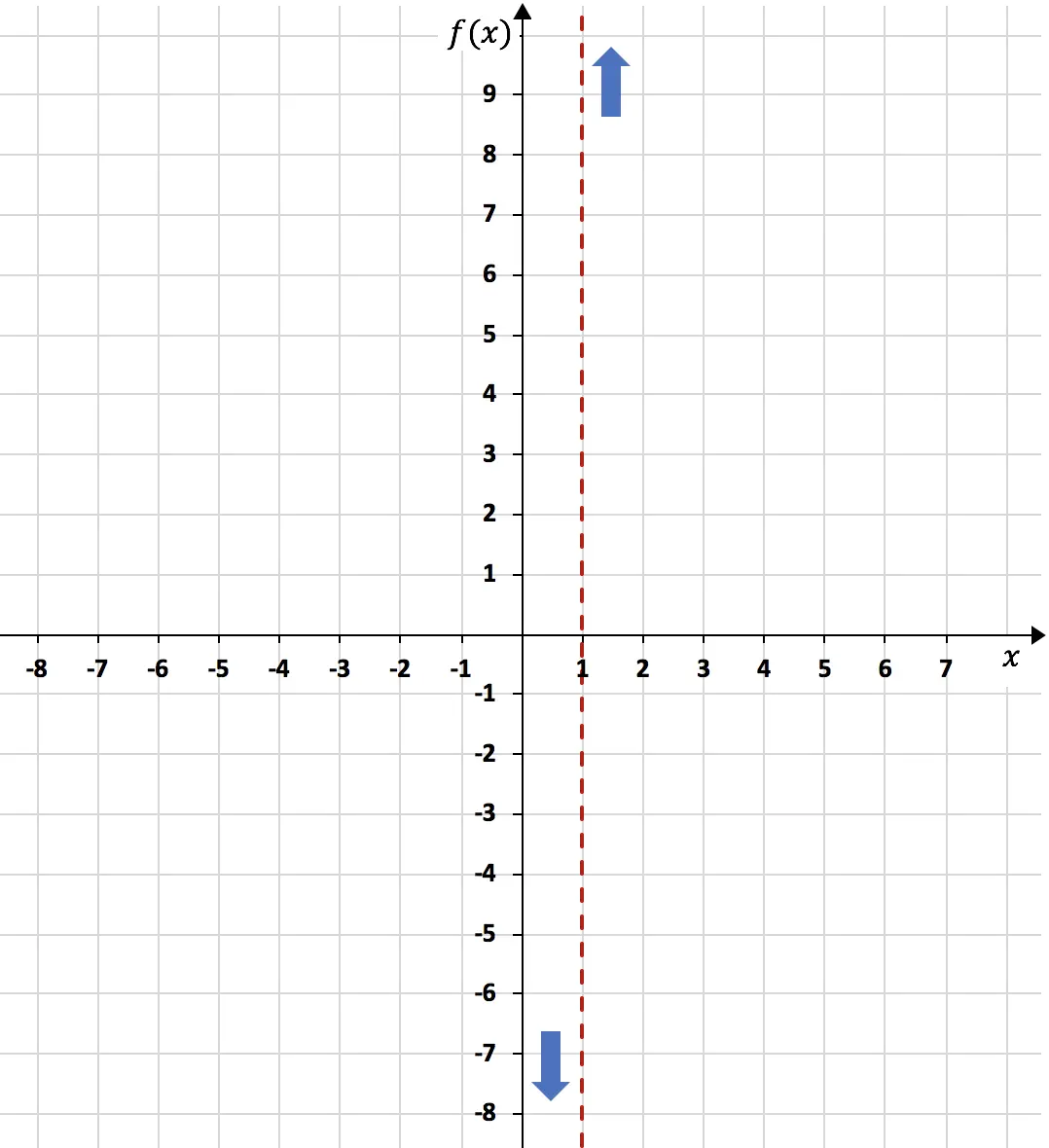
Öte yandan fonksiyonun yatay asimptotu fonksiyonun sonsuz limitinin sonucu olacaktır. Henüz:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2}{x-1} = \cfrac{+\infty}{+\infty } =+\infty$

Rasyonel fonksiyonların sonsuz limitlerini nasıl hesaplayacağınızı hatırlayın :

$\displaystyle \lim_{x \to \pm \infty}}\frac{a_nx^r+a_{n-1}x^{r-1}+a_{n-2}x^{r-2}+\dots}{b_nx^s+b_{n-1}x^{s-1}+b_{n-2}x^{s-2}+\dots}=\left\{ \begin{array}{lcl} 0 & \text{si} & r<s \\[3ex]="" \cfrac{a_n}{b_n}="" &="" \text{si}="" r="s" \\[5ex]="" \pm="" \infty="">s \end{array}\right.” title=”Rendered by QuickLaTeX.com” height=”139″ width=”767″ style=”vertical-align: 0px;”> </div> Fonksiyonun sonsuz limiti bize +∞ değerini verdi, dolayısıyla fonksiyonun yatay asimptotu yok. Şimdi eğik asimptotu hesaplıyoruz. Eğik asimptotlar şu şekildedir: <p class=$ $y=mx+n$

. VE

$m$

Aşağıdaki formülle hesaplanır:

$\displaystyle m = \lim_{x \to +\infty} f(x):x$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:x$

X sanki paydası 1miş gibi:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2}{x-1}:\cfrac{x}{1}$

Bu kesirlerin bölünmesidir, bu yüzden onları enine çarpıyoruz:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 \cdot 1 }{(x-1) \cdot x}$

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x}$

Ve limiti hesaplıyoruz:

$\displaystyle m = \lim_{x \to +\infty} \cfrac{x^2 }{x^2-x} = \cfrac{+\infty}{+\infty } = \cfrac{1}{1} = 1$

Yani m=1. Şimdi hesaplıyoruz

$n$

aşağıdaki formülle:

$\displaystyle n = \lim_{x \to +\infty} \bigl[f(x)-mx\bigr]$

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-1x\right] = \cfrac{+\infty}{+\infty} -(+\infty) = +\infty - \infty$

Ama belirsizlik sonsuz eksi sonsuzu elde ettiğimiz için terimleri ortak bir paydaya indirgememiz gerekiyor. Bunu yapmak için x terimini kesrin paydasıyla çarpıp bölüyoruz:

$\displaystyle n = \lim_{x \to +\infty}\left[\cfrac{x^2}{x-1}-x\right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x\cdot (x-1)}{x-1} \right] = \lim_{x \to +\infty} \left[\cfrac{x^2}{x-1}-\cfrac{x^2-x}{x-1}\right]$

Artık iki terim aynı paydaya sahip olduğuna göre bunları gruplandırabiliriz:

$\displaystyle n = \lim_{x \to +\infty} \left[\cfrac{x^2-(x^2-x)}{x-1} \right] =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right]$

Ve son olarak limiti çözüyoruz:

$\displaystyle n =\lim_{x \to +\infty} \left[\cfrac{x}{x-1} \right] = \cfrac{+\infty}{+\infty} = \cfrac{1}{1} = 1$

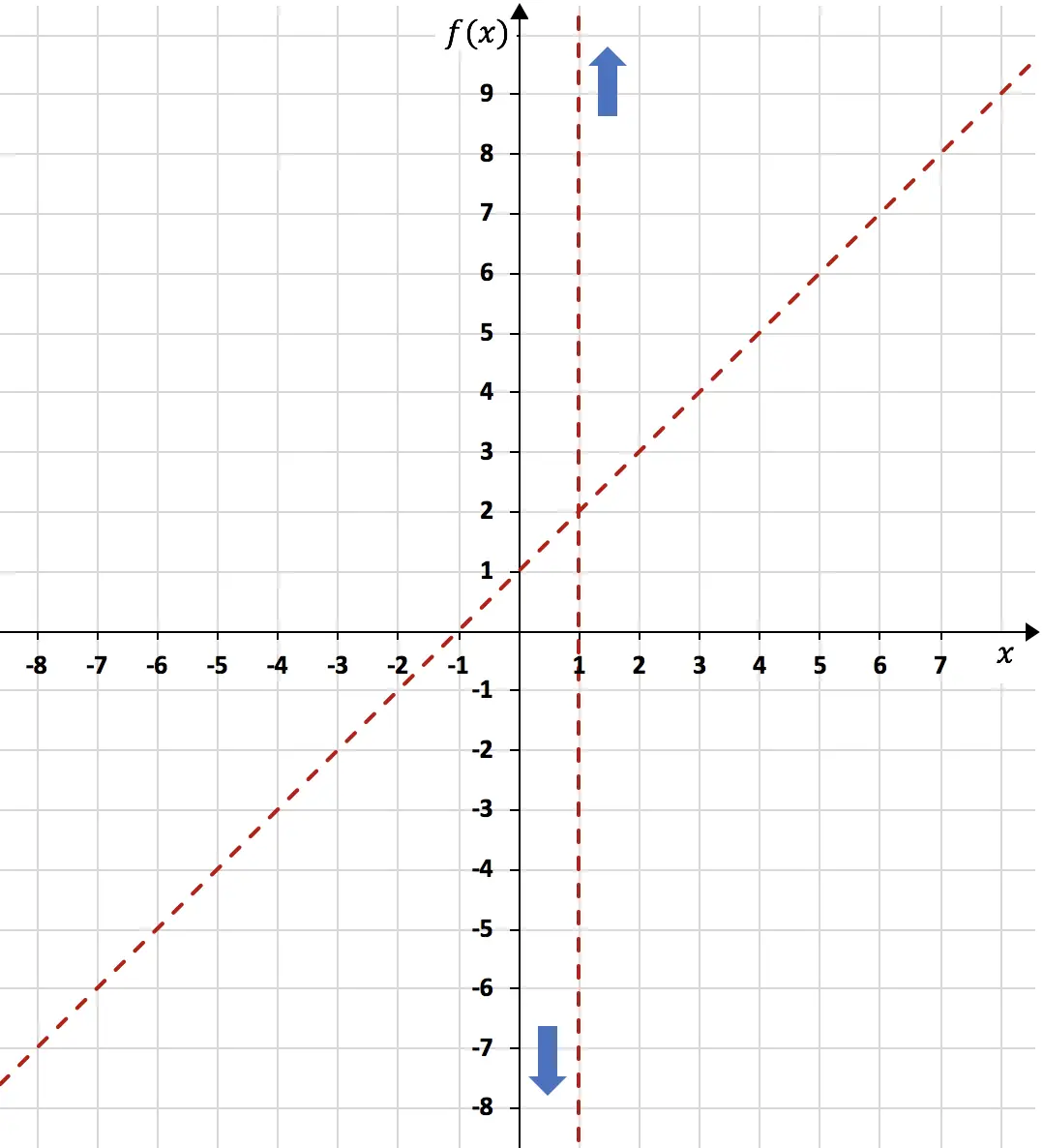
Yani n = 1. Dolayısıyla eğik asimptot şu şekildedir:

$y = mx+n$

$y = 1x+1$

$\bm{y = x+1}$

Eğik asimptotu hesapladıktan sonra onu aynı grafik üzerinde bir değerler tablosu oluşturarak temsil ederiz:

$y=x+1$

$\begin{array}{c|c} x & y \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \end{array}$

fonksiyonları temsil eder, eğik asimptot

Artık fonksiyonun tüm asimptotlarını bildiğimize göre fonksiyonun monotonluğunu analiz etmemiz gerekiyor. Yani fonksiyonun hangi aralıklarda arttığını, hangi aralıklarda azaldığını araştırmamız gerekiyor. Bu nedenle fonksiyonun birinci türevini hesaplıyoruz:

$f(x)=\cfrac{x^2}{x-1} \ \longrightarrow \ f'(x)= \cfrac{2x\cdot (x-1) - x^2 \cdot 1}{(x-1)^2}$

$f'(x)= \cfrac{2x^2-2x - x^2}{(x-1)^2} = \cfrac{x^2-2x}{(x-1)^2}$

Şimdi türevi 0’a eşitliyoruz ve denklemi çözüyoruz:

$f'(x)=0$

$\cfrac{x^2-2x}{(x-1)^2}=0$

Dönem

$\left(x-1\right)^2}$

Bu, sol tarafın tamamını bölmeyi içerir, böylece bunu sağ tarafın tamamıyla çarpabiliriz:

$x^2-2x=0\cdot \left(x-1\right)^2$

$x^2-2x=0$

İkinci dereceden denklemi çözmek için ortak faktörü çıkarıyoruz:

$x(x-2)=0$

Çarpmanın 0’a eşit olması için çarpımın iki unsurundan birinin sıfır olması gerekir. Bu nedenle, her faktörü 0’a eşitliyoruz ve denklemin her iki çözümünü de elde ediyoruz:

$\displaystyle x\cdot(x-2) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] x-2=0 \ \longrightarrow \ \bm{x= 2} \end{cases}$

Şimdi bulunan tüm kritik noktaları, yani tanım kümesine ait olmayan noktaları (x=1) ve türevi iptal eden noktaları (x=0 ve x=2) sayı doğrusunda temsil ediyoruz:

Ve fonksiyonun arttığını mı yoksa azaldığını mı bilmek için her aralıkta türevin işaretini değerlendiririz. Bu nedenle her aralıkta bir nokta alıyoruz (asla kritik noktaları değil) ve türevin o noktada hangi işarete sahip olduğuna bakıyoruz:

$f'(x)=\cfrac{x^2-2x}{\left(x-1\right)^2}$

$f'(-1) = \cfrac{(-1)^2-2(-1)}{\left((-1)-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

$f'(0,5) = \cfrac{0,5^2-2\cdot 0,5}{\left(0,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(1,5) = \cfrac{1,5^2-2\cdot 1,5}{\left(1,5-1\right)^2} = \cfrac{-0,75}{+0,25} = -3 \ \rightarrow \ \bm{-}$

$f'(3) = \cfrac{3^2-2\cdot 3}{\left(3-1\right)^2} =\cfrac{+3}{+4} = +0,75 \ \rightarrow \ \bm{+}$

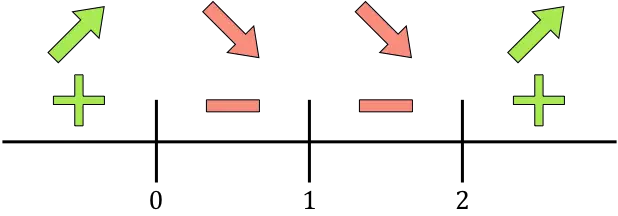
Türev pozitifse fonksiyon artıyor, türev negatifse fonksiyon azalıyor demektir. Buna göre büyüme ve düşüş aralıkları şöyledir:

Büyüme:

$\bm{(-\infty, 0)\cup (2,+\infty)}$

Azaltmak:

$\bm{(0,1)\cup (1,2)}$

Ayrıca, x=0’da fonksiyon artandan azalan tarafa doğru gider, dolayısıyla x=0 fonksiyonun göreceli maksimumudur. Ve x=2’de fonksiyon azalan durumdan artana doğru gider, yani x=2 fonksiyonun göreceli minimumudur.

Son olarak, noktaların Y koordinatını bulmak için bulunan uç noktaları orijinal fonksiyonda yerine koyarız:

$f(0)=\cfrac{0^2}{0-1} = \cfrac{0}{-1} = 0 \ \longrightarrow \ (0,0)$

$f(2)=\cfrac{2^2}{2-1} = \cfrac{4}{1} = 4 \ \longrightarrow \ (2,4)$

Dolayısıyla fonksiyonun göreceli ekstremleri şöyledir:

Maksimum nokta

$\bm{(0,0)}$

Minimum noktaya

$\bm{(2,4)}$

Grafikte maksimum ve minimum değerleri temsil ediyoruz:

maksimum ve minimum fonksiyonları temsil eder

Son olarak fonksiyonun eğriliğini incelemek , yani fonksiyonun içbükeylik ve dışbükeylik aralıklarını incelemek yeterlidir. Bunu yapmak için ikinci türevini hesaplıyoruz:

$f'(x)=\cfrac{x^2-2x}{(x-1)^2} \ \longrightarrow \ f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)\cdot 1}{\left(\left(x-1\right)^2\right)^2}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^2- (x^2-2x)\cdot 2(x-1)}{(x-1)^4}$

$f''(x)= \cfrac{(2x-2)\cdot (x-1)^{\cancel{2}}- (x^2-2x)\cdot 2\cancel{(x-1)}}{(x-1)^{\cancelto{3}{4}}} = \cfrac{(2x-2)\cdot (x-1)- (x^2-2x)\cdot 2}{(x-1)^3}$

$f''(x)= \cfrac{2x^2-2x-2x+2- (2x^2-4x)}{(x-1)^3} =\cfrac{2x^2-2x-2x+2- 2x^2+4x}{(x-1)^3}$

$f''(x) =\cfrac{2}{(x-1)^3}$

Şimdi ikinci türevi sıfıra eşitliyoruz ve denklemi çözüyoruz:

$f''(x)=0$

$\cfrac{2}{(x-1)^3} =0$

$2=0\cdot \left(x-1\right)^3$

$2=0$

2 asla 0’a eşit olmayacak, dolayısıyla denklem

$f''(x)=0$

Çözümü yok.

Şimdi bulunan tüm kritik noktaları, yani tanım kümesine ait olmayan (x=1) ve ikinci türevi iptal eden noktaları (bu durumda olmayan yoktur) sayı doğrusunda temsil ediyoruz:

Fonksiyonun dışbükey mi yoksa içbükey mi olduğunu bilmek için her aralıkta türevin işaretini değerlendiririz. Bu nedenle her aralıkta bir nokta alıyoruz (asla tekil noktalar değil) ve türevin bu noktada hangi işarete sahip olduğuna bakıyoruz:

$f''(x) =\cfrac{2}{(x-1)^3}$

$f''(0) =\cfrac{2}{(0-1)^3} = \cfrac{2}{-1}=-2 \ \rightarrow \ \bm{-}$

$f''(2) =\cfrac{2}{(2-1)^3} = \cfrac{2}{1}=2 \ \rightarrow \ \bm{+}$

Ve son olarak fonksiyonun içbükeylik ve dışbükeylik aralıklarını çıkarıyoruz. İkinci türevin pozitif olması fonksiyonun dışbükey olduğu anlamına gelir.

$(\bm{\cup})$

ve ikinci türev negatifse bu, fonksiyonun içbükey olduğu anlamına gelir

$(\bm{\cap})$

. Bu nedenle içbükeylik ve dışbükeylik aralıkları şöyledir:

Dışbükey

$(\bm{\cup})$

$\bm{(1,+\infty)}$

İçbükey

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Ancak x=1 noktasında eğrilikte değişiklik olsa da bu bir dönüm noktası değildir. Çünkü x=1 fonksiyonun tanım kümesine ait değildir.

Böylece hesapladığımız her şeyi kullanarak işlevi temsil etmeyi bitirebiliriz:

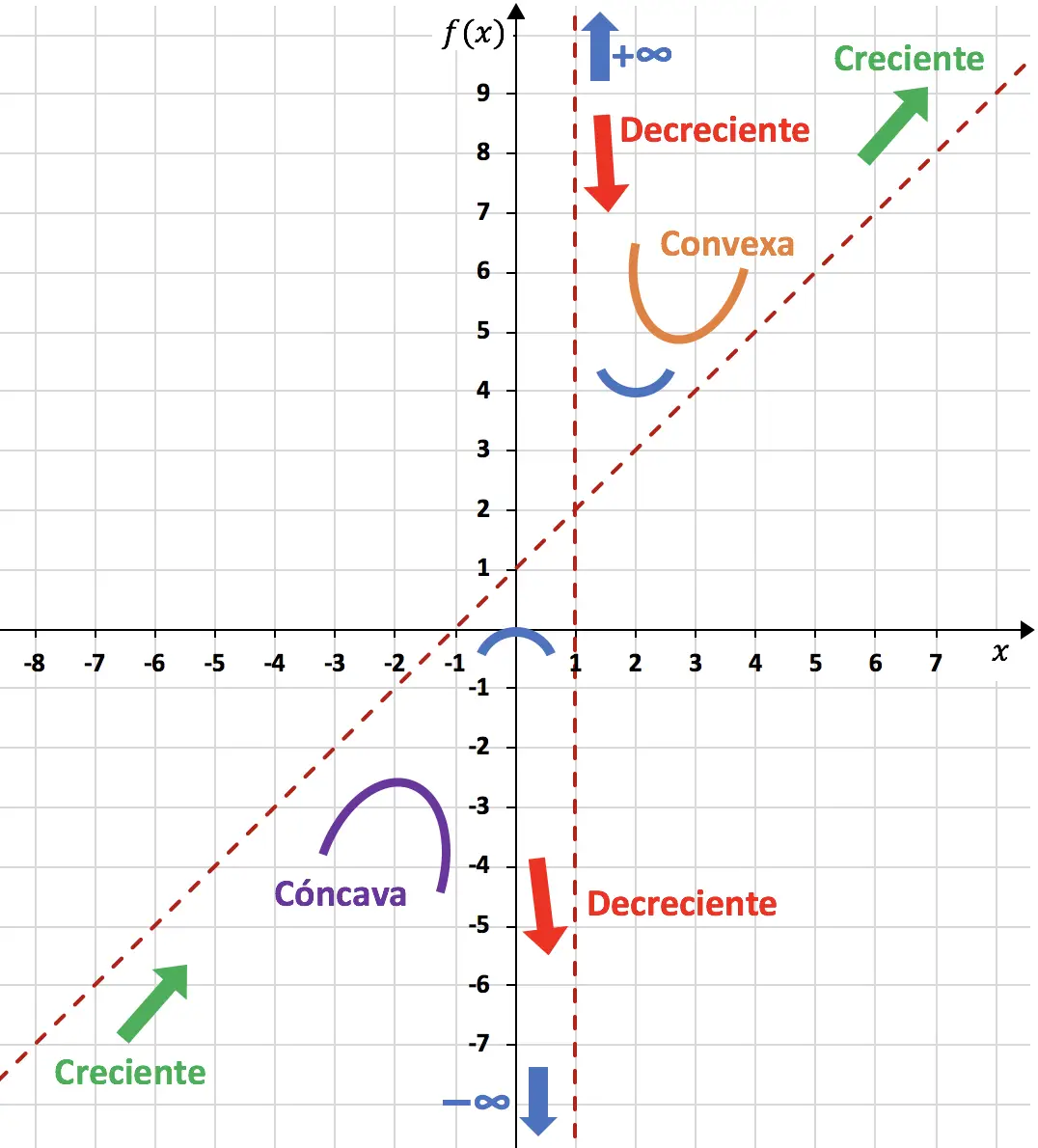
Dolayısıyla grafikte temsil edilen fonksiyon şuna benzer:

rasyonel fonksiyonun grafiksel gösterimi

Fonksiyonları temsil etmeye yönelik çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki polinom fonksiyonunun grafiğini çizin:

$\displaystyle f(x)=x^3-3x^2+4$

Çözümü görün

Yapılacak ilk şey fonksiyonun tanım tanım kümesini hesaplamaktır. Bu bir polinom fonksiyonudur, dolayısıyla etki alanı yalnızca gerçek sayılardan oluşur:

$\text{Dom } f= \mathbb{R}$

X ekseni ile kesişme noktasını bulmak için çözüyoruz

$f(x)= 0.$

$f(x)=0$

$x^3-3x^2+4=0$

Bu, 2’den büyük bir derece denklemidir. Bu nedenle denklemi çarpanlarına ayırıyoruz:

$(x+1)(x^2-4x+4)=0$

Yani x=-1 bir çözümdür. Ve elde edilen ikinci dereceden denklemi çözerek diğer çözümleri hesaplıyoruz:

$\begin{aligned}x & =\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} =\cfrac{-(-4) \pm \sqrt{(-4)^2-4\cdot 1 \cdot 4}}{2\cdot 1} \\[2ex] &=\cfrac{+4 \pm \sqrt{16-16}}{2} =\cfrac{4 \pm \sqrt{0}}{2} = \cfrac{4 }{2 } = 2\end{aligned}$

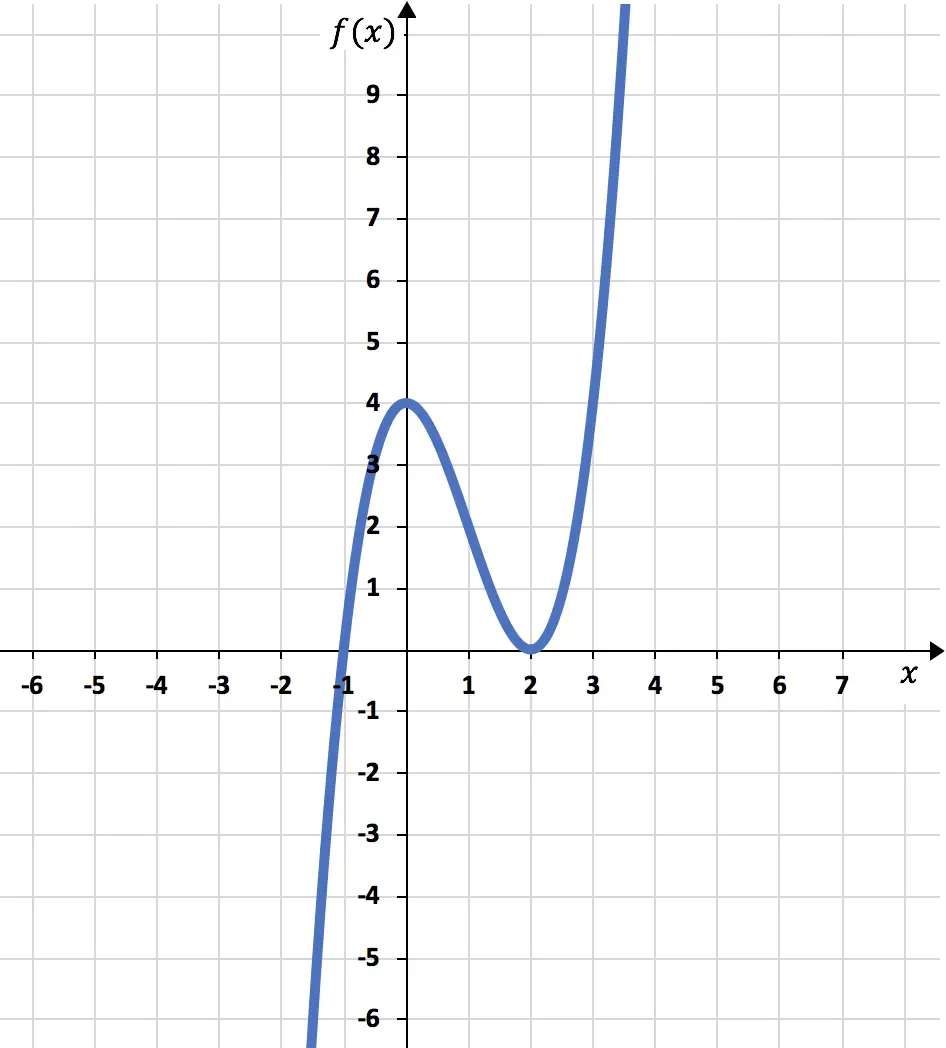
Dolayısıyla X ekseni ile kesişme noktaları şunlardır:

$\bm{(-1,0)}$

$\bm{(2,0)}$

Y ekseniyle kesişme noktasını bulmak için şunu hesaplıyoruz:

$f(0).$

Y ekseninde x her zaman 0 olduğundan:

$f(0)=0^3-3\cdot0^2+4 = 4$

Dolayısıyla Y ekseniyle kesişme noktası şu şekildedir:

$\bm{(0,4)}$

Fonksiyonun düşey asimptotlara sahip olup olmadığını görmek için fonksiyonun tanım kümesine ait olmayan noktalardaki limitini hesaplamamız gerekir. Bu durumda etki alanı tüm gerçek sayıları içerir. Dolayısıyla fonksiyonun dikey asimptotu yoktur.

Öte yandan fonksiyonun yatay asimptotu fonksiyonun sonsuz limitinin sonucu olacaktır. Henüz:

$\displaystyle \lim_{x \to +\infty} \ x^3-3x^2+4 =(+\infty)^3 = +\infty$

Fonksiyonun sonsuz limiti bize +∞ değerini verdi, dolayısıyla fonksiyonun yatay asimptotu yok.

Şimdi eğik asimptotu hesaplıyoruz. Eğik asimptotlar şu şekildedir:

$y=mx+n.$

$m$

Aşağıdaki formülle hesaplanır:

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \left( x^3-3x^2+4\right): x =$

$\displaystyle = \lim_{x \to +\infty} \cfrac{x^3-3x^2+4}{x} = \cfrac{+\infty}{+\infty} = +\infty$

Limit bize +∞ değerini verdi, dolayısıyla fonksiyonun eğik asimptotu da yok.

Fonksiyonun monotonluğunu incelemek için önce türevini hesaplamalıyız:

$f(x)= x^3-3x^2+4 \ \longrightarrow \ f'(x)= 3x^2-6x$

Şimdi türevi 0’a eşitliyoruz ve denklemi çözüyoruz:

$f'(x)= 0$

$3x^2-6x=0$

$x(3x-6)=0$

$\displaystyle x\cdot(3x-6) =0 \longrightarrow \begin{cases} \bm{x=0} \\[2ex] 3x-6=0 \ \longrightarrow \ x= \cfrac{6}{3} = 2 \end{cases}$

Şimdi elde edilen tüm tekil noktaları, yani tanım kümesine ait olmayan noktaları (bu durumda hepsi aittir) ve türevi iptal eden noktaları (x=0 ve x =2) sayı doğrusu üzerinde temsil ediyoruz. :

Ve fonksiyonun arttığını mı yoksa azaldığını mı bilmek için her aralıkta türevin işaretini değerlendiririz. Bu nedenle her aralıkta bir nokta alıyoruz (asla tekil noktalar değil) ve türevin bu noktada hangi işarete sahip olduğuna bakıyoruz:

$f'(-1)=3(-1)^2-6(-1)= 3+6 = 9\ \rightarrow \ \bm{+}$

$f'(1)=3\cdot 1^2-6\cdot 1= 3-6 = -3\ \rightarrow \ \bm{-}$

$f'(3)=3\cdot 3^2-6\cdot 3= 27-18 = 9\ \rightarrow \ \bm{+}$

Türev pozitifse fonksiyon artıyor, türev negatifse fonksiyon azalıyor demektir. Buna göre büyüme ve düşüş aralıkları şöyledir:

Büyüme:

$\bm{(-\infty,0)\cup (2,+\infty)}$

Azaltmak:

$\bm{(0,2)}$

Fonksiyon x=0’da artandan azalana doğru gider, dolayısıyla x=0 fonksiyonun maksimumudur. Ve fonksiyon x=2’de azalmadan artmaya doğru gidiyor, yani x=2 fonksiyonun minimumu.

Son olarak, noktaların Y koordinatlarını bulmak için bulunan uç noktaları orijinal fonksiyonda yerine koyarız:

$f(0)=0^3-3\cdot 0^2+4 = 4 \ \longrightarrow \ (0,4)$

$f(2)=2^3-3\cdot 2^2+4 = 8-3 \cdot 4 +4 = 0 \ \longrightarrow \ (2,0)$

Dolayısıyla fonksiyonun göreceli ekstremleri şöyledir:

Maksimum nokta

$\bm{(0,4)}$

Minimum noktaya

$\bm{(2,0)}$

Fonksiyonun eğriliğini incelemek için ikinci türevini hesaplıyoruz:

$f'(x)= 3x^2-6x \ \longrightarrow \ f''(x)= 6x-6$

Şimdi ikinci türevi 0’a eşitliyoruz ve denklemi çözüyoruz:

$f''(x)= 0$

$6x-6=0$

$6x=6$

$x= \cfrac{6}{6} = 1$

Bulunan tüm tekil noktaları, yani tanım kümesine ait olmayan noktaları (bu durumda hepsi aittir) ve türevi (x=1) götüren noktaları doğru üzerinde temsil ederiz:

Şimdi fonksiyonun içbükey mi yoksa dışbükey mi olduğunu bilmek için her aralıkta ikinci türevin işaretini değerlendireceğiz. Bu nedenle her aralıkta bir nokta alıyoruz (asla tekil noktaları değil) ve bu noktada ikinci türevin hangi işarete sahip olduğuna bakıyoruz:

$f''(0)=6\cdot 0-6= -6 \ \rightarrow \ \bm{-}$

$f''(2)=6\cdot 2-6= 12-6= 6 \ \rightarrow \ \bm{+}$

İkinci türevin pozitif olması fonksiyonun dışbükey olduğu anlamına gelir.

$(\bm{\cup})$

ve ikinci türev negatifse bu, fonksiyonun içbükey olduğu anlamına gelir

$(\bm{\cap})$

. Bu nedenle içbükeylik ve dışbükeylik aralıkları şöyledir:

Dışbükey

$(\bm{\cup})$

$\bm{(1,+\infty)}$

İçbükey

$(\bm{\cap})$

$\bm{(-\infty,1)}$

Ek olarak, fonksiyon x=1’de içbükeyden dışbükeye değişir, dolayısıyla x=1, fonksiyonun bir dönüm noktasıdır.

Son olarak, noktaların Y koordinatını bulmak için bulunan dönüm noktalarını orijinal fonksiyonda yerine koyarız:

$f(1)=1^3-3\cdot 1^2+ 4= 1 -3 +4 =2 \ \longrightarrow \ (1,2)$

Dolayısıyla fonksiyonun dönüm noktaları şunlardır:

Dönüş noktası:

$\bm{(1,2)}$

Son olarak hesapladığımız tüm bilgilere dayanarak fonksiyonun grafiğini çizeriz:

polinom fonksiyonunun grafiksel gösterimi

Alıştırma 2

Aşağıdaki rasyonel fonksiyonun grafiğini çizin:

$\displaystyle f(x)=\frac{x^2+2}{x^2-1}$

Çözümü görün

Fonksiyonun tanım kümesini bulmak için paydayı eşitleriz. kesri sıfıra getirin ve elde edilen denklemi çözün:

$x^2-1= 0$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm 1$

$\text{Dom } f= \mathbb{R}-\{-1, +1 \}$

İkinci olarak, x ekseni fonksiyonun cebirsel ifadesine eşit olacak şekilde fonksiyonun eşiklerini belirliyoruz. çelik:

$f(x)=0$

$\cfrac{x^2+2}{x^2-1}=0$

$x^2+2=0\cdot (x^2-1)$

$x^2+2=0$

$x^2=-2$

$x=\sqrt{-2} \quad \color{red}\bm{\times}$

Negatif bir sayının karekökü yoktur. Bu nedenle fonksiyon X eksenini kesmez.

Bilgisayar ekseniyle kesişme noktasını bulmak için fonksiyonu x=0’da hesaplıyoruz.

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2$

Dolayısıyla Y ekseniyle kesişme noktası şu şekildedir:

$\bm{(0,-2)}$

Fonksiyonun dikey asimptotları olup olmadığını görmek için, fonksiyonun tanım kümesine ait olmayan noktalardaki limitini hesaplamamız gerekir (bu durumda x=-1 ve x=+1). Ve eğer sonuç sonsuzsa bu dikey bir asimptottur. Henüz:

$\displaystyle \lim_{x \to -1} \cfrac{x^2+2}{x^2-1} = \cfrac{(-1)^2+2}{(-1)^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

x -1’e yaklaşırken fonksiyonun limiti sonsuzluk verdiğinden, x=-1 dikey bir asimptottur.

Asimptot x=-1’in yanal sınırlarını, ona çok yakın bir sayıyı fonksiyonda değiştirerek hesaplıyoruz:

$\displaystyle f(-1,1)=\cfrac{(-1,1)^2+2}{(-1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to -1^{-}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

$\displaystyle f(-0,9)=\cfrac{(-0,9)^2+2}{(-0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to -1^{+}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

Şimdi x=+1’in dikey bir asimptot olup olmadığına bakalım:

$\displaystyle \lim_{x \to +1} \cfrac{x^2+2}{x^2-1} = \cfrac{1^2+2}{1^2-1} =\cfrac{1+2}{1-1}= \cfrac{3}{0} = \infty$

x +1’e yaklaşırken fonksiyonun limiti sonsuzluk verdiğinden, x=+1 dikey bir asimptottur.

Asimptot x=1’in yanal sınırlarını, ona çok yakın bir sayıyı fonksiyonda değiştirerek hesaplıyoruz:

$\displaystyle f(0,9)=\cfrac{(0,9)^2+2}{(0,9)^2-1} =-14,79 \longrightarrow \lim_{x \to +1^{-}} \ \cfrac{x^2+2}{x^2-1} = -\infty$

$\displaystyle f(1,1)=\cfrac{(1,1)^2+2}{(1,1)^2-1} =+15,29 \longrightarrow \lim_{x \to +1^{+}} \ \cfrac{x^2+2}{x^2-1} = +\infty$

Öte yandan fonksiyonun yatay asimptotu fonksiyonun sonsuz limitinin sonucu olacaktır. Henüz:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^2+2}{x^2-1} = \cfrac{+\infty}{+\infty } =\cfrac{1}{1} = 1$

Fonksiyonun sonsuz limiti bize 1 değerini verdi, yani fonksiyonun y=1 noktasında yatay bir asimptotu var.

Fonksiyonun yatay bir asimptotu olduğundan eğik bir asimptotu olmayacaktır.

Fonksiyonu farklılaştırıyoruz, ardından büyüme ve azalma aralıklarını inceliyoruz:

$f(x)=\cfrac{x^2+2}{x^2-1} \ \longrightarrow \ f'(x)= \cfrac{2x \cdot (x^2-1) -(x^2+2) \cdot 2x}{\left(x^2-1 \right)^2}$

$f'(x)= \cfrac{2x^3-2x - (2x^3+4x) }{\left(x^2-1 \right)^2} = \cfrac{-6x}{\left(x^2-1 \right)^2}$

Şimdi türevi 0’a eşitliyoruz ve denklemi çözüyoruz:

$f'(x)= 0$

$\cfrac{-6x}{\left(x^2-1 \right)^2}=0$

$-6x=0\cdot\left(x^2-1 \right)^2$

$-6x= 0$

$x=\cfrac{0}{-6} = 0$

Hesaplanan tüm kritik noktaları (x=-1 ve x=+1) ve türevi iptal eden noktaları (x=0) doğru üzerinde temsil ediyoruz:

$f'(-2)= \cfrac{-6(-2)}{\left((-2)^2-1 \right)^2} = \cfrac{12}{9} =1,33 \ \rightarrow \ \bm{+}$

$f'(-0,5)= \cfrac{-6(-0,5)}{\left((-0,5)^2-1 \right)^2} = \cfrac{3}{0,56} =5,33 \ \rightarrow \ \bm{+}$

$f'(0,5)= \cfrac{-6\cdot 0,5}{\left(0,5^2-1 \right)^2} = \cfrac{-3}{0,56} =-5,33 \ \rightarrow \ \bm{-}$

$f'(2)= \cfrac{-6\cdot 2}{\left(2^2-1 \right)^2} = \cfrac{-12}{9} =-1,33 \ \rightarrow \ \bm{-}$

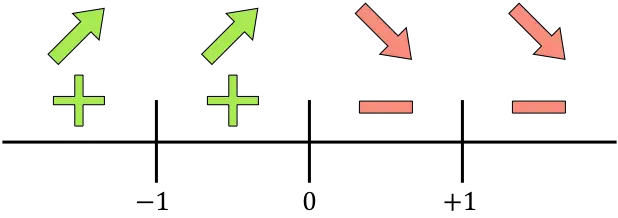
Türevin pozitif olduğu yerde fonksiyon artar, negatif olduğu yerde fonksiyon azalır:

Büyüme:

$\bm{(-\infty,-1)\cup (-1,0)}$

Azaltmak:

$\bm{(0,1)\cup (1,+\infty)}$

Fonksiyon x=0’da artıştan azalışa doğru gider, dolayısıyla x=0 fonksiyonun yerel maksimumudur.

Noktanın Y koordinatını bulmak için bulunan ekstremumu orijinal fonksiyonda yerine koyarız:

$f(0)=\cfrac{0^2+2}{0^2-1}= \cfrac{2}{-1} = -2 \ \longrightarrow \ (0,-2)$

Dolayısıyla fonksiyonun göreceli ekstremleri şöyledir:

Maksimum nokta

$\bm{(0,-2)}$

Fonksiyonun eğriliğini incelemek için ikinci türevini hesaplıyoruz:

$f'(x)=\cfrac{-6x}{\left(x^2-1 \right)^2} \ \longrightarrow <img src="https://mathority.org/wp-content/ql-cache/quicklatex.com-273969cf60ee8cf3413ee2f8b1db7688_l3.png" height="129" width="476" class="ql-img-displayed-equation quicklatex-auto-format" alt="\[f''(x)= \cfrac{-6 \cdot \left(x^2-1 \right)^2 - (-6x) \cdot 2(x^2-1) \cdot 2x}{ \left(\left(x^2-1 \right)^2\right)^2}$$ f''(x)= \cfrac{-6 \left(x^2-1 \right)^2 -(-6x)\cdot 4x(x^2-1)}{\left(x^2 -1\right)^4} =\]" title="Rendered by QuickLaTeX.com"/> \cfrac{-6 \left(x^2-1 \right)^2 + 24x^2(x^2-1)}{\left(x^2 -1\right)^4}” title=”Rendered by QuickLaTeX.com”> <p class=$ Tüm terimler var

$(x^2-1)$

dolayısıyla kesri basitleştirebiliriz:

$f''(x)= \cfrac{-6 \left(x^2-1 \right)^{\cancel{2}} + 24x^2\cancel{(x^2-1)}}{\left(x^2-1 \right)^\cancelto{3}{4}} =\cfrac{-6 \left(x^2-1 \right) + 24x^2}{\left(x^2 -1\right)^3}$

$f''(x)= \cfrac{-6x^2+6 + 24x^2}{\left(x^2 -1\right)^3} =\cfrac{18x^2+6}{\left(x^2 -1\right)^3}$

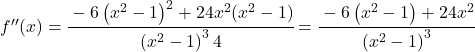
Şimdi ikinci türevi 0’a eşitliyoruz ve denklemi çözüyoruz:

$f''(x)= 0$

$\cfrac{18x^2+6}{\left(x^2 -1\right)^3}=0$

$18x^2+6=0\cdot \left(x^2 -1\right)^3$

$18x^2+6= 0$

$18x^2=-6$

$x^2=\cfrac{-6}{18}$

$x^2=-0,33$

$x=\sqrt{-0,33} \quad \color{red}\bm{\times}$

Negatif bir sayının karekökü yoktur. Yani eşleşen bir nokta yok

$f''(x)=0$

Şimdi bulunan tüm tekil noktaları, yani tanım kümesine ait olmayan noktaları (x=-1 ve x=+1) ve ikinci türevi iptal eden noktaları (bu durumda yoktur) doğru üzerinde temsil ediyoruz. herhangi):

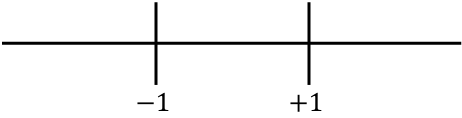
Ve fonksiyonun içbükey mi yoksa dışbükey mi olduğunu bilmek için her aralıkta ikinci türevin işaretini değerlendiririz. Bu nedenle her aralıkta bir nokta alıyoruz (asla tekil noktaları değil) ve bu noktada ikinci türevin hangi işarete sahip olduğuna bakıyoruz:

$f''(-2)=\cfrac{18(-2)^2+6}{\left((-2)^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

$f''(0)=\cfrac{18\cdot 0^2+6}{\left(0^2 -1\right)^3}= \cfrac{6}{-1} = -6 \ \rightarrow \ \bm{-}$

$f''(2)=\cfrac{18\cdot 2^2+6}{\left(2^2 -1\right)^3}= \cfrac{78}{27} = 2,89 \ \rightarrow \ \bm{+}$

İkinci türevin pozitif olması fonksiyonun dışbükey olduğu anlamına gelir.

$(\bm{\cup})$

ve ikinci türev negatifse bu, fonksiyonun içbükey olduğu anlamına gelir

$(\bm{\cap})$

. Bu nedenle içbükeylik ve dışbükeylik aralıkları şöyledir:

Dışbükey

$(\bm{\cup})$

$\bm{(-\infty, -1) \cup (1, +\infty)}$

İçbükey

$(\bm{\cap})$

$\bm{(-1,1)}$

Ancak x=-1 ve x=1 noktalarında eğrilikte değişiklik olmasına rağmen bunlar bükülme noktaları değildir. Çünkü işlev alanına ait değiller.

Ve son olarak, gerçekleştirilen tüm hesaplamaları kullanarak fonksiyonun grafiğini çiziyoruz:

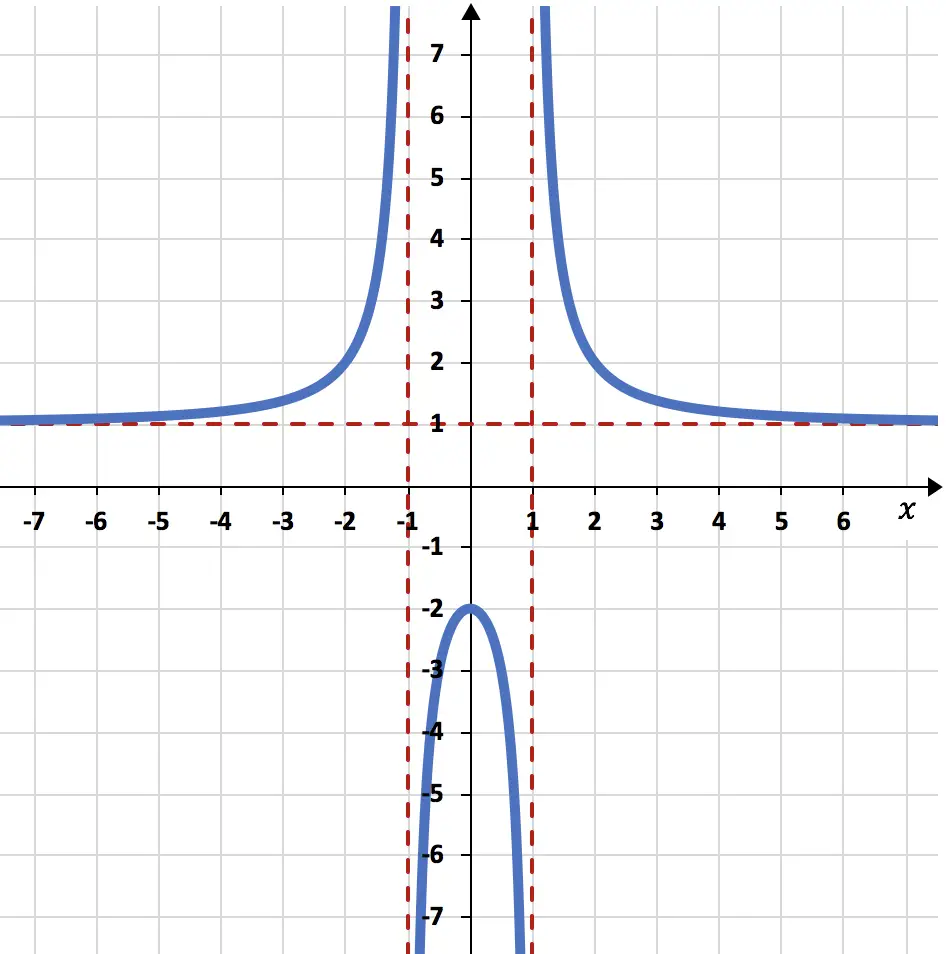
grafik fonksiyonları alıştırması çözüldü

Alıştırma 3

Aşağıdaki rasyonel fonksiyonu bir grafik üzerinde çizin:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Çözümü görün

Bu rasyonel bir fonksiyondur, dolayısıyla hangi sayıların fonksiyonun tanım kümesine ait olmadığını görmek için paydayı 0’a eşitlememiz gerekir:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

X ekseni ile kesişme noktasını bulmak için çözüyoruz

$f(x)= 0.$

Fonksiyonun X ekseninde değeri her zaman 0 olduğundan:

$f(x)=0$

$\cfrac{x^3}{x^2-4}=0$

$x^3=0\cdot (x^2-4)$

$x^3=0$

$x=\sqrt[3]{0}=0$

Dolayısıyla X ekseniyle kesişme noktası şu şekildedir:

$\bm{(0,0)}$

Y ekseniyle kesişme noktasını bulmak için şunu hesaplıyoruz:

$f(0).$

Y ekseninde x her zaman 0 olduğundan:

$f(0)=\cfrac{0^3}{0^2-4} = \cfrac{0}{-4} = 0$

Dolayısıyla Y ekseniyle kesişme noktası şu şekildedir:

$\bm{(0,0)}$

Bu durumda fonksiyon koordinatların orijininden geçtiği için X ekseniyle kesişme noktası Y ekseniyle kesişme noktasıyla çakışır.

Fonksiyonun düşey asimptotları olup olmadığını görmek için, fonksiyonun tanım kümesine ait olmayan noktalardaki limitini hesaplamamız gerekir (bu durumda x=-2 ve x=+2). Ve eğer sonuç sonsuzsa bu dikey bir asimptottur. Henüz:

$\displaystyle \lim_{x \to -2} \cfrac{x^3}{x^2-4} = \cfrac{(-2)^3}{(-2)^2-4} =\cfrac{-8}{4-4}= \cfrac{-8}{0} = \infty$

Fonksiyonun x -2’ye yaklaşırken limiti sonsuzluk verdiğinden, x=-2 dikey bir asimptottur.

Asimptot x=-2’nin yanal sınırlarını, ona çok yakın bir sayıyı fonksiyonda değiştirerek hesaplıyoruz:

$\displaystyle f(-2,1)=\cfrac{(-2,1)^3}{(-2,1)^2-4} =-22,59 \longrightarrow \lim_{x \to -2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(-1,9)=\cfrac{(-1,9)^3}{(-1,9)^2-4} =+17,59 \longrightarrow \lim_{x \to -2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

Şimdi x=+2’nin dikey bir asimptot olup olmadığına bakalım:

$\displaystyle \lim_{x \to +2} \cfrac{x^3}{x^2-4} = \cfrac{(2)^3}{(2)^2-4} =\cfrac{8}{4-4}= \cfrac{8}{0} = \infty$

Fonksiyonun x +2’ye yaklaşırken limiti sonsuzluk verdiğinden, x=+2 dikey bir asimptottur.

Asimptot x=2’nin yanal sınırlarını, ona çok yakın bir sayıyı fonksiyonda değiştirerek hesaplıyoruz:

$\displaystyle f(1,9)=\cfrac{1,9^3}{1,9^2-4} =-17,59 \longrightarrow \lim_{x \to 2^{-}} \cfrac{x^3}{x^2-4} = -\infty$

$\displaystyle f(2,1)=\cfrac{2,1^3}{2,1^2-4} =22,59 \longrightarrow \lim_{x \to 2^{+}} \cfrac{x^3}{x^2-4} = +\infty$

Öte yandan fonksiyonun yatay asimptotu fonksiyonun sonsuz limitinin sonucu olacaktır. Henüz:

$\displaystyle \lim_{x \to +\infty} \ \cfrac{x^3}{x^2-4} = \cfrac{+\infty}{+\infty } =+\infty$

Fonksiyonun sonsuz limiti bize +∞ değerini verdi, dolayısıyla fonksiyonun yatay asimptotu yok.

Şimdi eğik asimptotu hesaplıyoruz. Eğik asimptotlar şu şekildedir:

$y=mx+n.$

$m$

Aşağıdaki formülle hesaplanır:

$\displaystyle m = \lim_{x \to +\infty} f(x):x = \lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: x =\lim_{x \to +\infty} \cfrac{x^3}{x^2-4}: \frac{x}{1}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3\cdot 1}{(x^2-4)\cdot x} =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x}$

$\displaystyle m =\lim_{x \to +\infty}\cfrac{x^3}{x^3-4x} = \frac{+\infty}{+\infty} = \frac{1}{1} = \bm{1}$

Eğik asimptotun eğimini bildiğimizde, aşağıdaki formülü kullanarak kesişimi belirleriz:

$\displaystyle n = \lim_{x \to +\infty} \left[f(x)-mx\right] = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-1x\right]$

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-x\right] = \cfrac{+\infty}{+\infty} - (+\infty) = \bm{+\infty - \infty}$

Ancak ∞ – ∞ belirsizliğini elde ederiz. Bu nedenle terimleri ortak bir paydaya indirgemek gerekir. Bunu yapmak için x’i kesrin paydasıyla çarpıp bölüyoruz:

$\displaystyle n = \lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x \cdot (x^2-4)}{(x^2-4)}\right] =\lim_{x \to +\infty} \left[ \cfrac{x^3}{x^2-4}-\cfrac{x^3-4x}{x^2-4}\right]$

$\displaystyle n = \lim_{x \to +\infty} \cfrac{x^3- (x^3-4x)}{x^2-4} = \lim_{x \to +\infty} \cfrac{4x}{x^2-4}$

$\displaystyle n =\lim_{x \to +\infty} \cfrac{4x}{x^2-4} = \cfrac{+\infty}{\infty} =\bm{0}$

Kısaca eğik asimptot:

$y = mx+n$

$y = 1x + 0$

$\bm{y = x }$

Fonksiyonun monotonluğunu incelemek için önce türevini hesaplamalıyız:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

Şimdi türevi 0’a eşitliyoruz ve denklemi çözüyoruz:

$f'(x)= 0$

$\cfrac{x^4-12x^2}{\left(x^2-4\right)^2}=0$

$x^4-12x^2=0\cdot \left(x^2-4\right)^2$

$x^4-12x^2=0$

$x^2(x^2-12)=0$

$\displaystyle x^2\cdot(x^2-12) =0 \longrightarrow \begin{cases} x^2 =0 \ \longrightarrow \ \bm{x=0} \\[2ex] x^2-12=0 \ \longrightarrow \ x=\sqrt{12} \ \longrightarrow \ \bm{x= \pm 3,46} \end{cases}$

Şimdi bulunan tüm tekil noktaları, yani tanım kümesine ait olmayan noktaları (x=-2 ve x=+2) ve türevi iptal eden noktaları (x=0, x=-) doğru üzerinde temsil ediyoruz. 3,46 ve x= +3,46):

$f'(-4)= \cfrac{(-4)^4-12(-4)^2}{\left((-4)^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

$f'(-3)= \cfrac{(-3)^4-12(-3)^2}{\left((-3)^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(-1)= \cfrac{(-1)^4-12(-1)^2}{\left((-1)^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(1)= \cfrac{1^4-12\cdot1^2}{\left(1^2-4\right)^2} = \cfrac{-11}{9} = -1,22 \ \rightarrow \ \bm{-}$

$f'(3)= \cfrac{3^4-12\cdot 3^2}{\left(3^2-4\right)^2} = \cfrac{-27}{25} = -1,08 \ \rightarrow \ \bm{-}$

$f'(4)= \cfrac{4^4-12\cdot 4^2}{\left(4^2-4\right)^2} = \cfrac{64}{144} = 0,44 \ \rightarrow \ \bm{+}$

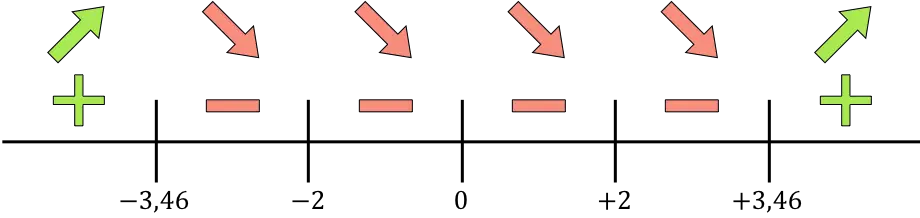
Türev pozitifse fonksiyon artıyor, türev negatifse fonksiyon azalıyor demektir. Buna göre büyüme ve düşüş aralıkları şöyledir:

Büyüme:

$\bm{(-\infty,-3,46)\cup (3,46,+\infty)}$

Azaltmak:

$\bm{(-3,46,-2)\cup(-2,0)\cup (0,2) \cup (2,3,46)}$

Fonksiyon x=-3,46’da artandan azalana doğru gider, dolayısıyla x=-3,46 fonksiyonun maksimumudur. Ve fonksiyon x=3,46’da azalan durumdan artana doğru gidiyor, yani x=3,46 fonksiyonun minimumudur.

Göreceli uçların Y koordinatlarını belirleriz:

$f(-3,46)=\cfrac{(-3,46)^3}{(-3,46)^2-4} = \cfrac{-41,42}{7,97}=-5,20 \ \longrightarrow \ (-3,46,-5,20)$

$f(3,46)=\cfrac{3,46^3}{3,46^2-4} = \cfrac{41,42}{7,97}=5,20 \ \longrightarrow \ (3,46,5,20)$

Dolayısıyla fonksiyonun göreceli ekstremleri şöyledir:

Maksimum nokta

$\bm{(-3,46,-5,20)}$

Minimum noktaya

$\bm{(3,46,5,20)}$

Fonksiyonun eğriliğini incelemek için fonksiyonun ikinci türevini hesaplıyoruz:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Şimdi ikinci türevi 0’a eşitliyoruz ve denklemi çözüyoruz:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

$x(8x^2+96)=0$

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Reel sayının negatif kökü olmadığı için çözüm de yoktur.

Şimdi bulunan tüm tekil noktaları, yani tanım kümesine ait olmayan noktaları (x=-2 ve x=+2) ve ikinci türevi iptal eden noktaları (x=0) doğru üzerinde temsil ediyoruz:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot 1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

İkinci türevin pozitif olması fonksiyonun dışbükey olduğu anlamına gelir.

$(\bm{\cup})$

ve ikinci türev negatifse bu, fonksiyonun içbükey olduğu anlamına gelir

$(\bm{\cap})$

. Bu nedenle içbükeylik ve dışbükeylik aralıkları şöyledir:

Dışbükey

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

İçbükey

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

Ancak x=-2 ve x=+2 noktalarında eğrilikte değişiklik olmasına rağmen bunlar bükülme noktaları değildir. Çünkü x=-2 ve x=+2 fonksiyonun tanım kümesine ait değildir. Öte yandan x=0 noktasında eğrilikte bir değişiklik olur (fonksiyon dışbükeyden içbükey hale gelir) ve bu fonksiyona aittir, dolayısıyla x=0 bir dönüm noktasıdır.

Büküm noktasının diğer koordinatını bulmak için bulunan büküm noktalarını orijinal fonksiyonda yerine koyarız:

$f(0) = \cfrac{0^3}{0^2-4} = \cfrac{0}{-4} =0\ \longrightarrow \ (0,0)$

Dolayısıyla fonksiyonun dönüm noktaları şunlardır:

Dönüş noktası:

$\bm{(0,0)}$

Son olarak hesapladığımız tüm bilgilere dayanarak fonksiyonu temsil ediyoruz:

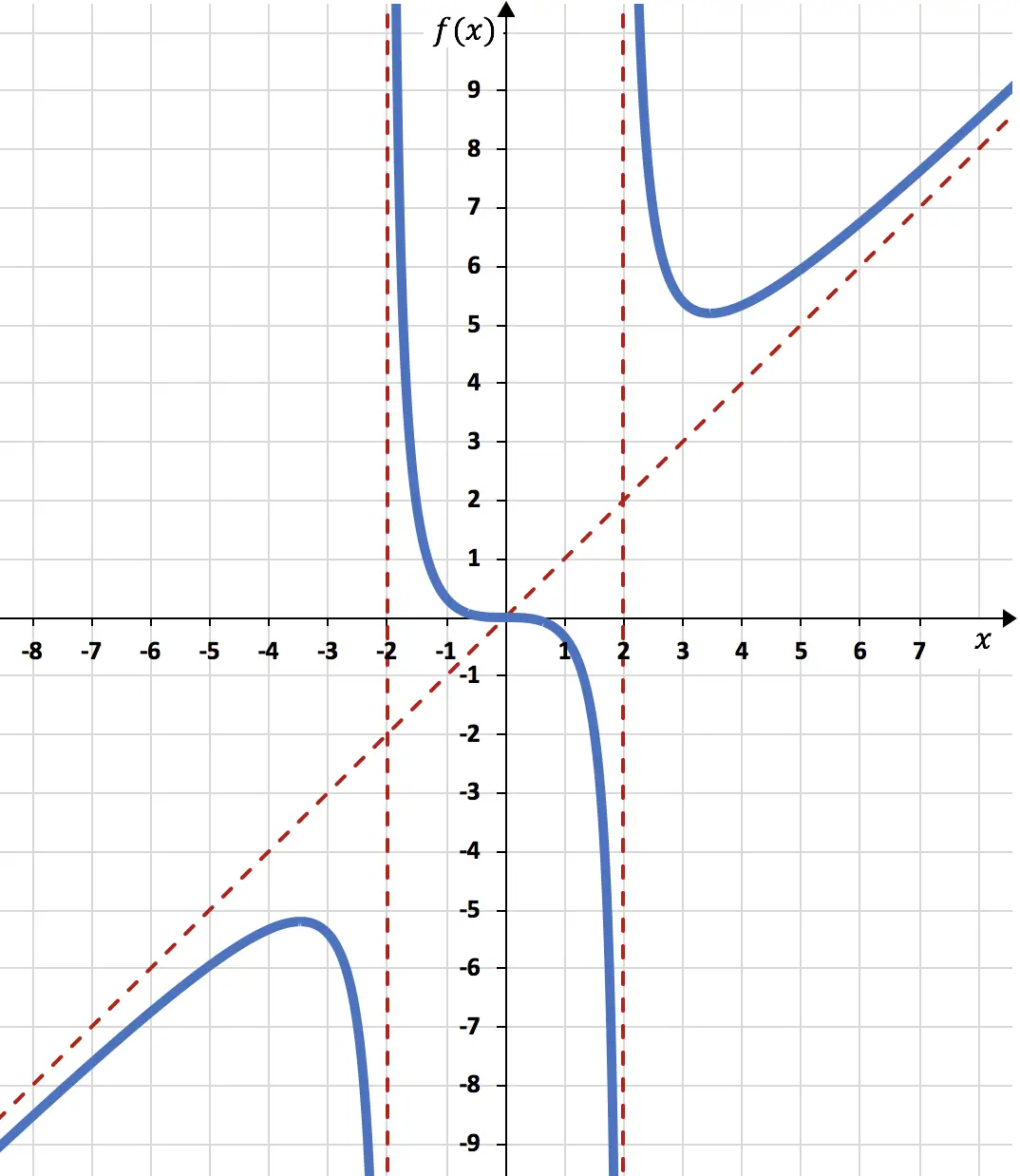
çözülmüş fonksiyonların grafik gösterimi, alıştırmalar

Yorum: Fonksiyonun eğik asimptotu bu noktada kestiğine dikkat edin.

$(0,0) .$

Gerçekten de, eğik asimptotlar her şeyden önce x +∞ ve -∞’a doğru yöneldiğinde fonksiyonun davranışını belirler; aslında fonksiyon hiçbir zaman grafiğin sağındaki (x→+∞) ve grafiğin solundaki eğik asimptotu geçmez. grafik (x→-∞). Ancak fonksiyonun ortadaki eğik asimptotu geçmesi çok nadirdir, çok özel bir durumdur.

Fonksiyon gösterimi

Bir fonksiyon grafikte nasıl temsil edilir?

Bir işlevi temsil etme örneği

Fonksiyonları temsil etmeye yönelik çözülmüş alıştırmalar

1. Egzersiz

Alıştırma 2

Alıştırma 3

Yorum bırakın Yanıtı iptal et