Polinom çarpanlarına ayırma nedir? Bir polinomu daha basit faktörlere veya ifadelere ayırmanıza olanak tanıyan matematiksel bir tekniktir. Ve bu sadeleştirme sayesinde birçok cebirsel ifade arasındaki işlemleri daha kolay ve rahat yapabileceğiz. Bu nedenle, bu makale boyunca polinomları çarpanlara ayırmanın farklı yöntemlerini ve tüm olası çarpanlara ayırma durumlarını tartışacağız.
Bir polinom nasıl çarpanlara ayrılır?
Kendi çözüm yapısına sahip olan ancak sonuçta aynı şeye dayanan birçok çarpanlara ayırma yöntemi vardır. Ek olarak polinom konfigürasyonuyla ilgili çok çeşitli durumları da bulabilirsiniz. Bu nedenle aşağıdaki bölümlerde mevcut tüm prosedürleri ve bunların her birinin ne zaman kullanılacağını tartışacağız. Son olarak kavramları öğrenmeyi tamamlamanız için bunu gerçek bir örneğe uygulayacağız.
Ruffini kuralıyla bir polinomu çarpanlarına ayırın
Polinomları çarpanlara ayırmak için en çok kullanılan yöntemRuffini kuralıdır çünkü kullanımı kolaydır ve sonuç hızlı bir şekilde bulunabilir. Normal olan, dereceleri ikiden büyük olan polinomları çarpanlara ayırmak, hatta bazen ikinci dereceden polinomları çarpanlara ayırmak için bu tekniği kullanmaktır. Bu polinomun köklerini çok grafiksel olarak almanızı sağladığı için. Ancak bu tür bir matematiksel ifadenin köklerine odaklanan bir sonraki bölümde bu kullanım açıklanacaktır.
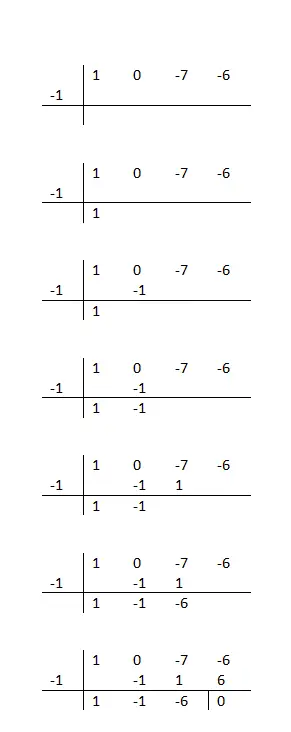
Polinomları çarpanlarına ayırmak için Ruffini nasıl yapılır?
Temel olarak, bölüşümün katsayılarını yatay bir çizgiye ve polinomun olası kökünün değerini de yan tarafa yazmamız gerekecek. Mümkün diyoruz çünkü sıfıra eşit bir kalan elde etmemizi sağlayacak bir bölen aramamız gerekecek. Aksi takdirde bu sayı geçerli bir kök olmayacak ve denemeye devam etmeniz gerekecektir.
İpucu olarak, yalnızca bağımsız terimin bölen sayılarını (yatay çizginin son değeri) denemenizi öneririz. Dolayısıyla seçtiğiniz sayının doğru olup olmadığını öğrenmek için aşağıdaki hesaplama sırasını izlemeniz yeterlidir:
Katsayıyı azaltıyorsunuz, test ettiğiniz kökle çarpıyorsunuz, bir sonraki katsayının altına yazıyorsunuz ve dikey toplama yapıyorsunuz. Bu adımları sonuna kadar tekrarlamanız gerekecek ve işiniz bittiğinde bu değerin doğru olup olmadığını bileceksiniz. Çünkü yalnızca sıfır kalanını veren sayılar geçerli olacaktır.
İzlemeniz gereken matematiksel prosedür size çok açık gelmediyse bu metnin solundaki sütundaki örneğe bakabilirsiniz. Ayrıca şu polinomu çarpanlara ayırmaya çalışmanızı öneririz: x³ + 2x² – x – 2 (örneğe göre). Son olarak, alıştırmayı doğru çözüp çözmediğinizi öğrenmek için sonucunuzu şununla karşılaştırabilirsiniz:
- Aşırı ifade = x² + 3x + 2
- kalan = 0
Şimdi Ruffini’nin çarpanlara ayırmada uygulanmasına dair kısa bir açıklama yapacağız. Ancak bu matematiksel kaynağın nasıl kullanıldığını ayrıntılı olarak öğrenmek istiyorsanız, bağlantı verdiğimiz son makaleye erişmenizi öneririz, çünkü burada her şey çok iyi anlatılmıştır. Bununla birlikte, polinomların Ruffini kuralıyla nasıl çarpanlara ayrılacağını açıklayarak başlayalım:
- Izgarayı çiziyoruz: Yukarıdaki görselde de gördüğümüz gibi Ruffini yapacağımız bir kutu oluşturacağız. Temel olarak ifadenin katsayılarını yatay olarak ve sıfır değeri olanları bırakmadan yazmanız gerekir. Sonuçta resimdekine benzer ancak polinomunuzun değerlerine sahip bir temsile sahip olmalısınız.
- Kökleri hesaplıyoruz: Yapıyı çizdikten ve tüm sayıların doğru yazıldığından emin olduktan sonra kökü hesaplamaya geçeceğiz. Bu listenin hemen üstünde (resimli) bahsettiğimiz hesaplama sırasını takip ederek kökleri bulmanız gerekecek.
- Kökü (x – a) biçiminde ifade ederiz: polinomun tüm köklerine sahip olduğumuzda, bunları aşağıdaki (x – a) biçiminde ifade etmemiz gerekir. A’nın elde ettiğimiz değerler olduğunu dikkate alırsak, örneğin sonuç x = 2, x = -2 ve x = 4 olarak çıkarırsak, (x – 2), (x + 2) ve (‘yi elde ederiz. x – 4).
- Tüm faktörleri tek bir ifadede topluyoruz: Son olarak, tüm kökleri zaten doğru formatta ifade ettiğimizde, onları tek bir cebirsel ifadede toplamamız gerekecek. Önceki örnekten devam edersek şöyle bir şey elde ederiz: (x – 2) · (x + 2) · (x – 4).
Bir polinomun köklerini kullanarak bir polinomu çarpanlarına ayırın
Bir polinomun kök kavramını Ruffini’nin bölümünde yarım açıklamıştık. Ancak tam tanım şu şekilde olacaktır: Bir P(x) polinomunun kökü , P(a) = 0 olacak şekilde sayısal bir a değeridir. Bu nedenle söz konusu fonksiyonu veya polinomu iptal edebilen bir sayıdır. Özetle, bir polinomu faktörlerin çarpımına ayrıştırmak için kullanıldığını söyleyebiliriz.
Örneğin, bize aşağıdaki x² − x − 2 ifadesi verilirse ve bunu Ruffini kuralını kullanarak ya da basitçe ikinci dereceden x² − x − 2 = 0 denklemini çözerek çarpanlara ayırırsak. İki x değeri = -1 elde ederiz ve x = 2, yani bunları (x – a) biçimine çevirip bir araya getirirsek, şu ifadeye ulaşırız: (x + 1) (x − 2), yani çarpanlara ayrılmış polinom . İfade birden fazla terimden oluşmasına rağmen bunu derecesi ikiden büyük polinomlara uygulayabiliriz.
Bir polinomun ortak faktör çıkarımı yoluyla çarpanlara ayrılması
Bağımsız terimi olmayan polinomları veya tüm terimlerde ortak çarpanı olan ifadeleri çarpanlara ayırmak istediğimizde bu tekniği kullanarak polinomu basitleştirebiliriz. Temel olarak , dağılım özelliğinin ifadenin tamamına uygulanmasını , tekrar eden ortak faktörün çıkarılmasını ve tüm polinomun çarpılmasıyla eklenmesini içerir. Aşağıda bahsettiğimiz ilk durumun bir örneğini bulacaksınız (bağımsız terimi olmayan polinom):
2x³ + 10x² – 6x = 2x (x² + 5x – 3)
Ortak faktörün çift ekstraksiyonu
Ortak faktör çıkarımı, birden fazla değişken içeren daha karmaşık faktörlerin çıkarılmasıyla bile yapılabilir. Hatta ana ifadenin kendisinden türetilen polinomları bile çıkarabilirsiniz. Bu tür bir işlemi gerçekleştirmek istediğinizde sınır koymamak önemlidir, çünkü faktör çıkarmanın amacı cebirsel bir ifadeyi mümkün olduğu kadar basitleştirmektir .
Önemli kimlikleri kullanarak polinomları çarpanlara ayırma
Dikkate değer ürünler, bir tür basitleştirilmiş cebirsel ifadeler oldukları için polinom ifadelerini çarpanlarına ayırmamıza yardımcı olabilir. Bu nedenle uzun bir polinomdan doğrudan birkaç terimden oluşan küçük bir formüle geçmemize yardımcı olurlar. Bu nedenle, bunları ne zaman kullanabileceğinizi hızlı bir şekilde tanımlayabilmek için dikkate değer kimlik formüllerini öğrenmeniz önemle tavsiye edilir. Bu da Ruffini veya diğer yöntemlerden herhangi birini kullanarak çarpanlara ayırma konusunda bize zaman kazandırıyor. Daha sonra öğrenmeniz gereken üç kuralı ele alacağız:
- Kareler farkı: a² – b² = (a + b) · (a – b)
- Toplamın karesi: a² + 2ab + b² = (a + b)²
- Çıkarma karesi: a² – 2ab + b² = (a – b)²
Polinomları gruplandırarak çarpanlara ayırma
Bazı durumlarda , x² – ax – bx + ab yapısında bir polinom bulabiliriz; bu polinom, ortak bir faktörün çıkarılmasıyla basitleştirilebilir: x (x – a) – b (x – a). Ve ortak çarpanı tekrar alırsak, daha da basitleştirilebilir: (x – a) · (x – b). Dolayısıyla bu polinomun kökleri x = a ve x = b olacaktır. Gördüğünüz gibi bu tür cebirsel ifadeler çarpanlara ayrılması ve kullanımı oldukça kolay bir yapıya sahiptir.
Polinom çarpanlara ayırma alıştırmaları
Son olarak polinomları çarpanlara ayırma alıştırması yapabilmeniz için size bir dizi alıştırma sunmak istiyoruz. Bu sayede bugün anlattığımız teoriyi daha iyi içselleştirebileceksiniz. Basitçe, defterinizdeki alıştırmaları çözmeli ve sonuçları aşağıda size sunduğumuz sonuçlarla karşılaştırmalısınız.
- x 4 -1 = (x 2 + 1) (x + 1) (x – 1)
- x 5 + x 4 – x – 1 = (x – 1) (x + 1) 2 (x 2 + 1)
- 9×2 + 30x + 25 = (3x + 5) 2
- x 4 – 3x 3 – 3x 2 + 11x – 6 = (x + 2) (x – 3) (x – 1) 2