Evrimsel matris - Mathority

Bu sayfada içe dönen matrisin ne olduğunu öğreneceksiniz. Ayrıca size 2×2, 3×3 ve 4×4 boyutlarındaki dahil edici matris örneklerini de gösteriyoruz. Ve son olarak evrimsel matrisin formülünü bulacaksınız.

Evrimsel matris nedir?

Evrimsel matrisin anlamı aşağıdaki gibidir:

İnvolütif matrisin tanımı : Ters matrisi matrisin kendisi olan tersinir bir kare matris.

$A^{-1} = A$

Altın

$A$

herhangi bir matristir ve

$A^{-1}$

tersini temsil eder.

Açıkçası bir evrimsel matris , düzenli veya dejenere olmayan bir matrisin bir örneğidir .

Bir matrisin tersinin ne olduğunu bilmiyorsanız, burada 3×3 ters matrisin nasıl hesaplanacağını görebilirsiniz. Bir matrisin nasıl ters çevrileceğini bilmek önemlidir, ancak bunun için bir matrisin ekinin nasıl hesaplandığını da bilmeniz gerekir.

Ancak konuya dönelim: Bir matris kapsayıcı olduğunda, matrisin matrisin kendisi ile çarpılması birim matrisi verir. Demoya bir göz atın:

Herhangi bir matrisin tersiyle çarpılması Kimlik (veya Birim) matrisini verir. BU YÜZDEN:

$\displaystyle A \cdot A^{-1} = I$

Ve bir evrimsel matrisin tersi matrisin kendisi olduğundan:

$\displaystyle A \cdot A = I$

Sonuç olarak, kareli bir evrimsel matris birim matrisi verir:

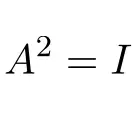
Evrimsel matris örnekleri

2 × 2’lik bir içe giren matris örneği:

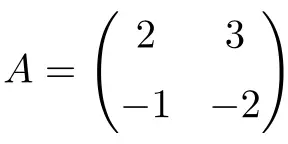
Matrisin ikinci gücünü hesaplayarak bunun bir evrimsel matris olduğunu doğrulayabiliriz:

$\displaystyle A^2=\begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix} \cdot \begin{pmatrix} 2 & 3 \\[1.1ex] -1 & -2 \end{pmatrix}= \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix}$

A kare matrisi birim matris olduğundan, A matrisi 2×2 evrilmiş bir matristir.

3 × 3’lük bir içe giren matris örneği:

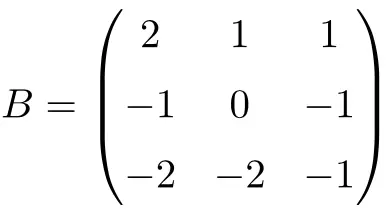
Matrisin çarpımını tek başına çözerek bunun bir evrimsel matris olduğunu doğrulayabiliriz:

$\displaystyle B^2=\begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}\cdot \begin{pmatrix} 2 & 1 & 1 \\[1.1ex] -1 & 0 & -1 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

B kare matrisi birim matris olduğundan, B matrisi 3×3 evrilmiş bir matristir.

4×4 içe dönen matris örneği:

Kimlik (veya Birim) matrisi, boyutu ne olursa olsun, tanımı gereği bir evrimsel matristir.

$\displaystyle I=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Matrisin değerini 2’ye yükselterek bunun bir evrimsel matris olduğunu doğrulayabiliriz:

$\displaystyle I^2=\begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}\cdot \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}= \begin{pmatrix} 1 & 0 & 0 & 0 \\[1.1ex]0 & 1 & 0 & 0\\[1.1ex]0 & 0 & 1 & 0 \\[1.1ex]0 & 0 & 0 & 1 \end{pmatrix}$

Karesi birim matris birim matrisi olduğundan birim matrisi 4×4 evrilme matrisidir.

Açıkçası birim matris herhangi bir boyutta olabilir, çünkü bu sadece ana köşegeninde tüm 1’ler ve geri kalanı 0 olan bir köşegen matristir. Dolayısıyla birim matrisi, sırası ne olursa olsun her zaman bir evrimsel matris olacaktır.

İçeren matris formülü

Evrimsel matrisin özelliklerinden biri de formülünün bilinebilmesidir. Ancak ikinci dereceden evrimsel matris formülünün ispatı oldukça sıkıcı olduğundan sizi doğrudan sonuca bırakacağız, asıl önemli olan da bu. Demoyu daha çok ilginizi çekiyorsa aşağıda yorumlarda adım adım anlatıldığını görebilirsiniz.

2 × 2 boyutlu bir kapsayıcı matrisin formülü aşağıdaki gibidir:

Bu nedenle, ana köşegen değerleri zıt olan ve determinantı -1 olan herhangi bir matris, bir involüsyonel matris olacaktır.

Bununla birlikte, bu formülle tanımlanan matrislere ek olarak birim matris ve onun tersinin de 2. mertebeden evrimsel matrisler olduğu dikkate alınmalıdır:

$\displaystyle \begin{pmatrix} 1 & 0 \\[1.1ex] 0 & 1 \end{pmatrix} \qquad \begin{pmatrix} -1 & 0 \\[1.1ex] 0 & -1 \end{pmatrix}$

İçeren bir matrisin özellikleri

Evrimsel matrisler aşağıdaki özelliklere sahiptir:

Bir evrimsel matrisin determinantı her zaman -1 veya +1’e eşittir.

Evrimsel matrisler ile idempotent matrisler arasında bir ilişki vardır : matris
$A$

ancak ve ancak matrisin evrimsel olması

$\displaystyle Q= \cfrac{1}{2} \cdot (A+I)$

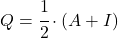
idempotenttir.

Evet
$A$

Ve

$B$

iki değişmeli evrimsel matris varsa, o zaman matris çarpımı

$AB$

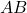
aynı zamanda başka bir evrimsel matristir.

Bir evrimsel matrisin herhangi bir kuvveti, başka bir evrimsel matrisle sonuçlanır. Özellikle, tek üs değerine yükseltilen bir evrimsel matris kendisine eşit olacaktır, diğer taraftan çift üs düzeyine yükseltildiğinde ise Özdeşlik matrisine eşdeğer olacaktır.

$A^2 = I$

$A^3 = A$