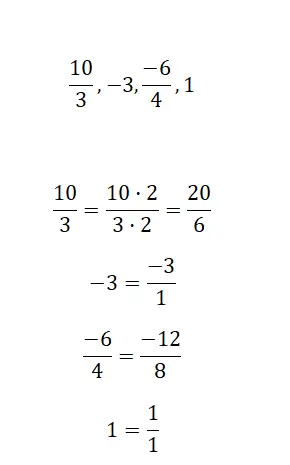Bu yazıda eşdeğer kesirler veya eşit kesirler hakkında çok eksiksiz ve anlaşılması kolay bir açıklama bulacaksınız. Daha spesifik olarak bunların tanımlarından, nasıl hesaplanacağından ve iki kesrin eşdeğer olup olmadığının nasıl bilineceğinden bahsedeceğiz. Bu şekilde, sonunda size sunacağımız gibi eşdeğer kesirler ile ilgili alıştırmaları çözmek için ihtiyacınız olan her şeyi bileceksiniz. Bununla birlikte, konuyla başlayalım dedik.
Eşdeğer Kesirler Hesaplayıcı
Bu eşdeğer kesirler hesaplayıcının yardımıyla, herhangi bir hesaplama yapmanıza gerek kalmadan iki kesrin eşit olup olmadığını kontrol edebileceksiniz. İşlemi oldukça basittir, temel olarak iki pay ve iki paydaya karşılık gelen değerleri girmeniz ve “Hesapla” butonuna basmanız gerekir.
Eşdeğer kesirler nelerdir?
Eşdeğer kesirler , aynı sayısal değeri ifade eden , dolayısıyla pay ve paydaları farklı olsa bile aynı sonucu veren kesirlerdir. Bu, iki türden olabilen orantılı bir ilişkiye sahip oldukları anlamına gelir: güçlendirilmiş veya basitleştirilmiş. Daha sonra, kavramın daha iyi anlaşılması için size eşdeğer kesirlerin grafik bir örneğini göstereceğiz.
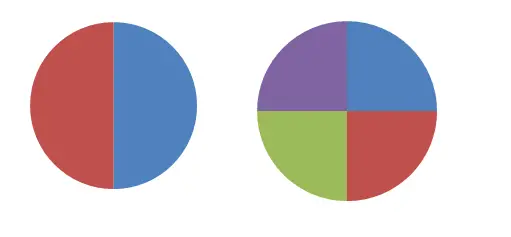
Önceki resimde iki ve dört parçaya bölünmüş iki daireyi görebilirsiniz. İlkini kesirle tanımlamaya çalışırsak her parçanın bütünün 1/2’sine eşit olduğunu söyleyeceğiz, ikinci şekilde ise 1/4 kesirini kullanacağız. Açıkçası, bu iki kesir farklı miktarları temsil ettikleri için eşdeğer değildir . Ancak ikinci dairenin iki parçasını (2/4) alırsak bu ifade 1/2’ye eşdeğerdir.
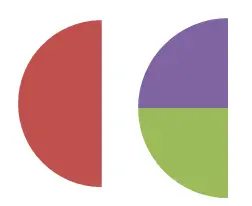
Bu ikinci görselde 1/2 ile 2/4 arasındaki denkliği görmekte ve sayısal olarak da doğrulayabilmektedir. 1/2 = 0,5 ve 2/4 = 0,5 olduğundan. Daha önce yorumladığımız tanıma göre eğer iki kesir aynı sayısal değeri ifade ediyorsa eşdeğer kesirdir.
Eşdeğer kesir örnekleri
Şimdi size eşdeğer kesirlerin 5 örneğini göstereceğiz. Bunları nasıl hesapladığımızı anlamak istiyorsanız okumaya devam etmenizi öneririz.
- Yarıma eşdeğer kesirler: 2/4, 3/6, 4/8 vb.
- Üçte bire eşdeğer kesirler: 2/6, 3/9, 4/12, vb.
- Çeyreğe eşdeğer kesirler: 2/8, 3/12, 4/16, vb.
- Birliğe eşit kesirler: 4/4, 7/7, 15/15, vb.
- Beşte bire eşdeğer kesirler: 2/10, 3/15, 4/20, vb.
Eşdeğer kesirler nasıl hesaplanır?
Eşdeğer kesirler elde etmek için pay ve paydayı aynı sayıyla çarpmamız veya bölmemiz gerekir. Çünkü kesrin her iki kısmını da aynı şekilde değiştirirsek orantılı bir ilişki sağlarız. Bu nedenle iki yöntem kullanabiliriz: amplifikasyon ve redüksiyon.
Amplifikasyonla eşdeğer bir kesir bulma
Bu ilk durumda, başlangıç kesirini belirli bir sayısal değerle çarpmamız gerekir. Bu, pay ve paydayı bu sayıyla çarpmamız gerektiği anlamına gelir. Bir örnekle görebilmeniz için, çarpma işlemi sonrasında elde edilen iki eşdeğer kesri aşağıda gösteriyoruz:
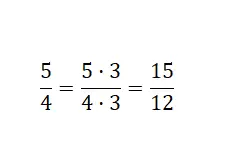
Yaptığımız kesrin her iki kısmını da üçle çarpmaktı: 5 x 3 = 15 ve 4 x 3 = 12 . Böylece daha büyük olduğu için yükseltilmiş eşdeğer bir kesir elde ederiz. Sonuç olarak, orijinal kesirle aynı miktarı ifade eden, farklı sayısal değerlerden oluşan bir kesir bulduk.
Sadeleştirme yoluyla eşdeğer bir kesir bulma
İkinci olarak, belirli bir kesrin payını ve paydasını bölerekbir kesri basitleştirmeyi seçebiliriz. Bu şekilde, birincisinden daha basit olan başka bir eşdeğer kesir elde edeceğiz. Bununla birlikte, bu yöntemin yalnızca ilk ifadenin indirgenemez bir kesir olmaması durumunda işe yaradığını belirtmekte fayda var, çünkü ikincisi daha fazla indirgenemez. Aşağıda indirgeme (sadeleştirme) yoluyla eşdeğer bir kesirin hesaplanmasına bir örnek verilmiştir.
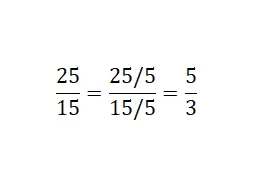
Resimde gördüğünüz gibi kesrin hem payını hem de paydasını ortak bir bölene böldük. Bu örnekte beş kullandık: 25/5 = 5 ve 15/5 = 3. Son olarak indirgenemez eşdeğer kesir olan 25/15’i elde ettik.
İki kesrin eşdeğer olup olmadığını nasıl anlarsınız?
Eşdeğer kesirleri belirlemek için aşağıda açıklayacağımız üç prosedürden birini izlemeliyiz. İkincisinin bir önceki bölümde bahsettiğimiz kesirlerin sadeleştirilmesiyle ilgili olduğunu belirtelim.
Payları paydalarla çarpmak
İki kesir arasındaki denkliği kontrol etmek istiyorsanız bu ilk prosedürü kullanabilirsiniz. Temel olarak, ilk kesrin payını ikincinin paydasıyla çarpmanız gerekir. Daha sonra, ikinci kesrin payını birincinin paydasıyla çarpmanız gerekir. Her iki sonuç da aynı sonucu verirse , bu kesirler eşdeğer olacaktır. Aşağıdaki örneğe bakın:
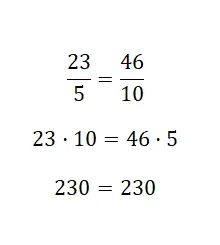
Bu son örnekte iki kesrin eşdeğer olduğunu doğruladık. Bu örneği görmek kolaydı, çünkü ikinci kesir birincinin iki katıdır, yani bunlar güçlendirilmiş bir denklik ilişkisine sahiptir. Bu prosedürün kullanımının oldukça rahat olduğunu, sadece haçları çarpmanın yeterli olduğunu belirtmekte fayda var. Ancak diğer iki sistemi nasıl kullanacağınızı da öğrenmenizi öneririz, çünkü bu size daha fazla matematiksel kaynak sağlayacaktır.
Kesirleri basitleştirin
İndirgenemeyen kesirler söz konusu olduğunda, en büyük sayılardan oluşan kesirin mümkün olduğu kadar azaltılmasını içeren bu diğer yöntemi kullanabiliriz. Bu indirgemeyi yaparken küçük kesrin diğerinin indirgenemez olduğunu bulursak, bunların eşdeğer olduğunu varsayabiliriz.
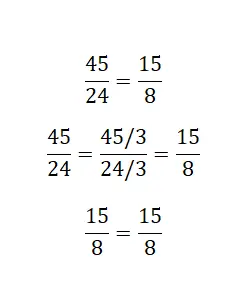
Bölmeleri çöz ve eşitle
Son olarak kesirlerle oluşturulan bölüm çözümüne başvurabilirsiniz çünkü karışık bir sayı her zaman bir bölmedir. Temel olarak, iki kesrin eşdeğer sayısal değerini hesaplamanız gerekir ve eğer aynı sayı ise, o zaman eşdeğer olacaktır. Aşağıdaki görselde çok net bir örnek görebilirsiniz:
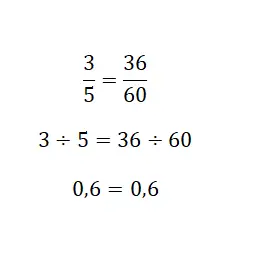
Eşdeğer kesirler üzerine alıştırmalar
Artık teorinin tamamını okuduğunuza göre, açıklamayı anlamayı tamamlamanıza olanak sağlayacak aşağıdaki alıştırmaları çözmeye çalışabilirsiniz. Bunları kendi başınıza çözmeye çalışmanızı ve çözdükten sonra sonucunuzu size sunduğumuz sonuçla karşılaştırmanızı öneririz. Bununla birlikte, pratik yapmanıza izin veriyoruz:
1. Egzersiz
Sunduğumuz her kesir için sadeleştirme yaparak eşdeğer bir kesir bulun:
Bu alıştırmayı çözmek için kesirlerin sadeleştirilmesini uygulayın, böylece eşdeğer indirgenemez kesri elde edin. Dört örnek birbirine çok benziyor, bu yüzden çözmede fazla zorluk yok.
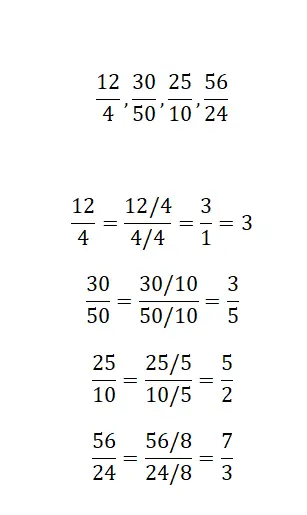
Alıştırma 2
Önerdiğimiz her kesir için büyütme yoluyla eşdeğer bir kesir bulun:
Daha sonra önerdiğimiz kesirleri büyütmeniz gerekecek, bu şekilde daha büyük eşdeğer kesirler elde edeceksiniz. Çarpma işlemini hangi sayıyla yaptığınızın bir önemi yok, örneğin 2 ve 3 ile yapacağız.
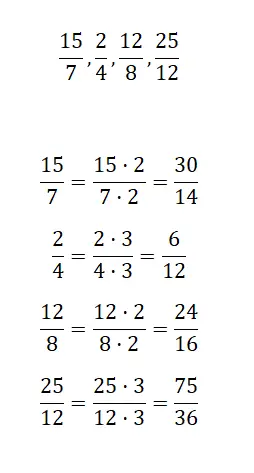
Alıştırma 3
Aşağıdaki kesirlerin eşdeğer olup olmadığını belirleyin:
İki kesrin eşdeğer olup olmadığını öğrenmek için yukarıda anlattığımız üç yöntemden birini kullanmanız gerekir. İstediğiniz sistemi kullanmakta özgür olmanıza rağmen, ilk prosedürde çözülen düzeltmeleri bulacaksınız.
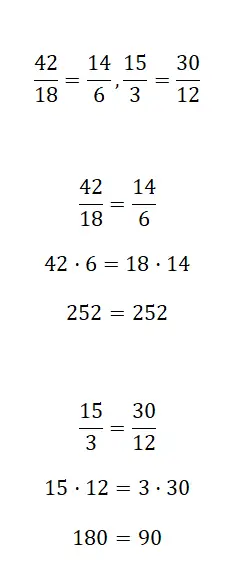
Alıştırma 4
Aşağıdaki ifadelerin eşdeğer kesirlerini hesaplayın:
Bu son alıştırmada, bir denklik ilişkisini korumaya çalışarak önerdiğimiz ifadeleri ( tam sayılar ve karışık sayılar) kesir biçiminde yeniden yazmanız gerekecek.