Bu sayfada iki doğrunun aynı düzlemde olmasının ne anlama geldiğini öğreneceksiniz. Ayrıca iki doğrunun eş düzlemli olduğunu görebileceksiniz ve buna ek olarak eş düzlemli doğrularla ilgili örnekler ve çözülmüş alıştırmalar bulacaksınız.
İki eş düzlemli çizgi nedir?
Analitik geometride eş düzlemli çizgilerin tanımı aşağıdaki gibidir:
İki doğru aynı düzlemde olduğunda eş düzlemlidir. Bu nedenle eş düzlemli çizgiler yalnızca kesen çizgiler , paralel çizgiler veya çakışan çizgiler olabilir.
Ayrıca, bir düzlemi tamamen tanımlamak için iki eş düzlemli çizgi yeterlidir. Her ne kadar bir düzlemin ikiden fazla ortak düzlemli çizgisi olabileceği açık olsa da, gerçekte her düzlem sonsuz sayıda çizgi içerir.
Öte yandan, eğer iki doğru aynı düzlemde değilse bu onların kesiştiği anlamına gelir.
Eş düzlemli çizgi örnekleri
Eş düzlemli çizgi kavramını daha iyi anlamanız için işte üç çizgiden oluşan bir örnek:
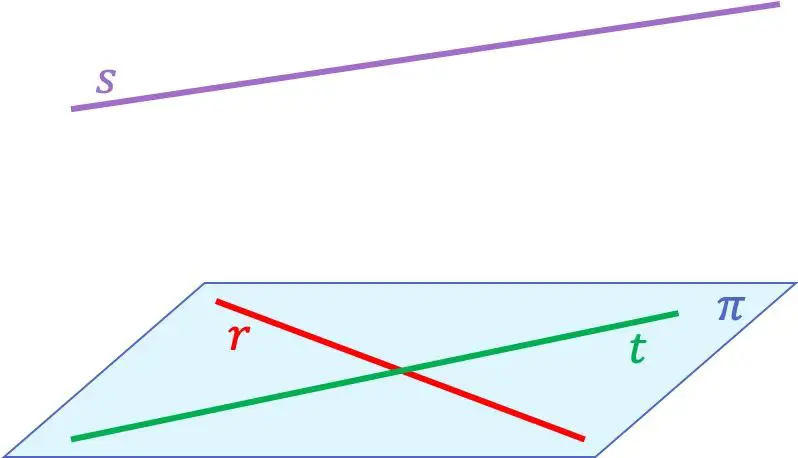
Bu durumda çizgiler
![]()
Ve
![]()
Aynı düzleme ait oldukları için eş düzlemlidirler. Bunun yerine düz çizgi
![]()
doğrularla kesiştiği için diğer iki doğruyla aynı düzlemde değildir
![]()
Ve
![]()
İki çizginin aynı düzlemde olup olmadığını nasıl anlarsınız?
Yukarıda eş düzlemli doğruların açıklamasında gördüğümüz gibi bunlar ancak kesen, paralel veya çakışan doğrular olabilir. Başka bir deyişle, 2 çapraz çizgi hiçbir zaman aynı düzlemde olmayacaktır.
Bu nedenle, iki doğrunun eş düzlemli olup olmadığını bilmek için aralarındaki göreceli konumun belirlenmesi gerekir; eğer bunlar kesişen, paralel veya çakışan iki çizgi ise, bu onların eş düzlemli olduğu anlamına gelir.
Bu nedenle, iki çizginin eş düzlemliliğini kontrol etmek için öncelikle iki çizginin uzaydaki göreceli konumunun nasıl hesaplanacağını bilmeniz gerekir. Eğer hala bu kavrama aşina değilseniz, ilk önce tam açıklamanın yanı sıra örnekler, alıştırmalar ve çözülmüş problemler bulabileceğiniz bağlantıya bakmanız en iyisidir.
Eş düzlemli çizgilerin çözülmüş egzersizi
Örnek olarak eş düzlemli çizgilerle ilgili tipik bir alıştırmayı çözeceğiz:
- Aşağıdaki iki çizginin aynı düzlemde olup olmadığını belirleyin:
![Rendered by QuickLaTeX.com \displaystyle r: \ \begin{cases} x=3-2t \\[1.7ex] y=4t \\[1.7ex] z=5 \end{cases} \qquad \qquad s : \ \begin{cases} 2x+y=0 \\[1.7ex] z=-2\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-76e57f7dd2bfa67f2cf4eb2ee0455dcf_l3.png)
Yapmamız gereken ilk şey, iki doğru arasındaki göreceli konumu bulmaktır ve bunun için her ikisini de aynı tür denklemle ifade etmiş olmalıyız. Sonra düz çizgiyi geçeceğiz
![]()
genel (veya örtülü) denklemden parametrik denklemlere:
![Rendered by QuickLaTeX.com \displaystyle s : \ \begin{cases} 2x+y=0 \\[1.7ex] z=-2\end{cases} \xrightarrow{x \ = \ t} \ \begin{cases} 2t+y=0 \\[1.7ex] z=-2\end{cases} \longrightarrow \ \begin{cases} x=t \\[1.7ex] y=-2t \\[1.7ex] z=-2\end{cases}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d8dbc805cb7e0020c9c82c90e56e011_l3.png)
Yani her çizginin yön vektörü:
![]()
İki doğrunun yön vektörlerinin koordinatları orantılı olduğundan sadece çakışık veya paralel doğrular olabilirler. Bu nedenle, bu özel durumda, paralel çizgiler ve çakışan çizgiler eş düzlemli doğrular olduğundan, göreceli konumun tam olarak hesaplanmasına gerek yoktur. Yani iki doğru aynı düzlemdedir .