En küçük ortak katı (lcm) hesaplayın

İki veya daha fazla sayının en küçük ortak katı (LCM), bu sayıların ortak olduğu en küçük (sıfır olmayan) kattır. Benzer yöntemler kullanılarak hesaplanmasına rağmen en büyük ortak bölenin ters işlemidir. LCM’nin nasıl hesaplanacağını öğrenmek istiyorsanız okumaya devam etmenizi öneririz çünkü bu makalede bir sayı kümesinin en küçük ortak katını bulmak için tüm prosedürleri (en basitinden en karmaşıkına kadar) açıklayacağız.

lcm hesaplayıcı

LCM’nin nasıl elde edileceği hakkında konuşmaya başlamadan önce, bu sayfada en az ortak çoklu hesaplayıcımızın olduğunu bilmenizi isteriz. Bununla istediğiniz tüm sayıların lcm’sini hesaplayabileceksiniz, bu şekilde egzersizlerinizin sonuçlarını karşılaştırarak bunları doğru çözüp çözmediğinizi görebilirsiniz.

Daha az yaygın olan çoklu hesap makinesini kullanmak için tam sayıları virgülle ayırarak girin:

lcm'yi hesapla

En küçük ortak kat nasıl hesaplanır?

İki veya daha fazla sayının en küçük ortak katını bulmak için aşağıda anlatacağımız üç yöntemden birini uygulamanız gerekir. Daha sonra seçebileceğiniz prosedürlerin her birini detaylandırdığımızda, bunların avantaj ve dezavantajlarının neler olduğunu da anlatacağız. Bu şekilde, söz konusu LCM'yi kolay ve hızlı bir şekilde çözmek için her durumda hangisini seçeceğinizi bileceksiniz.

Yöntem 1: Çoklu Liste

İlk yöntem, LCM'de hesaplamak istediğiniz sayıların katlarından oluşan bir liste oluşturmaktır. Daha sonra tüm listelerde tekrar eden en küçük değeri bulmanız gerekir, böylece en küçük ortak kata sahip olursunuz. Daha sonra bir örnekle göreceğiz: lcm (5, 6).

Yöntem 2: faktöriyel ayrıştırma

İkinci olarak sayıları çarpanlarına ayırmayı seçebiliriz. Daha spesifik olarak, bu yöntem büyük sayıların pcm'sini hesaplamayı kolaylaştıracaktır. Büyük sayıların 1cm'sini gerçekleştirirken yöntem 1'i takip etmek yavaş ve sıkıcı olabilir, çünkü çok uzun katlar listesi yazmamız gerekecek. Bu ikinci prosedürün anlaşılması ilk başta biraz daha karmaşık olabilir, ancak mekaniğini anladığınızda öncekine göre birçok avantajı vardır. Bununla birlikte, izlenecek prosedüre bakalım:

• Faktöriyel ayrıştırma: İlk adım, LCM'ye dahil edeceğimiz tüm sayıları asal faktörlere ayırmak olacaktır. Bir sayıyı faktöriyel olarak nasıl ayrıştıracağınızı bilmiyorsanız, bu son bağlantıya girmenizi öneririz; burada sayıları hızlı ve verimli bir şekilde nasıl basitleştireceğinize dair birinci sınıf bir açıklama bulacaksınız.
• Tek bir matematiksel ifade oluşturun: Tüm sayıları asal çarpanlar olarak ifade ettiğimizde, ortak ve yaygın olmayan sayıları en büyük üsse yükseltilmiş olarak seçeceğiz. Daha sonra bunları tek bir matematiksel ifade olarak yazarsınız ve son olarak gerekli çarpma işlemlerini ve/veya kuvvetleri çözersiniz. Ve zaten lcm'nin sayısal değerine sahip olacaksınız.

Yöntem 3: Matematiksel formül

En küçük ortak katı elde etmenin son bir yolu vardır; bu, OBE'yi ve aşağıdaki matematiksel formülü kullanmaktan oluşur:

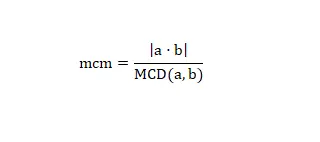
Bu formülü kullanarak herhangi bir sayının lcm'sini hesaplayabiliriz. Gerçek bir örnek görelim, eğer lcm'yi (2,6) hesaplamak istiyorsak, sadece (2 x 6) / 2 = 6 işlemini çözmemiz gerekir. Gördüğünüz gibi basit bir yöntem olduğu için hesaplamayı zaten çözmüş olacağız. ve GCD'niz varsa veya kolayca hesaplayabiliyorsanız hızlı .

LCM'yi hızlı bir şekilde hesaplamak için ipuçları

Az önce açıkladığımız üç yönteme hakim olduğunuzda, şimdi bahsedeceğimiz en küçük ortak katın özelliklerini okumanızı öneririz. Onlar sayesinde, daha önce açıklanan stratejileri kullanmak zorunda kalmadan, LCM'nin çok hızlı bir şekilde hesaplanabileceği bazı özel durumları tanımlayabileceksiniz.

• İlk sayı ikinciye bölünebilir: a ve b'nin en küçük ortak katını hesaplamak istiyorsak a, b'yi böldüğünde bu iki sayının ppcm'si en büyüğü olacaktır (bu durumda b). Örneğin, 2 ve 8'in lcm'sini hesaplamak istiyorsanız sonuç en büyüğü, dolayısıyla 8 olacaktır.
• İki asal sayı: İki asal sayı bulunması durumunda en hızlı yöntem bunları birbiriyle çarpmaktır ve sonuç ppcm olacaktır. Bu mantıklıdır, çünkü en büyük ortak böleni 1'dir; bu, sayıyı kendisinden daha basit faktörlere ayıramayacağımız ve bu nedenle onları yalnızca birbirleriyle çarpabileceğimiz anlamına gelir. Örneğin, 3 ve 5'in LCM'si çarpımlarının sonucu olacaktır: 3 x 5 = 15.

Kesirlerde en küçük ortak kat nasıl elde edilir?

Kesirlerde toplama veya çıkarma işlemini çözmek istediğimizde, lcm ile aynı olan ancak kesirlere uygulanan en küçük ortak paydayı hesaplamamız gerekir. Temel olarak, toplamı tek bir kesir olarak ifade edebilmek için iki paydanın lcm'sini arıyoruz. En küçük ortak paydanın reel kesir hesaplamasında nasıl uygulandığını görmek isterseniz bu bağlantıya girebilirsiniz.

Bilimsel hesap makinesinde Lcm

Herhangi bir bilimsel hesap makinesinde bulunan LCM anahtarı, iki tam sayının en küçük ortak katını hesaplamanıza olanak tanır. Casio hesap makineleri söz konusu olduğunda izlemeniz gereken sözdizimi veya prosedür aşağıdaki gibidir. İlk önce APHA + MCM'ye basarsınız (bu son tuş kahverengi olarak etiketlenecektir). Bu yapıldıktan sonra her iki sayıyı da girebilirsiniz ancak bunları virgülle ( SHIFT +, ) ayırmanız gerektiğini unutmayın. Son olarak eşittir butonuna tıklayarak en küçük ortak katı elde edeceksiniz.

LCM egzersizleri adım adım çözüldü

Daha sonra size adım adım çözülen en az ortak katların üç örneğini göstereceğiz. Bu şekilde bu sorunları çözmeye çalışabilir ve bu makalede anlattıklarımızdan biraz pratik yapabilirsiniz. Kavramları içselleştirmek istiyorsanız alıştırmaları çözmeye çalışmanız önemlidir çünkü teoriyi gerçeğe uygulamak gerekir. Bununla birlikte, egzersizlerle pratik yapmanıza izin veriyoruz:

4 ve 6'nın lcm'sini hesaplayın

6 ve 9'un lcm'sini hesaplayın

30 ve 40'ın lcm'sini hesaplayın