En küçük kareler yöntemi , bir dizi noktaya karşılık gelen en iyi düz çizgiyi bulmaya yönelik matematiksel bir araçtır. Bunu size basit bir şekilde açıklıyoruz:
Bir grafikte oraya buraya dağılmış bir sürü noktanız olduğunu hayal edin. Çizgi ile noktalar arasındaki mesafeyi en aza indirmek için bu noktalara en iyi “uyan” düz bir çizgiyi bulmak istiyorsunuz. En küçük kareler yönteminin arkasındaki fikir budur.
Yöntem, noktalar ile doğru arasındaki farkların karelerinin toplamını en aza indiren doğrunun denklemini hesaplamak için bir formül kullanır. Yani noktalardan en küçük “sapması” olan doğruyu arar.
Basit bir ifadeyle en küçük kareler yöntemi, bir araştırma sırasında elde edilen verilerin analizinde, davranışlarının doğrusal bir şekilde ifade edilmesi, çalınan bilgilerin hatalarının azaltılması amacıyla kullanışlıdır.
En küçük kareler yöntemini kim yarattı?
İstatistik ve veri analizinde temel bir araç olan en küçük kareler yöntemi, bunu 1794’te öneren Alman matematikçi Carl Friedrich Gauss’a atfedilir. Ancak Gauss, bunu 1809’a kadar yayınlamadı.
İlginç bir şekilde, Fransız matematikçi Andrien-Marie Legendre, 1805’te benzer bir versiyonunu bağımsız olarak geliştirerek yayınladı .
Modelleri gözlemlenen verilere uydurmak ve doğru tahminler yapmak için çeşitli disiplinlerde yaygın olarak kullanılan bu yöntemin oluşturulmasına her iki matematikçi de yardımcı oldu.
En küçük kareler formülü
Kuşkusuz bu yöntemin neler içerdiğini anlayabilmek için formülünü ve uygulanma sürecini anlatmak gerekir. En küçük kareler formülünün ayrıntılı bir açıklaması aşağıda verilmiştir:
Problemi tanımla
Diyelim ki, biri bağımsız değişken (x) ve biri bağımlı değişken (y) olmak üzere iki değişkenden oluşan bir veri setiniz var ve bu verilere düz bir çizgi sığdırmak istiyorsunuz.
Amaç, y’nin gerçek değerleri ile denklemin öngördüğü değerler arasındaki farkların karelerinin toplamını en aza indiren doğru denkleminin (kesme noktası ve eğim) katsayılarının değerlerini bulmaktır. takılı hat.
Doğrunun denklemini hesaplayın
Bir doğrunun denklemi y = mx + b biçimindedir; burada m eğim ve b y kesme noktasıdır. Myb değerlerini hesaplamak için en küçük kareler formülü şöyledir:
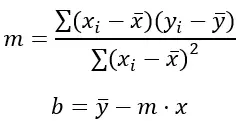
Altın:
Σ değerlerin toplamını temsil eder.
x i ve y i, her veri noktası için sırasıyla x ve y değişkenlerinin değerleridir.
x̄ ve ȳ sırasıyla x ve y değerlerinin ortalamalarıdır.
(x i – x̄) ve (y i – ȳ), x ve y değerleri ile bunların ortalamaları arasındaki farklardır.
(x i – x̄) 2, x’in değeri ile ortalaması arasındaki farkın karesidir.
sonuçları yorumlamak
Formülü kullanarak m ve b değerlerini hesapladıktan sonra bunları uygun çizginin denklemini elde etmek için kullanabilirsiniz. Örneğin, m = 2 ve b = 3’e sahipseniz, uygun çizginin denklemi y = 2x + 3 olacaktır. Bu, x’in farklı değerleri için y değerlerine ilişkin tahminler veya tahminler yapmanızı sağlar. düzeltilmiş sağa dayalıdır.
En küçük kareler yöntemi ne zaman kullanılır?
Muhtemelen kendinize bu yöntemin ne zaman kullanıldığını soracaksınız? Çeşitli durumlarda çok faydalıdır! Örneğin, bir ilişki veya eğilim bulmak için deneysel veya araştırma verilerini analiz etmek istediğinizde.
Diyelim ki bir evin fiyatı ile metrekare cinsinden büyüklüğü arasındaki ilişkiyi araştırıyorsunuz. Verilere en iyi uyan ve size bu ilişki hakkında net bir fikir veren düz çizgiyi bulmak için en küçük kareler yöntemini kullanabilirsiniz.
Aynı zamanda ekonomide ürün talebi veya fiyat davranışı gibi değişkenleri modellemek ve tahmin etmek için de kullanılır. Ek olarak mühendislikte matematiksel modellerin test veya simülasyon verilerine uygun hale getirilmesi için en küçük kareler yöntemi uygulanır.
En küçük kareler yöntemi, verileri analiz etmek ve önemli ilişkileri bulmak için birçok çalışma ve çalışma alanında kullanılan güçlü ve çok yönlü bir araçtır.
En küçük kareler yönteminin diğer teoremlerdeki uygulamaları
En küçük kareler yöntemi kendi başına kullanımının yanı sıra diğer teoremlerde de oldukça kullanışlıdır. Aşağıda konuya biraz daha bakalım.
Regresyon teoremi
Bir veri kümesine uyan en iyi doğruyu bulmak için regresyon teoreminde yaygın olarak kullanılır. Örneğin, bir bitkinin boyu ile aldığı ışık miktarı arasındaki ilişkiyi analiz etmek ve bitkinin farklı aydınlatma koşullarında nasıl büyüyeceğini belirlemek için bunu kullanabilirsiniz.
Teorem enterpolasyonu
Bu durumda, bir dizi noktaya en iyi uyan polinom fonksiyonunu bulmak için enterpolasyon teoreminde en küçük kareler yöntemi de uygulanır. Örneğin, konum ve zaman verilerine dayalı olarak hareket eden bir nesnenin yörüngesini yaklaşık olarak tahmin etmek için bunu kullanabilirsiniz.
Eğri uydurma teoremi
Bir veri kümesine uyan bir eğri bulmak için eğri uydurma teoreminde kullanılır. Bu, iklim değişikliğini tahmin etmek veya bir merminin yörüngesini tahmin etmek için iklim verilerinin modellenmesi gibi uygulamalarda faydalıdır.
Fourier analiz teoremi
Fourier analiz teoreminde, bir dizi ayrık veriden periyodik bir fonksiyona yaklaşmak için en küçük kareler yöntemi kullanılır. Bu, veri sinyalizasyonu ve görüntü ve ses sıkıştırma için geçerlidir.
Doğrusal Olmayan Regresyon Teoremi
Son olarak, doğrusal olmayan regresyon teoreminde , doğrusal bir ilişki izlemeyen bir veri kümesine uyan en iyi eğriyi bulmak için en küçük kareler yöntemi de uygulanır. Örneğin, bir kimyasalın konsantrasyonunun reaksiyon hızını nasıl etkilediğini analiz etmek için kullanabilirsiniz.
En küçük kareler yöntemi örneği
En küçük kareler yöntemini nasıl uygulayabileceğinizi daha iyi anlamak için aşağıdaki bir örneğe bakalım.
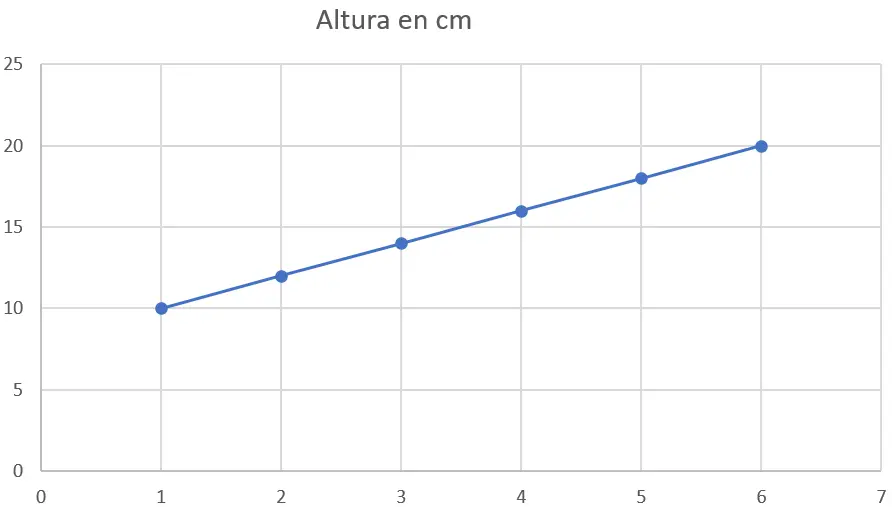
Bir bitkinin farklı haftalardaki aşağıdaki yükseklik verilerine (santimetre cinsinden) sahip olduğunuzu varsayalım:
| Hafta | santimetre cinsinden yükseklik |
| 1 | on |
| 2 | 12 |
| 3 | 14 |
| 4 | 16 |
| 5 | 18 |
| 6 | yirmi |
Gelecekteki tesis boyu hakkında tahminde bulunmak için bu verilere uyan en iyi düz çizgiyi bulmak istiyorsunuz.
Adım 1 : Verilerin grafiğini çizin
Yapılacak ilk şey, verileri bir dağılım grafiğine çizmektir. X ekseni haftaları, y ekseni ise santimetre cinsinden yüksekliği temsil edecektir. İşte grafik:
Adım 2 : En küçük kareler yöntemini uygulayın
En küçük kareler yöntemi, gerçek veriler ile doğrunun tahmin ettiği değerler arasındaki farkların karelerinin toplamını en aza indiren bir doğru bulmayı amaçlamaktadır. Bu durumda çizgi, bir doğrunun denklemi ile temsil edilir: y = mx + b, burada “y” yükseklik, “x” haftalar, “m” çizginin eğimi ve “b” ise y-kesişim noktası.
Farkların kareleri toplamını en aza indiren “m” ve “b” değerlerini bulmak için aşağıdaki formüller kullanılır:
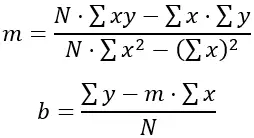
N, veri noktalarının sayısı (bu durumda, 6) olduğunda, Σxy hafta çarpı yüksekliklerin toplamıdır, Σx haftaların toplamıdır, Σy yüksekliklerin toplamıdır ve Σx 2 haftaların karelerinin toplamıdır .
Bu formülleri yükseklik verilerine uygulayarak şunu elde ederiz:
Σxy = 1 10 + 2 12 + 3 14 + 4 16 + 5 18 + 6 20 = 630
Σx = 1 + 2 + 3 + 4 + 5 + 6 = 21
Σy = 10 + 12 + 14 + 16 + 18 + 20 = 90
Σx 2 = 1 2 + 2 2 + 3 2 + 4 2 + 5 2 + 6 2 = 91
Bu değerleri “m” ve “b” formüllerinde yerine koyarsak:
m = (6 · 630 – 21 · 90) ÷ (6 · 91 – 21 2 ) ≈ 2,07
b = (90 – 2,07 · 21) ÷ 6 ≈ 3,24
Dolayısıyla yükseklik verilerine karşılık gelen doğrunun denklemi: y’dir.