Elipsin dışmerkezliğini hesaplama

Bu sayfada elipsin dışmerkezliğinin anlamını ve nasıl hesaplandığını (formül) bulacaksınız. Ek olarak elips dışmerkezliği hesaplamalarının örneklerini göreceksiniz.

Elipsin dışmerkezliği nedir?

Elips dışmerkezliği, bir elipsin ne kadar yuvarlak veya düz olduğunu ölçen bir parametredir, yani bir elipsin dışmerkezliği, elipsin bir daireye ne kadar benzediğini gösterir.

Öte yandan elipsin nelerden oluştuğunu da hatırlayalım: Elips, bir düzlemin diğer iki sabit noktaya (F ve F’ odakları olarak adlandırılan) uzaklıkları toplamı sabit olan tüm noktalarının geometrik yeridir .

Elips Eksantriklik Formülü

Elipsin dışmerkezliğinin tanımını gördükten sonra, formülünden nasıl hesaplandığına bakalım:

Elipsin dışmerkezlik formülü aşağıdaki gibidir:

$e=\cfrac{c}{a}$

Altın:

$e$

elipsin dışmerkezliğidir
$c$

elipsin odağından (F ve F’ noktaları) merkeze olan mesafedir
$a$

elipsin yarı ana (veya ana) ekseninin uzunluğudur.

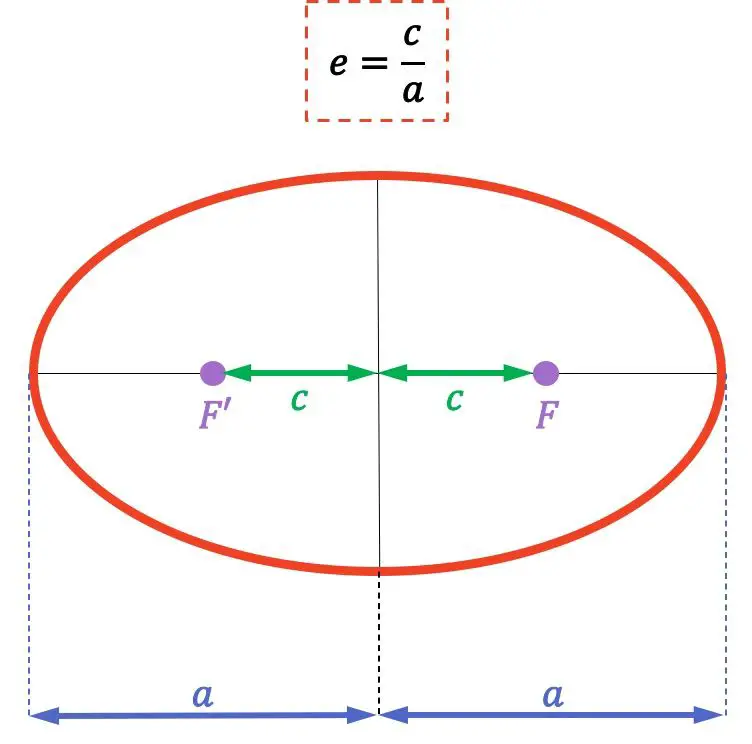
Bir elipsin odak noktalarının, elipsin herhangi bir noktasına olan uzaklıklarının toplamı sabit olan sabit noktalar olduğunu unutmayın. Ayrıca iki odak noktası arasındaki mesafeye odak uzaklığı denir.

Eksantriklik değeri, mükemmel bir daire anlamına gelen sıfır ile yatay bir çizgi anlamına gelen bir arasında değişir. Açıkçası 0 ve 1 dahil edilmemiştir çünkü sonuçta ortaya çıkan geometrik nesneler artık elips değildir.

$0 Par conséquent, comme vous pouvez le voir dans la représentation graphique ci-dessous, plus la valeur de l'excentricité de l'ellipse est petite, plus elle ressemble à un cercle, au contraire, plus le coefficient est grand, plus l'ellipse est aplatie. <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="https://mathority.org/wp-content/uploads/2023/07/excentricite-dellipse.webp" alt="valeur de l'excentricité de l'ellipse" class="wp-image-2095" width="669" height="154" srcset="" sizes=""></figure> </div> <p> En bref, l’excentricité d’une ellipse est un coefficient dont la valeur détermine la forme qu’elle a. </p> <div class="adsb30" style=" margin:12px; text-align:center"> <div id="ezoic-pub-ad-placeholder-109"></div> </div> <p> Si vous êtes plus intéressé par les caractéristiques d’une ellipse, vous pouvez vous référer à l’ <a href="https://mathority.org/equation-de-la-formule-de-l'ellipse/">équation de l’ellipse</a> . Sur cette page, vous trouverez une explication détaillée de ce qu’est une ellipse, de tous ses éléments et de la façon dont son équation est calculée. Et, en plus, vous pourrez voir plusieurs exemples, exercices et problèmes résolus sur des ellipses. </p> <h2 class="wp-block-heading"><span class="ez-toc-section" id="relacion-importante-para-hallar-la-excentricidad-de-la-elipse"></span> Relation importante pour trouver l’excentricité de l’ellipse<span class="ez-toc-section-end"></span></h2> <p> Les différents éléments d’une ellipse sont liés les uns aux autres. De plus, les relations entre eux sont très importantes pour les exercices sur les ellipses, car elles sont généralement nécessaires pour résoudre des problèmes sur les ellipses et déterminer leurs équations. Comme nous l’avons vu plus haut dans l’explication de la notion d’excentricité de l’ellipse, la distance de tout point de l’ellipse au foyer F plus la distance du même point au foyer F’ est constante. Eh bien, cette valeur constante est égale à deux fois ce que mesure le demi-grand axe. Autrement dit, l’égalité suivante vaut pour tout point d’une ellipse :” title=”Rendered by QuickLaTeX.com” height=”478″ width=”3899″ style=”vertical-align: -4px;”></p> <p> d(P,F) + d(P,F’)= 2a</p> <p class=$ $Où$

d(P,F)

$et$

d(P,F’)

$est la distance du point P au foyer F et F' respectivement et$

sahip olmak

$est la longueur de l'axe semi-focal. Par conséquent, puisque le sommet de l'axe secondaire est juste au milieu de l'axe principal, la distance de celui-ci à l'un des foyers est équivalente à la longueur du demi-axe principal ($

sahip olmak

$): <div class="wp-block-image"> <figure class="aligncenter size-large is-resized"><img decoding="async" loading="lazy" src="https://mathority.org/wp-content/uploads/2023/07/relation-delements-dellipse.webp" alt="équation de preuve d'ellipse" class="wp-image-2087" width="332" height="197" srcset="" sizes=""></figure> </div> <p> Par conséquent, à partir du théorème de Pythagore, il est possible de trouver <strong>la relation qui existe entre le demi-axe principal, le demi-axe secondaire et la distance semi-focale d’une ellipse :</strong>” title=”Rendered by QuickLaTeX.com” height=”195″ width=”582″ style=”vertical-align: -5px;”></p> <p> a^2=b^2+c^2</p> <p class=$ $Retenez également cette autre formule car elle vous sera très utile pour calculer le résultat des exercices avec des ellipses. <h2 class="wp-block-heading"><span class="ez-toc-section" id="ejemplo-de-como-calcular-la-excentricidad-de-la-elipse"></span> Exemple de calcul de l’excentricité de l’ellipse<span class="ez-toc-section-end"></span></h2> <p> Vous trouverez ci-dessous un exercice résolu pour voir comment l’excentricité d’une ellipse est calculée :</p> <ul> <li> Trouver l’excentricité de l’ellipse dont le demi-grand axe et le demi-grand axe mesurent respectivement 5 et 3 unités.</li> </ul> <p> Pour trouver la valeur de l’excentricité de l’ellipse, il faut connaître la longueur du demi-axe principal et la longueur du segment entre un foyer et le centre de l’ellipse. Nous connaissons déjà le premier, nous n’avons donc qu’à déterminer la distance semi-focale. A partir de la formule de la relation entre les éléments d’une ellipse, on peut calculer combien vaut la demi-distance focale : ” title=”Rendered by QuickLaTeX.com” height=”193″ width=”2952″ style=”vertical-align: -5px;”></p> <p> a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{5^2-3^2}=\sqrt {16} = 4</p> <p class=$ $Et quand on connaît déjà la valeur des termes$