Burada elips denkleminin (formülünün) merkezi orijine sahip olsun ya da olmasın nasıl hesaplandığını bulacaksınız. Ayrıca elipsin elemanlarının neler olduğunu, nasıl hesaplanacağını ve ne için kullanıldıklarını da bulacaksınız. Ayrıca elips denklemlerinin örneklerini ve çözülmüş alıştırmalarını görebileceksiniz.
Elips denklem formülü
Elipsin Kartezyen koordinatlardaki denkleminin formülü şöyledir:
![]()
Altın:
-

Ve

elipsin merkezinin koordinatları şunlardır:
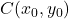
-

elipsin yatay yarıçapıdır.
-

elipsin dikey yarıçapıdır.
Orijin merkezli elipsin denklemi
Çok yaygın bir elips türü, merkezi koordinatların başlangıç noktasında, yani (0,0) noktasında olan elipstir. Bu yüzden orijin merkezli elipsin denklemini nasıl bulacağımızı göreceğiz.
Elips denkleminin formülünü takip ederek:
![]()
Elips koordinatların orijininde ortalanıyorsa bu şu anlama gelir:
![]()
Ve
![]()
0’a eşit olduğundan denkleminiz şöyle olacaktır:
![]()
Bu ifadeye elipsin kanonik denklemi veya indirgenmiş denklemi adını da veren matematikçiler vardır.
elipsin elemanları
Elipsin denkleminin neye benzediğini gördükten sonra elemanlarının ne olduğunu göreceğiz. Ama önce elipsin tam olarak ne olduğunu hatırlayalım:
Elips, çevreye çok benzeyen düz, kapalı, kavisli bir çizgidir ancak şekli daha ovaldir. Özellikle elips, bir düzlemin diğer iki sabit noktaya (F ve F’ odakları olarak adlandırılan) uzaklıklarının toplamı sabit olan tüm noktalarının geometrik yeridir.
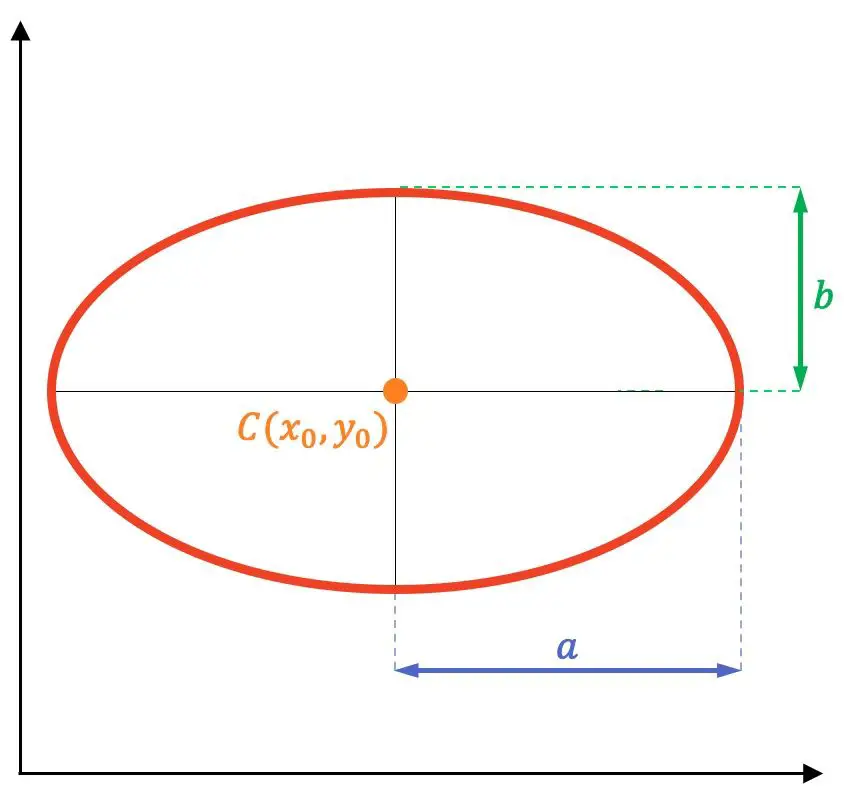
Buna göre bir elipsin elemanları şunlardır:
- Odaklar : bunlar sabit F ve F’ noktalarıdır (aşağıdaki resimde mor renkli noktalar). Elips üzerindeki herhangi bir nokta ile her bir odak noktası arasındaki mesafelerin toplamı, elips üzerindeki tüm noktalar için sabittir.
- Ana veya odak ekseni : bu, odağın bulunduğu elipsin simetri eksenidir. Ana eksen olarak da adlandırılır.
- İkincil eksen : Bu, elipsin asal eksene dik simetri eksenidir. Aynı zamanda küçük eksen olarak da adlandırılır ve odakları birleştiren segmentin dik açıortayına karşılık gelir.
- Merkez : elipsin eksenlerinin kesişme noktasıdır. Ayrıca elipsin simetri merkezidir (grafikteki turuncu nokta).
- Köşeler : elipsin simetri eksenleriyle kesişme noktaları (siyah noktalar).
- Yarı ana eksen veya asal eksen: Elipsin merkezinden asal eksenin köşelerine giden bölüm.
- Yarı küçük eksen veya ikincil eksen: elipsin merkezi ile ikincil eksenin köşeleri arasındaki bölüm.
- Odak Uzaklığı : İki odak noktası arasındaki mesafedir.
- Yarı odak mesafesi : merkez ile odak noktalarının her biri arasındaki mesafeye karşılık gelir.
- Radyo vektörleri : elipsin herhangi bir noktasını her odağa birleştiren bölümlerdir (grafikteki mavi bölümler).

Bir elipsin elemanları arasındaki ilişki
Bir elipsin farklı elemanları birbirine bağlıdır. Ayrıca elipslerle ilgili çalışmalarda aralarındaki ilişkiler çok önemlidir, çünkü genellikle elipslerle ilgili problemlerin çözümünde ve denklemlerinin belirlenmesinde gereklidir.
Yukarıda elipsin tanımında gördüğümüz gibi, elipsin herhangi bir noktasından F odağına olan mesafe artı aynı noktadan F’ odağına olan mesafe sabittir. Bu sabit değer yarı ana eksenin ölçtüğünün iki katına eşittir. Başka bir deyişle, bir elips üzerindeki herhangi bir nokta için aşağıdaki eşitlik geçerlidir:
![]()
Altın
![]()
Ve
![]()
P noktasından sırasıyla F ve F’ odağına olan mesafedir ve
![]()
yarı odak ekseninin uzunluğudur.
Bu nedenle, ikincil eksenin tepe noktası odak ekseninin tam ortasında olduğundan, odaklardan birine olan mesafe yarı birincil eksenin uzunluğuna eşdeğerdir (
![]()
):
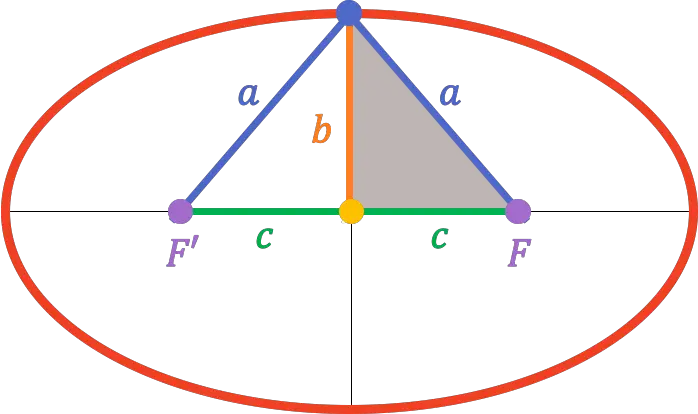
Böylece, Pisagor teoreminden , ana yarı eksen, ikincil yarı eksen ve yarı odak uzaklığı arasında var olan ilişkiyi bulmak mümkündür:
![]()
Bu formülü unutmayın çünkü elipslerle yapılan egzersizlerin sonuçlarını hesaplamak için çok faydalı olacaktır.
Elips eksantrikliği
Açıkçası, tüm elipsler aynı değildir, ancak bazıları daha uzun, bazıları ise daha düzdür. Yani belirli bir elipsin ne kadar yuvarlak olduğunu ölçmek için kullanılan bir katsayı vardır. Bu katsayıya dışmerkezlik denir ve aşağıdaki formülle hesaplanır:
![]()
Altın
![]()
elipsin merkezinden odak noktalarından birine olan mesafedir ve
![]()
yarı ana eksenin uzunluğu.
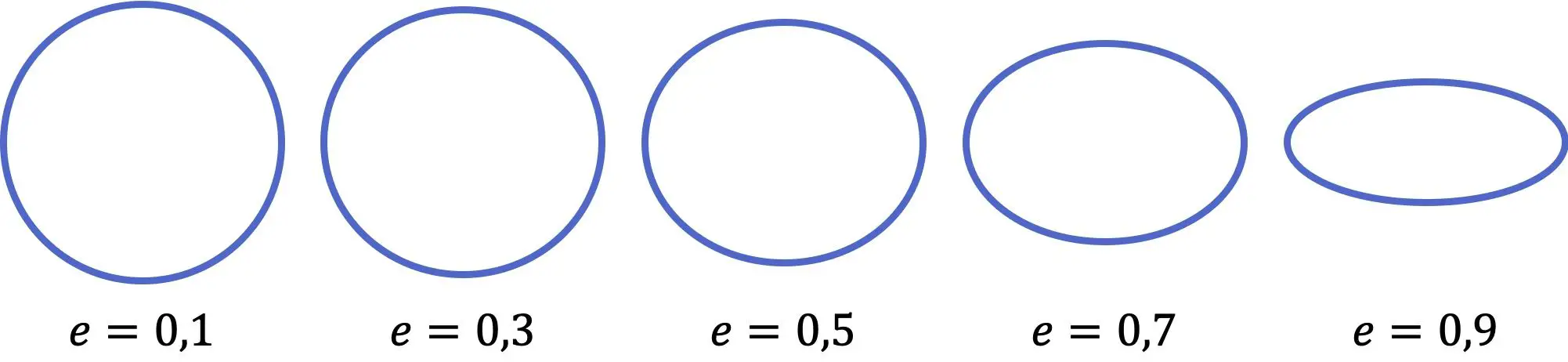
Önceki gösterimde görebileceğiniz gibi, elipsin dışmerkezlik değeri ne kadar küçük olursa, daireye o kadar benzer, katsayı ne kadar büyükse elips o kadar düzleşir. Ek olarak, dışmerkezlik değeri sıfırdan (mükemmel daire) bire (yatay çizgi) kadar değişir ve her ikisi de dahil değildir.

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-4)^2}{5^2 }+\cfrac{(y-(-1))^2}{3^2} = 1\cfrac{\bm{(x-4)^2}}{\bm{25}}+\cfrac{\ bm{(y+1)^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-2)^2}{6^2}+\cfrac{(y-0)^2}{3^2} = 1\cfrac{\bm{(x-2)^2}} {\bm{36}}+\cfrac{\bm{y^2}}{\bm{9}} \bm{= 1}

![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{13^2 }+\cfrac{(y-0)^2}{12^2} = 1\cfrac{\bm{x^2}}{\bm{169}}+\cfrac{\bm{y^2}} {\bm{144}} \bm{= 1}

![]()
d_v=6-(-4) =10 b =\cfrac{10}{2} = 5
![]()
C_x= \cfrac{10+(-4)}{2} = \cfrac{6}{2} =3 C_y= \cfrac{6+(-4)}{2} = \cfrac{2}{ 2} = 1C(3.1)
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-3)^2}{7^2 }+\cfrac{(y-1)^2}{5^2} =1\cfrac{\bm{(x-3)^2}}{\bm{49}}+\cfrac{\bm{( y-1)^2}}{\bm{25}} \bm{= 1}
![]()
a^2=b^2+c^2 c^2=a^2-b^2 c=\sqrt{a^2-b^2} = \sqrt{7^2-5^2}=\sqrt {24}
![]()
\sqrt{24}
![]()
C(3,1) \bm{F\left(3+\sqrt{24},1}\right)} \bm{F\left(3-\sqrt{24},1}\right)}

![]()
d(P,F) + d(P,F’)= 2a 3+5= 2a 8= 2a \cfrac{8}{2}= a 4= a
![]()
a^2=b^2+c^2 b^2=a^2-c^2 b=\sqrt{a^2-c^2} = \sqrt{4^2-3^2}=\sqrt {7}
![]()
\cfrac{(x-x_0)^2}{a^2}+\cfrac{(y-y_0)^2}{b^2} = 1\cfrac{(x-0)^2}{4^2 }+\cfrac{(y-0)^2}{\left(\sqrt{7}\right)^2} =1\cfrac{\bm{x^2}}{\bm{16}}+\ cfrac{\bm{y^2}}{\bm{7}} \bm{= 1}$
Son olarak bu makale sizin için yararlı olduysa hiperbol formülü ve parabol formülü ile ilgili sayfalarımız da mutlaka ilginizi çekecektir. Hiperbol ve parabolün ne olduğu, denklemleri, özellikleri, örnekleri, çözülmüş alıştırmalar hakkında ayrıntılı bir açıklama bulacaksınız…