Düzlemin parametrik denklemleri

Bu sayfada bir planın parametrik denklemlerinin ne olduğunu ve nasıl hesaplandıklarını (formül) bulacaksınız. Ayrıca örnekleri görebilecek ve adım adım çözülen alıştırmalarla pratik yapabileceksiniz.

Bir düzlemin parametrik denklemleri nelerdir?

Analitik geometride bir düzlemin parametrik denklemleri , herhangi bir düzlemin matematiksel olarak ifade edilmesini sağlayan denklemlerdir. Bir düzlemin parametrik denklemlerini bulmak için yalnızca bir noktaya ve o düzleme ait iki doğrusal bağımsız vektöre ihtiyacımız var.

Planın parametrik denklemlerinin formülasyonu

Bir düzlemin bir nokta ve iki yön vektörünü düşünün:

$\begin{array}{c} P(P_x,P_y,P_z) \\[2ex] \vv{\text{u}}=(\text{u}_x,\text{u}_y,\text{u}_z)\\[2ex] \vv{\text{v}}=(\text{v}_x,\text{v}_y,\text{v}_z)\end{array}$

Bir düzlemin parametrik denklemlerinin formülü şöyledir:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Altın

$\lambda$

$\mu$

iki skalerdir, yani iki gerçek sayıdır.

Düzlem denkleminin iki yön vektörünün doğrusal olarak bağımsız olması, yani farklı (paralel olmayan) yönlere sahip olması önemlidir. Aksi takdirde yukarıdaki denklem hiçbir planı temsil etmez.

Öte yandan, parametrik denklemin yanı sıra, uzaydaki bir düzlemi (R3’te) analitik olarak ifade etmenin genel düzlem denklemi gibi başka yollarının da olduğunu unutmayın. Bu linkte formülünü, planın parametrik denklemlerinden nasıl hesaplandığını, örneklerini ve çözülmüş alıştırmaları bulacaksınız.

Bir düzlemin parametrik denklemlerinin nasıl bulunacağına ilişkin örnek

Düzlemin parametrik denkleminin ne olduğunu gördükten sonra, bir örnekle nasıl hesaplandığına bakalım:

Noktadan geçen düzlemin parametrik denklemlerini bulun
$P(1,3,2)$

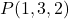
ve vektörleri içerir

$\vv{\text{u}}=(2,0,-1)$

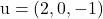
Ve

$\vv{\text{v}}=(4,2,3)$

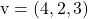
Planın parametrik denklemlerini belirlemek için formülünü uygulamanız yeterlidir:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Şimdi noktayı ve her yön vektörünü denklemde yerine koyuyoruz:

$\displaystyle \begin{cases}x=1 + \lambda \cdot 2 + \mu \cdot 4 \\[1.7ex] y=3+ \lambda \cdot 0 + \mu \cdot 2\\[1.7ex] z=2 + \lambda\cdot (-1)+ \mu \cdot 3\end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + 2\lambda + 4\mu } \\[1.7ex] \bm{y=3 + 2\mu}\\[1.7ex] \bm{z=2 -\lambda+ 3\mu} \end{cases}$

Bir düzlemin vektör denkleminden parametrik denklemlere nasıl geçilir?

Bir düzlemin parametrik denklemlerini belirlemenin bir başka yöntemi, bir düzlemin vektör denklemidir. Aşağıda demoyu görebilirsiniz.

Herhangi bir düzlemin vektör denklemi şöyle olsun:

$(x,y,z)=(P_x,P_y,P_z)+\lambda (\text{u}_x,\text{u}_y,\text{u}_z) + \mu (\text{v}_x,\text{v}_y,\text{v}_z)$

Vektörlerin çarpımlarını skalerlerle çalıştırıyoruz ve ilk önce gerçekleştiriyoruz:

$(x,y,z)=(P_x,P_y,P_z)+ (\lambda\text{u}_x,\lambda\text{u}_y,\lambda\text{u}_z) +(\mu\text{v}_x,\mu\text{v}_y,\mu\text{v}_z)$

Daha sonra bileşenleri ekliyoruz:

$(x,y,z)=(P_x+\lambda \text{u}_x + \mu \text{v}_x,P_y+\lambda \text{u}_y + \mu \text{v}_y,P_z+\lambda \text{u}_z + \mu \text{v}_z)$

Ve son olarak, her değişkene karşılık gelen koordinatları ayrı ayrı özümleyerek düzlemin parametrik denklemini elde ediyoruz:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y\\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Yukarıdaki iki örnekte görebileceğiniz gibi bir düzlemin parametrik denklemlerini bulmak nispeten kolaydır. Bununla birlikte, problemler biraz karmaşıklaşabilir, bu nedenle aşağıda farklı zorluk derecelerinde birkaç çözülmüş alıştırma bulacaksınız, böylece pratik yapabilirsiniz.

Düzlemin parametrik denklemlerinin çözülmüş problemleri

1. Egzersiz

Vektörü içeren düzlemin parametrik denklemlerini belirleyin

$\vv{\text{u}}=(2,1,5)$

ve aşağıdaki iki noktadan geçer:

$A(3,2,-1)$

$B(-2,-1,1).$

Çözüme bakın

Bir düzlemin denklemini bilmek için bir noktaya ve iki vektöre ihtiyacınız vardır ve bu durumda elimizde yalnızca bir vektör vardır, dolayısıyla düzlemin başka bir yönlendirici vektörünü bulmamız gerekir. Bunu yapmak için düzlemin iki noktasını tanımlayan vektörü hesaplayabiliriz:

$\vv{AB} = B - A = (-2,-1,1) - (3,2,-1) = (-5,-3,2)$

Artık düzlemin iki yön vektörünü ve bir noktayı zaten bildiğimize göre, düzlemin parametrik denklemleri için formülü kullanıyoruz:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Ve iki vektörü ve düzlemdeki iki noktadan birini denklemde yerine koyarız:

$\displaystyle \begin{cases}x=3 + \lambda \cdot 2+ \mu \cdot (-5) \\[1.7ex] y=2 + \lambda \cdot 1 + \mu \cdot (-3) \\[1.7ex] z=(-1) + \lambda\cdot 5 + \mu \cdot 2 \end{cases}$

$\displaystyle \begin{cases}\bm{x=3 +2 \lambda-5\mu } \\[1.7ex] \bm{y=2 + \lambda-3 \mu } \\[1.7ex] \bm{z=-1 + 5\lambda + 2\mu } \end{cases}$

Alıştırma 2

Aşağıdaki üç noktayı içeren düzlemin parametrik denklemlerini bulun:

$A(4,1,0) \qquad B(2,-3,-1) \qquad C(1,5,3)$

Çözüme bakın

Düzlemin parametrik denklemlerini bulmak için düzlemde birbirine bağlanan iki doğrusal bağımsız vektör bulmamız gerekir. Bunun için de 3 noktayla tanımlanan iki vektörü hesaplayabiliriz:

$\vv{AB} = B - A = (2,-3,-1) - (4,1,0) = (-2,-4,-1)$

$\vv{AC} = C - A = (1,5,3) - (4,1,0) = (-3,4,3)$

Bulunan iki vektörün koordinatları orantılı olmadığından birbirlerinden doğrusal olarak bağımsızdırlar.

Artık iki yön vektörünü ve düzlemdeki bir noktayı zaten bildiğimize göre, düzlemin parametrik denklemi formülünü uyguluyoruz:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

Ve iki vektörü ve düzlemin üç noktasından birini denklemde yerine koyarız:

$\displaystyle \begin{cases}x=4 + \lambda \cdot (-2)+ \mu \cdot (-3) \\[1.7ex] y=1 + \lambda \cdot (-4) + \mu \cdot 4 \\[1.7ex] z=0 + \lambda\cdot (-1) + \mu \cdot 3 \end{cases}$

$\displaystyle \begin{cases}\bm{x=4 -2 \lambda-3\mu } \\[1.7ex] \bm{y=1-4 \lambda+4 \mu } \\[1.7ex] \bm{z=-\lambda + 3\mu } \end{cases}$

Alıştırma 3

Aşağıdaki vektör denklemiyle tanımlanan düzlemin parametrik denklemlerini hesaplayın:

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

Çözüme bakın

Düzlemin vektör denklemini parametrik bir denkleme dönüştürmek için koordinatlarla işlem yapmanız ve ardından her değişkeni ayrı ayrı çözmeniz gerekir:

$(x,y,z)=(0,-1,5)+\lambda (6,1,-2) + \mu (1,-1,3)$

$(x,y,z)=(0,-1,5)+(6\lambda,\lambda,-2\lambda) + (\mu,-\mu,3\mu)$

$(x,y,z)=(6\lambda+\mu,-1+\lambda-\mu,5-2\lambda+3\mu)$

$\displaystyle \begin{cases}\bm{x=6\lambda+\mu } \\[1.7ex] \bm{y=-1+\lambda-\mu} \\[1.7ex] \bm{z=5-2\lambda+3\mu } \end{cases}$

Alıştırma 4

Doğruyu içeren düzlemin parametrik denklemlerini bulun

$r$

ve sağa paralel

$s.$

çizgiler olmak üzere:

$\displaystyle r: \ \begin{cases} x=1+t \\[1.7ex] y=2-3t\\[1.7ex] z=4+2t \end{cases} \qquad \qquad s: \ \frac{x-4}{2} = \frac{y+3}{2}= \frac{z-2}{-3}$

Çözüme bakın

Düzlemin parametrik denklemlerini bulmak için iki yön vektörünü ve düzlem üzerindeki bir noktayı bilmemiz gerekir. Talimat bize satırı içerdiğini söylüyor

$r$

Dolayısıyla düzlemi tanımlamak için yön vektörünü ve bu doğru üzerindeki bir noktayı alabiliriz. Ayrıca bu ifade bize düzlemin doğruya paralel olduğunu söyler.

$s,$

yani bu doğrunun yön vektörünü düzlem denklemi için de kullanabiliriz.

doğru

$r$

parametrik denklemler biçiminde ifade edilir, dolayısıyla yön vektörünün bileşenleri parametre terimlerinin katsayılarıdır.

$t:$

$\vv{r} =(1,-3,2)$

Aynı çizgi üzerindeki bir noktanın Kartezyen koordinatları da parametrik denklemlerin bağımsız terimleridir:

$P(1,2,4)$

Öte yandan düz çizgi

$s$

yön vektörünün bileşenleri kesirlerin paydaları olacak şekilde sürekli bir denklem biçimindedir:

$\vv{s} =(2,2,-3)$

Bu nedenle planın parametrik denklemleri şöyledir:

$\displaystyle \begin{cases}x=P_x + \lambda \text{u}_x + \mu \text{v}_x \\[1.7ex] y=P_y + \lambda \text{u}_y + \mu \text{v}_y \\[1.7ex] z=P_z + \lambda\text{u}_z + \mu \text{v}_z \end{cases}$

$\displaystyle \begin{cases}x=1 + \lambda \cdot 1+ \mu \cdot 2 \\[1.7ex] y=2 + \lambda \cdot (-3) + \mu \cdot 2 \\[1.7ex] z=4 + \lambda\cdot 2 + \mu \cdot (-3) \end{cases}$

$\displaystyle \begin{cases}\bm{x=1 + \lambda+2\mu } \\[1.7ex] \bm{y=2-3 \lambda+2 \mu } \\[1.7ex] \bm{z=4+2\lambda -3\mu } \end{cases}$

Bir düzlemin parametrik denklemleri nelerdir?

Planın parametrik denklemlerinin formülasyonu

Bir düzlemin parametrik denklemlerinin nasıl bulunacağına ilişkin örnek

Bir düzlemin vektör denkleminden parametrik denklemlere nasıl geçilir?

Düzlemin parametrik denklemlerinin çözülmüş problemleri

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Yorum bırakın Yanıtı iptal et