Düzenli veya tersinir matris

Bu sayfada normal veya tersinir bir matrisin açıklamasını ve bir matrisin tersinin ne zaman yapılıp ne zaman yapılamayacağını nasıl bileceğinizi bulacaksınız. Ek olarak, kavramı tam olarak anlamak için düzenli matrislerin birkaç örneğini de göreceksiniz ve son olarak size bu tür matrislerin tüm özelliklerini göstereceğiz.

Düzenli matris nedir?

Düzenli bir matrisin tanımı aşağıdaki gibidir:

Düzenli bir matris, ters çevrilebilen, yani söz konusu matrisin tersi hesaplanabilen bir kare matristir. Bu nedenle determinantı sıfırdan farklıdır (0).

Düzenli matrislere aynı zamanda tersinir, tekil olmayan veya dejenere olmayan matrisler de denir.

Normal matrisin karşıt matrisi tekil veya dejenere matristir.

Dolayısıyla bir matrisin ne zaman düzenli ya da tekil olduğunu, yani bir matrisin ne zaman tersinin alınıp alınamayacağını bilmek için matrisin determinantını çözmek yeterlidir:

Matrisin determinantı sıfırdan farklı ise matris düzenli veya tersinirdir.

Matrisin determinantı sıfıra eşitse matris tekildir veya tersinir değildir.

Sonuç olarak, bir matrisin determinantını hesaplamak, matrisin tersi olup olmadığını bilmenin en basit yoludur, dolayısıyla herhangi bir matrisin tersinirliğini belirlemek için önerdiğimiz şey budur.

Bir matrisin nasıl ters çevrileceğini öğrenmek istiyorsanız, bir matrisin nasıl ters çevrileceğini adım adım açıklayan ters matris formülüne göz atabilirsiniz ve ayrıca birkaç örnek ve pratik yapmak için çözülmüş alıştırmalar bulacaksınız.

Düzenli veya tersinir matris örnekleri

Düzenli veya tersinir matrisin anlamını gördükten sonra, farklı boyutlardaki düzenli matrislerin bazı örneklerini görelim:

Normal veya tersinir 2×2 matris örneği

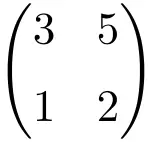
Determinantını hesaplayarak bunun düzenli bir matris olduğunu doğrulayabiliriz:

$\displaystyle\begin{vmatrix} 3&5 \\[1.1ex] 1 & 2\end{vmatrix}=1\bm{\neq 0}$

2. mertebeden matrisin determinantı 0’dan farklı olduğundan normal bir matristir.

Normal veya tersinir 3×3 matris örneği

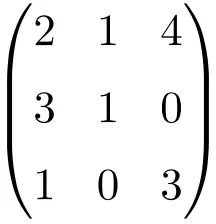
3x3 boyutlu normal veya tersinir matris örneği

Tersine çevrilebilir bir matris olduğunu doğrulamak için matrisin determinantını yapmalıyız:

$\displaystyle\begin{vmatrix} 2&1&4\\[1.1ex] 3&1&0\\[1.1ex] 1&0&3\end{vmatrix}=-7\bm{\neq 0}$

3. mertebeden matrisin determinantı 0’dan farklı bir sonuç verdiğinden normal bir matristir.

Normal veya ters çevrilebilir 4 × 4 matris örneği

4x4 boyutlu normal veya tersinir matris örneği

Matrisin determinantını almak onun düzenli bir matris olduğunu gösterir:

$\displaystyle\begin{vmatrix} 1&3&-2&0\\[1.1ex] 2&-1&0&5\\[1.1ex] 1&3&1&2\\[1.1ex] 0&-1&2&4\end{vmatrix}=-49\bm{\neq 0}$

4. mertebeden matrisin determinantı sıfır değildir, dolayısıyla tersinir bir matristir.

Uyarı: Eğer determinant hesaplamaları konusunda şüpheleriniz varsa determinant nasıl hesaplanır sayfasına bakabilirsiniz.

Düzenli veya tersinir matrislerin özellikleri

Düzenli veya tersinir matrisler doğrusal cebir için çok önemlidir ve bunun nedeni aşağıdaki özelliklerdir:

Eğer A tersinir bir matris ise, onun transpoze veya transpoze matrisi de öyledir. Ek olarak, devriğin ters matrisi, tersin devriğine eşittir.

$\displaystyle \left(A^t\right)^{-1}=\left(A^{-1}\right)^t$

Düzenli bir matrisin aralığı her zaman mümkün olan maksimumdur veya başka bir deyişle aralık, matrisin boyutuna eşdeğerdir.

Tersine çevrilebilir iki matris arasındaki matris çarpımı başka bir düzenli matrise yol açar. Bu durum belirleyicilerin özellikleriyle kolaylıkla gösterilebilir:

$\displaystyle \left.\begin{array}{l}\text{det}(A\cdot B)=\text{det}(A)\cdot\text{det}(B) \\[2ex] \text{det}(A)\neq 0 \quad ; \quad \text{det}(B) \neq 0 \end{array}\right\} \longrightarrow \ \text{det}(A\cdot B) \neq 0$

Her ortogonal matris aynı zamanda düzenli bir matristir.

A, bir doğrusal denklem sistemini temsil eden matris olsun
$(Ax=b)$

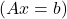
A düzenli bir matris ise sistemin tek bir çözümü vardır, dolayısıyla uyumlu bir determinant sistemidir (SCD).

Ayrıca sistem homojen bir sistem ise
$(Ax=0)$

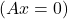
ve A ters çevrilebilir, sistemin çözümü önemsizdir:

$x=0.$

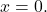
Normal bir matrisin sütunları ve satırları birbirlerinden doğrusal olarak bağımsızdır.

Düzenli veya ters çevrilebilir bir matrisin tüm özdeğerleri (veya özdeğerleri) sıfır değildir.

Düzenli altın tersine çevrilebilir matris