Doğrusal fonksiyon ve afin fonksiyon -

Bu makalede afin fonksiyon ve doğrusal fonksiyonun açıklamasını ve bu iki fonksiyon türü arasındaki farkları bulacaksınız. Ek olarak, bir afin fonksiyonun ve bir doğrusal fonksiyonun grafiğinin nasıl çizileceğine ve bunların ifadelerinin iki noktadan nasıl hesaplanacağına ilişkin örnekler göreceksiniz. Son olarak, adım adım çözülen çeşitli egzersizlerle antrenman yapabileceksiniz.

Afin fonksiyon ve doğrusal fonksiyon nedir?

Afin fonksiyonun ve doğrusal fonksiyonun tanımları aşağıdaki gibidir:

Afin fonksiyon birinci dereceden bir polinom fonksiyonudur, yani grafikte gösterilen düz bir çizgi olan bir fonksiyondur. İlgili işlevler aşağıdaki gibidir:

$f(x)=mx+n$

Altın

$m$

çizginin eğimi ve

$n$

Bu y-kesme noktasıdır, yani fonksiyonun dikey eksenle kesiştiği yerdir.

Matematikte afin fonksiyonlara doğrusal cebir bağlamında doğrusal dönüşümler de denir.

Doğrusal bir fonksiyon, bağımsız bir terimi olmayan bir afin fonksiyondur. Bu nedenle doğrusal fonksiyonların formülü şöyledir:

$f(x)=mx$

Altın

$m$

doğrunun eğimidir.

Doğrusal fonksiyonun ve afin fonksiyonun etki alanı ve aralığı (veya aralığı) tamamı gerçek sayılardır:

$\text{Dom } f=\mathbff{R}$

$\text{Im } f= \mathbb{R}$

Doğrusal bir fonksiyon ile afin fonksiyon arasındaki fark nedir?

Artık doğrusal fonksiyon ve afin fonksiyon kavramlarını gördüğünüze göre birbirlerine çok benzediklerini fark etmişsinizdir. Ancak aralarındaki şu fark çok önemlidir:

Doğrusal fonksiyon ile afin fonksiyon arasındaki tek fark, doğrusal fonksiyonun bağımsız bir terimi olmaması, afin fonksiyonun ise kesme katsayısının (n) her zaman sıfırdan (0) farklı olmasıdır.

Doğrusal fonksiyon

$f(x)=mx$

doğrusal fonksiyon

$f(x)=mx+n$

Bu , doğrusal bir fonksiyonun her zaman koordinat orijini olan (0,0) noktasından geçtiği anlamına gelir. Öte yandan, bir afin fonksiyonun kesme noktası 0’dan farklı olduğundan hiçbir zaman bu noktadan geçmeyecektir.

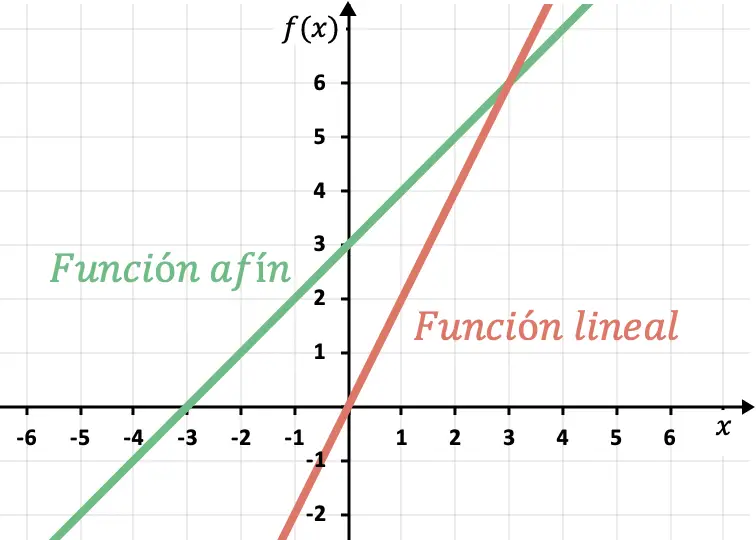
Doğrusal bir fonksiyon ile afin fonksiyon arasındaki fark nedir?

Doğrusal veya afin bir fonksiyonun eğimi ve y kesme noktası

Bu bölümde terimlerin anlamını anlamak için afin veya doğrusal fonksiyon örneğini analiz edeceğiz.

$m$

$n$

veya başka bir deyişle eğim ve y-kesişim noktası.

Grafikte gösterilen fonksiyonun ifadesini belirleyin ve onu doğrusal veya afin fonksiyon olarak sınıflandırın.

Bu tür işlevler aşağıdaki ifadeyi takip eder:

$f(x)=mx+n$

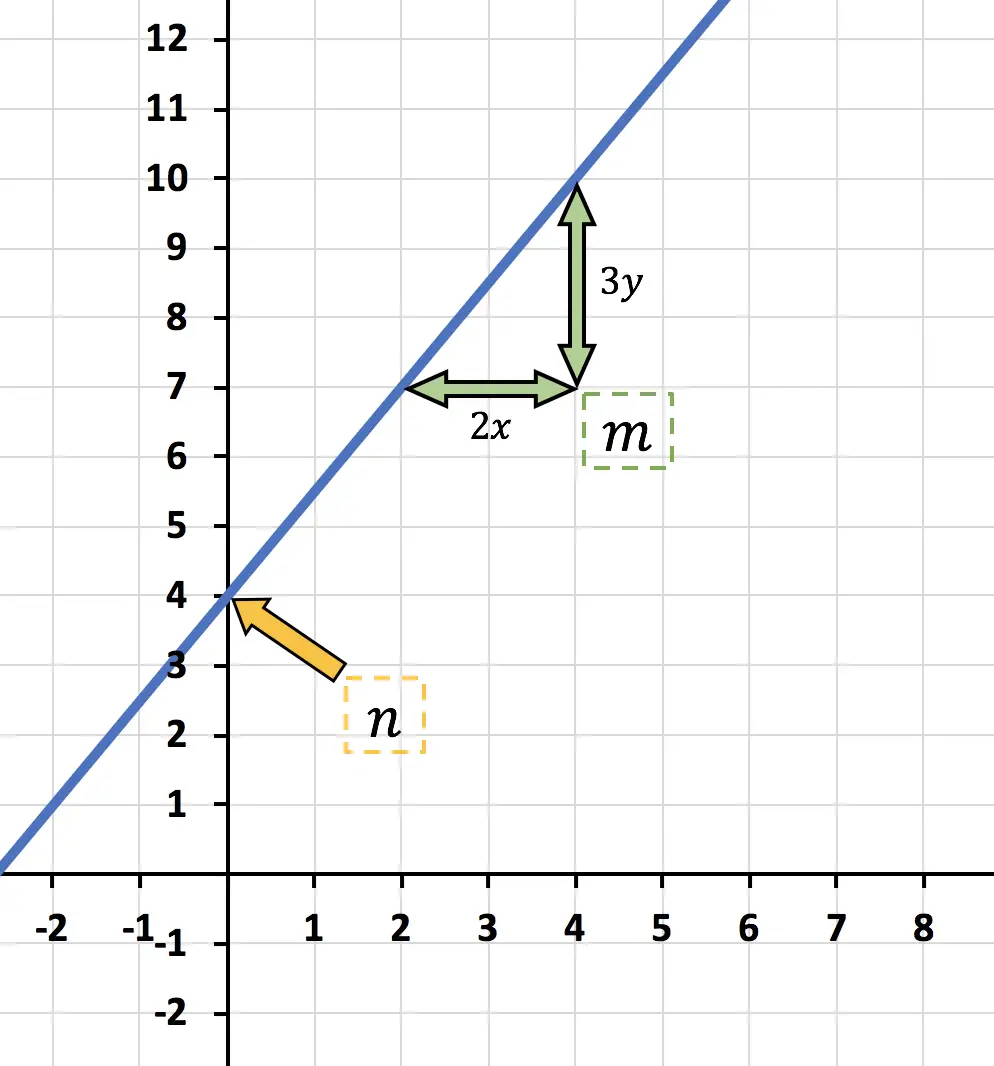
eğim ve y-kesişim noktası doğrusal veya afin fonksiyon m ve n anlamına gelir

$n$

Bu, y kesme noktasıdır, yani fonksiyonun dikey Y ekseniyle kesiştiği yerdir. Yani bu durumda:

$n=4$

Diğer tarafta,

$m$

doğrunun eğimidir. Y, iki nokta arasındaki y farkını aynı iki nokta arasındaki x farkına bölerek hesaplanabilir:

$m=\cfrac{\Delta y }{\Delta x} = \cfrac{3}{2}$

$m$

“her x için y ne kadar artar” diyor, yani bu durumda “her 2x için 3y artar” fonksiyonu.

Sonuç olarak grafikte temsil edilen afin fonksiyonun ifadesi şu şekildedir:

$\displaystyle \bm{f(x)=}\frac{\bm{3}}{\bm{2}}\bm{x+4}$

Ek olarak, y kesme noktası sıfır olmadığı için bu bir afin fonksiyondur .

Anlayışınızı tamamlamak için aşağıda size daha fazla doğrusal ve afin fonksiyon örneği gösteriyoruz:

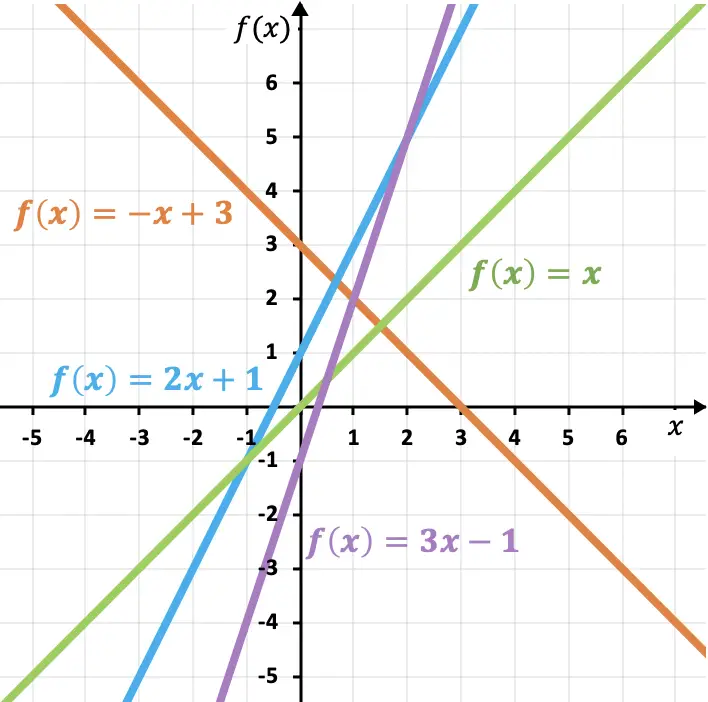
Bu örneklerde görebileceğiniz gibi eğim ne kadar büyük olursa çizgi de o kadar dik olur ve dolayısıyla fonksiyon da o kadar büyük olur. Benzer şekilde eğim katsayısı da bir fonksiyonun büyümesini veya azalmasını belirler:

Eğim pozitifse fonksiyon artıyor demektir, yani x arttıkça artar.
Eğim negatifse fonksiyon azalıyor demektir, yani x arttıkça azalır.

Ek olarak, iki çizginin paralel mi yoksa dik mi olduğunu eğimlerinden de anlayabilirsiniz:

Eğimi aynı olan iki doğru paraleldir yani hiçbir noktada kesişmezler veya tamamen aynıdırlar.

$m_1 = m_2$

Öte yandan, iki çizgi diktir , yani eğimleri aşağıdaki ilişkiye karşılık geliyorsa dikey bir açıyla (90°) kesişirler:

$m_1 = -\cfrac{1}{m_2}$

Afin veya doğrusal bir fonksiyonun temsiline örnek

Bir örnek kullanarak birinci dereceden bir fonksiyonun grafiğinin nasıl çizileceğini görelim.

Aşağıdaki afin fonksiyonun grafiğini çizin:

$f(x)=2x-1$

Yapmamız gereken ilk şey bir değer dizisi oluşturmaktır. Bunun için istediğimiz değerleri veriyoruz

$x$

değerlerini elde etmek

$f(x)$

$f(x)=2x-1$

$x= 0 \ \longrightarrow \ f(0) = 2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1) = 2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2) = 2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3) = 2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4) = 2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

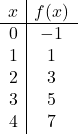
İki noktalı bir değerler tablosu yeterli olsa da doğru olduğundan emin olmak için daha fazla nokta yapabiliriz.

Değer tablosunu oluşturduktan sonra grafikteki noktaları çizeriz:

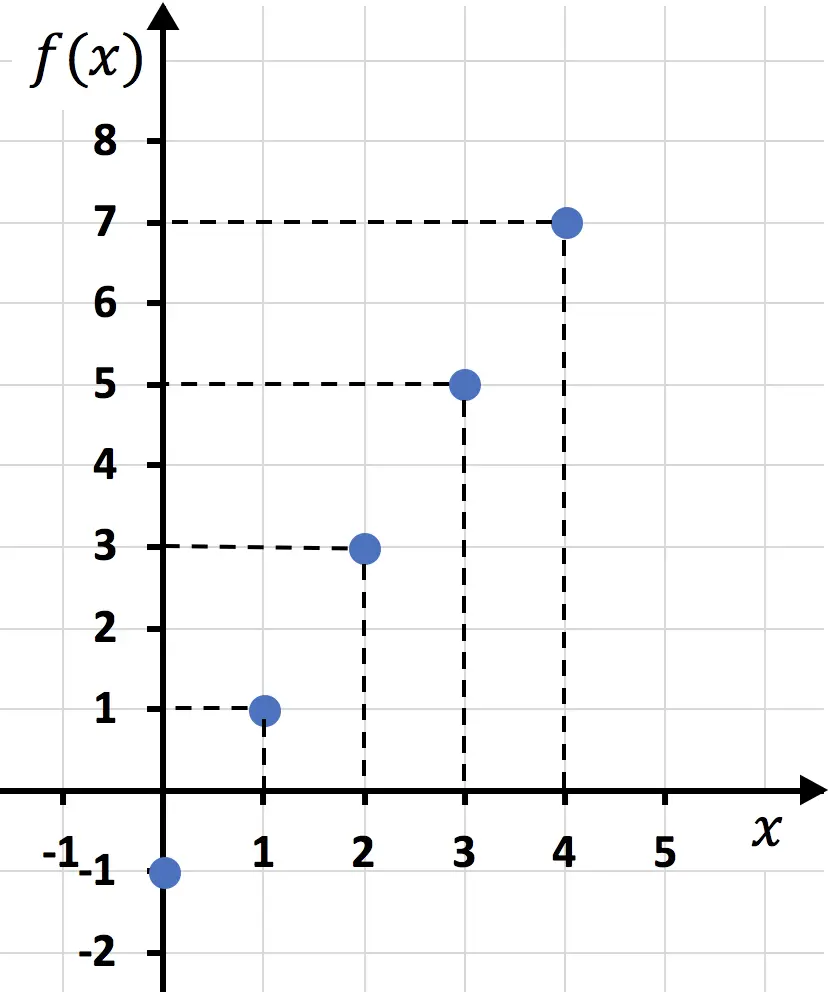
bir çizginin veya doğrusal bir fonksiyonun veya ve afin nasıl temsil edileceği

Son olarak noktaları birleştirip bir çizgi çiziyoruz:

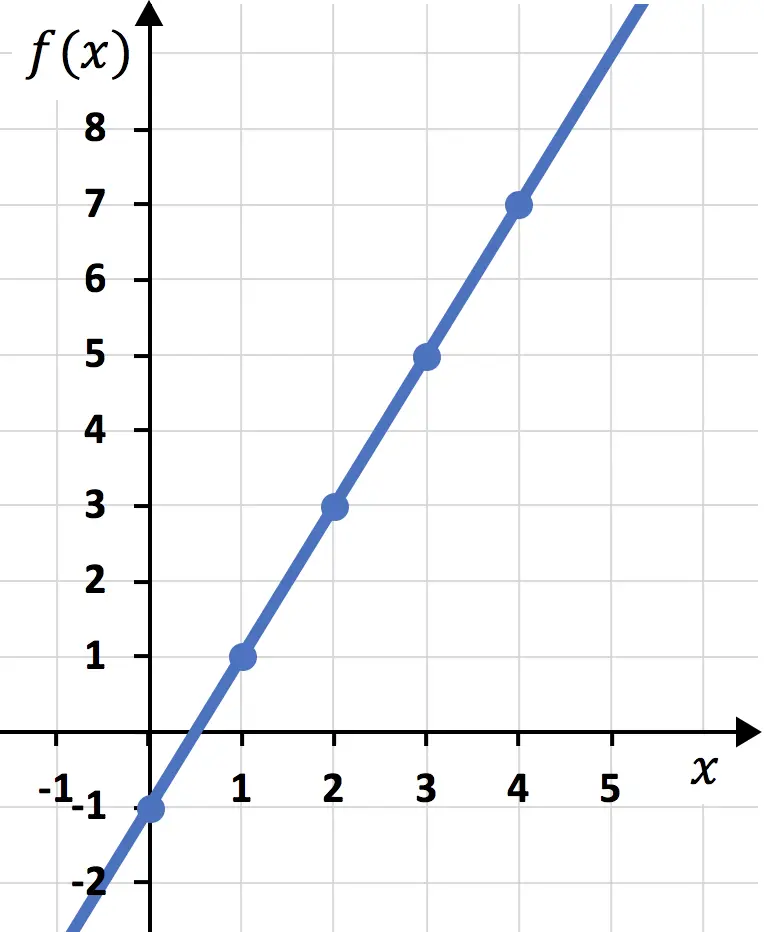
doğrusal veya afin fonksiyonun grafiksel gösterimi

Ve bu şekilde fonksiyonu zaten bir grafik üzerinde göstermiş olduk. Gördüğünüz gibi karmaşık değil, sadece önce bir değerler tablosu hazırlamanız, ardından noktaları bir grafik üzerine çizmeniz gerekiyor.

İki noktadan doğrusal veya afin fonksiyon nasıl hesaplanır

Şimdi bir örnek kullanarak iki noktadan doğrusal veya afin fonksiyonun nasıl bulunacağını görelim:

Aşağıdaki koşulları karşılayan doğrusal fonksiyonu hesaplayın
$f(3)=5$

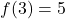
ve noktadan geç

$(1,-1).$

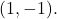
Öncelikle,

$f(3)=5$

Bu, fonksiyonun noktadan geçtiği anlamına gelir

$(3,5)$

Dolayısıyla fonksiyonun geçtiği iki noktamız olduğundan eğimi hesaplayabiliriz.

$m$

işlev:

İki nokta göz önüne alındığında,

$P_1=(x_1,y_1)$

$P_2=(x_2,y_2)$

, eğim

$m$

fonksiyonun hesaplanması:

$m=\cfrac{y_2-y_1}{x_2-x_1}$

Bizim durumumuzda fonksiyon noktalardan geçiyor

$(3,5)$

$(1,-1)$

. Yani eğim

$m$

fonksiyonun anlamı:

$m=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{-1-5}{1-3} = \cfrac{-6}{-2} = 3$

Bu nedenle fonksiyon şu şekilde olacaktır:

$f(x) = mx+n \ \xrightarrow{m \ = \ 3} \ f(x)=3x+n$

Bir kez bildiğimizde

$m$

gizemi çözebiliriz

$n$

. Bunu yapmak için fonksiyona ait bir noktanın koordinatlarını denklemde yerine koyarız. Örneğin (3.5) numaralı nokta:

$f(x) = 3x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ 5} \ 5=3\cdot 3+n$

Ortaya çıkan denklemi çözüyoruz:

$5=3\cdot 3+n$

$5= 9 + n$

$5-9=n$

$-4=n$

Dolayısıyla doğrusal fonksiyon şu şekildedir:

$\bm{f(x)=3x-4}$

Doğrusal ve afin fonksiyonlarla ilgili çözülmüş alıştırmalar

1. Egzersiz

Aşağıdaki afin fonksiyonunun eğimini ve kökenini belirleyin:

$f(x)=-5x-2$

Çözümü görün

Doğrusal bir fonksiyon şu forma sahiptir:

$f(x)=mx+n .$

Dolayısıyla fonksiyonun eğimi x’e eşlik eden sayıdır ve bu durumda bu sayı -5’tir:

$\bm{m=-5}$

Ve y kesme noktası bağımsız terimdir, bu durumda bu -2’dir:

$\bm{n=-2}$

Alıştırma 2

Aşağıdaki afin fonksiyonun grafiğini çizin:

$f(x)=x+1$

Çözümü görün

İlk önce değerleri veriyoruz

$x$

değerler tablosunu oluşturmak için:

$x= 0 \ \longrightarrow \ f(0)=0+1 = 1$

$x= 1 \ \longrightarrow \ f(1)=1+1= 2$

$x= 2 \ \longrightarrow \ f(2)=2+1 = 3$

$x= 3 \ \longrightarrow \ f(3)=3+1 = 4$

$x= 4 \ \longrightarrow \ f(4)=4+1 = 5$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 1 \\ 1 & 2 \\ 2 & 3 \\ 3 & 4 \\ 4 & 5 \end{array}$

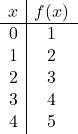
Daha sonra değerler tablosundaki noktaları grafikte temsil edip çizgiyi çiziyoruz:

Alıştırma 3

Aşağıdaki afin fonksiyonunu grafik üzerinde çizin:

$f(x)=-2x+6$

Çözümü görün

İlk önce değerleri veriyoruz

$x$

değerler tablosunu oluşturmak için:

$x= 0 \ \longrightarrow \ f(0)=-2\cdot0+6=6$

$x= 1 \ \longrightarrow \ f(1)=-2\cdot1+6=4$

$x= 2 \ \longrightarrow \ f(2)=-2\cdot2+6=2$

$x= 3 \ \longrightarrow \ f(3)=-2\cdot3+6=0$

$x= 4 \ \longrightarrow \ f(4)=-2\cdot4+6=-2$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & 6 \\ 1 & 4 \\ 2 & 2 \\ 3 & 0 \\ 4 & -2 \end{array}$

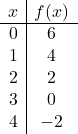
Ve son olarak değerler tablosundaki noktaları grafik üzerinde temsil ediyoruz ve çizgiyi çiziyoruz:

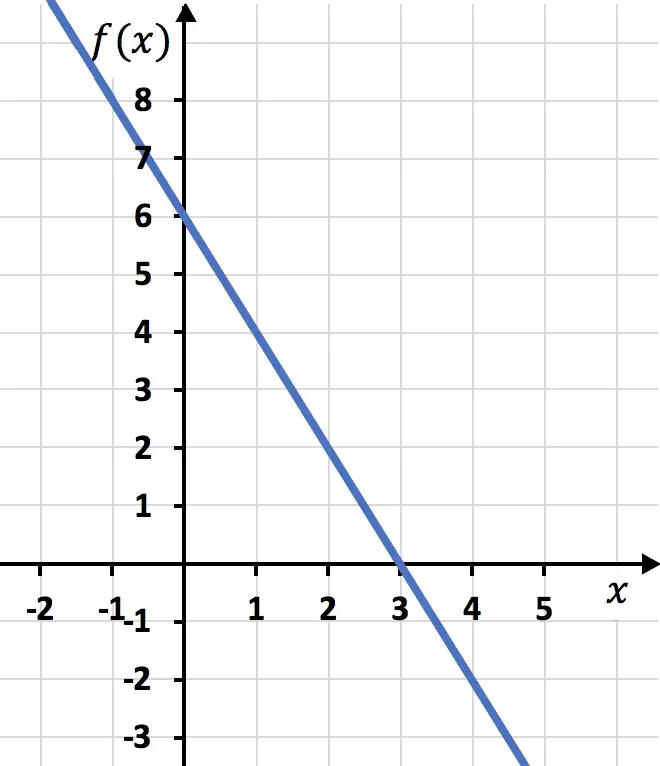
Doğrusal ve afin fonksiyonun adım adım çözüldüğü egzersiz

Alıştırma 4

(2,3) ve (0,1) noktalarından geçen afin fonksiyonunun ifadesini bulun.

Çözümü görün

Fonksiyon (2,3) ve (0,1) noktalarından geçtiğine göre fonksiyonun eğimi:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{1-3}{0-2} = \cfrac{-2}{-2} = 1$

Ve fonksiyon şu şekilde olacaktır:

$f(x)=mx+n \ \xrightarrow{m \ = \ 1} \ f(x)=1x+n$

m’yi bildiğimizde n’yi hesaplayabiliriz. Bunun için fonksiyona ait bir noktanın koordinatlarını denklemde yerine koymamız gerekir. Örneğin (2,3) noktası:

$f(x)=x+n \ \xrightarrow{x \ = \ 2 \ ; \ f(x) \ = \ 3}$

$3=2+n$

Şimdi ortaya çıkan denklemi çözmeliyiz:

$3-2=n$

$1 = n$

Dolayısıyla fonksiyon aşağıdaki ifadeye karşılık gelir:

$\bm{f(x)=x+1}$

Alıştırma 5

Aşağıdaki afin fonksiyonun grafiğini çizin:

$f(x)=2x-1$

Çözümü görün

İlk önce değerleri veriyoruz

$x$

değerler tablosunu oluşturmak için:

$x= 0 \ \longrightarrow \ f(0)=2\cdot0-1=-1$

$x= 1 \ \longrightarrow \ f(1)=2\cdot1-1=1$

$x= 2 \ \longrightarrow \ f(2)=2\cdot2-1=3$

$x= 3 \ \longrightarrow \ f(3)=2\cdot3-1=5$

$x= 4 \ \longrightarrow \ f(4)=2\cdot4-1=7$

$\begin{array}{c|c} x & f(x) \\ \hline 0 & -1 \\ 1 & 1 \\ 2 & 3 \\ 3 & 5 \\ 4 & 7 \end{array}$

Daha sonra değerler tablosundaki noktaları grafikte temsil edip çizgiyi çiziyoruz:

Doğrusal veya afin fonksiyonun grafiğini çizmek için çözülmüş alıştırmalar

Alıştırma 6

Aşağıdaki iki koşulu karşılayan doğrusal fonksiyonu hesaplayın:

$\begin{array}{c}f(3) =-2 \\[3ex] f(-1)=6 \end{array}$

Çözümü görün

Gerçekleşsin

$f(3)=-2$

Bu, fonksiyonun (3,-2) noktasından geçtiği anlamına gelir. Ve aynı şekilde,

$f(-1)=6$

Bu, fonksiyonun (-1,6) noktasından geçtiği anlamına gelir.

Yani fonksiyon (3,-2) ve (-1,6) noktalarından geçer, dolayısıyla eğimi:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{6-(-2)}{-1-3} = \cfrac{8}{-4} = -2$

Bu nedenle fonksiyon şu şekilde olacaktır:

$f(x)=mx+n \ \xrightarrow{m \ = \ -2} \ f(x)=-2x+n$

Ve m’yi bildiğimizde n’yi hesaplayabiliriz. Bunu yapmak için fonksiyona ait bir noktanın koordinatlarını denklemde yerine koyarız. Örneğin (3,-2) noktası:

$f(x)=-2x+n \ \xrightarrow{x \ = \ 3 \ ; \ f(x) \ = \ -2} \ -2=-2(3)+n$

Ve ortaya çıkan denklemi çözüyoruz:

$-2=-6+n$

$-2+6=n$

$4 = n$

Bu nedenle fonksiyon şu şekildedir:

$\bm{f(x)=-2x+4}$

Egzersiz 7

Gerçekleştirdiği afin işlevi bulun

$f(1) =6$

(3.5) noktasından geçer.

Çözümü görün

Gerçekleşsin

$f(1)=6$

Bu, fonksiyonun (1,6) noktasından geçtiği anlamına gelir.

Dolayısıyla fonksiyon (1.6) ve (3.5) noktalarından geçer ve dolayısıyla eğimi:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{5-6}{3-1} = \cfrac{-1}{2} = -\cfrac{1}{2}$

Bu nedenle fonksiyon şu şekilde olacaktır:

$\displaystyle f(x)=mx+n \ \xrightarrow{m \ = \ -\frac{1}{2}} \ f(x)=-\frac{1}{2}x+n$

M terimini bildiğimizde n katsayısını hesaplayabiliriz. Bunu yapmak için fonksiyona ait bir noktanın koordinatlarını denklemde yerine koyarız. Örneğin (1,6) noktası:

$\displaystyle f(x)=-\frac{1}{2}x+n \ \xrightarrow{x \ = \ 1 \ ; \ f(x) \ = \ 6} \ 6=-\frac{1}{2}\cdot 1+n$

Ortaya çıkan denklemi çözüyoruz:

$6=-\cfrac{1}{2}+n$

$6+\cfrac{1}{2}=n$

Kesirleri eklemek için önce bunları ortak bir paydaya indirgemeniz, ardından payları eklemeniz gerektiğini unutmayın:

$\cfrac{2 \cdot 6}{2} +\cfrac{1 \cdot 1}{2}=n$

$\cfrac{12}{2} +\cfrac{1}{2}=n$

$\cfrac{13}{2}=n$

Bu nedenle fonksiyon şu şekildedir:

$\displaystyle \bm{f(x)=-}\mathbf{\frac{1}{2}}\bm{x +}\mathbf{\frac{13}{2}}$

Egzersiz 8

Doğrusal ve afin fonksiyonlarla ilgili aşağıdaki problemi çözün:

Bir mağaza bir üründen birim fiyatı 15€ olduğunda 40 adet, birim fiyatı 10€ olduğunda 65 adet satmaktadır.

Afin fonksiyon olduğunu varsayarak ürünün talep fonksiyonunu hesaplayın.
Fiyat 12 €/adet olarak belirlenirse kaç adet satılacaktır?

Çözümü görün

Bir afin fonksiyon olduğu için fonksiyon şu türden olacaktır:

$f(x)=mx+n .$

Altın

$x$

ürünün birim fiyatı olacak ve

$f(x)$

satılan birimler olacak.

Basın bülteninde birim fiyatı 15€ olduğunda 40 adet satıldığı belirtiliyor. Bu nedenle,

$x$

fiyat ve

$f(x)$

satılan birimlerde aşağıdaki eşitliğe uyulmalıdır:

$f(15)=40$

Fiyatı 10€/adet olduğunda ise 65 adet satılıyor. Yani aynı mantığı kullanarak:

$f(10)=65$

Gerçekleşsin

$f(15)=40$

Bu, fonksiyonun (15.40) noktasından geçtiği anlamına gelir. VE

$f(10)=65$

Bu, fonksiyonun (10.65) noktasından geçtiği anlamına gelir.

Dolayısıyla fonksiyonun eğimi şu şekildedir:

$m=\cfrac{y_2-y_1}{x_2-x_1}= \cfrac{65-40}{10-15} = \cfrac{25}{-5} = -5$

Bu nedenle fonksiyon şu şekilde olacaktır:

$f(x)=mx+n \ \xrightarrow{m \ = \ -5} \ f(x)=-5x+n$

m’yi bildiğimizde n’yi hesaplayabiliriz. Bunu yapmak için fonksiyona ait bir noktanın koordinatlarını denklemde yerine koyarız. Örneğin şu nokta (15:40):

$f(x)=-5x+n \ \xrightarrow{x \ = \ 15 \ ; \ f(x) \ = \ 40} \ 40=-5\cdot 15+n$