Doğrusal regresyon , iki sürekli değişken arasındaki ilişkiyi incelemek için kullanılan istatistiksel bir yöntemdir. Doğrusal regresyonun ana fikri verilere en iyi uyan düz çizgiyi bulmaktır. Ayrıca bir değişkenin değerini diğerinin değerine göre tahmin etmenize olanak tanır.
Bu düz çizgiye “regresyon” denir ve bilinmeyen değerleri tahmin etmek veya değişkenler arasındaki ilişkiyi anlamak için kullanılır. Özetle doğrusal regresyon, iki sürekli değişken arasındaki ilişkiyi analiz etmek ve modellemek için kullanılan bir araçtır.
Doğrusal regresyon neden önemlidir?
Doğrusal regresyon önemlidir çünkü iki sürekli değişken arasındaki ilişkiyi modellemenize ve analiz etmenize olanak tanır; bu, gelecekteki değerleri tahmin etmede ve verilerdeki kalıpları ve eğilimleri belirlemede yararlı olabilir.
Ek olarak, doğrusal regresyon istatistiklerde ve diğerlerinin yanı sıra ekonomi, psikoloji, tıp, mühendislik ve fizik dahil olmak üzere bilimsel ve sosyal araştırmaların çoğu alanında temel bir araçtır. Aynı zamanda endüstride ve iş dünyasında ticari karar vermede ve süreç optimizasyonunda da kullanılır.
Özetle, doğrusal regresyon, çeşitli araştırma ve uygulama alanlarındaki verilerin ve değişkenler arasındaki ilişkilerin analiz edilmesine ve daha iyi anlaşılmasına olanak tanıyan güçlü ve çok yönlü bir araçtır .
Doğrusal regresyon türleri nelerdir?
Doğrusal regresyonun çeşitli türleri vardır; bunlardan bazıları şunlardır:
basit doğrusal regresyon
Basit doğrusal regresyon analizi , bağımsız bir değişkenin, aralarında doğrusal bir ilişki olduğu düşünülen tek bir bağımlı değişken üzerindeki etkisini incelemek için yaygın olarak kullanılan bir araçtır. Basit doğrusal regresyon denklemi, bağımsız değişkenin değerlerine dayanarak bağımlı değişkenin değerlerini tahmin etmemizi sağlar.
Basit doğrusal regresyon formülü şöyledir:
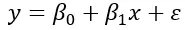
Burada β 0 , bağımsız değişken sıfır olduğunda bağımlı değişkenin değeridir. β 1, bağımsız değişkendeki birim değişiklik başına bağımlı değişkendeki değişikliği temsil eder ve ε, artık veya hatayı temsil eder. Yani verilerin, formülün doğrusal ilişkisiyle açıklanamayan değişkenliği.
Çoklu doğrusal gerileme
Çoklu doğrusal regresyon, incelenen bağımlı değişkeni etkileyebilecek birden fazla bağımsız değişkenin olduğu durumlarda kullanılır.
Çoklu doğrusal regresyonun formülü şöyledir:
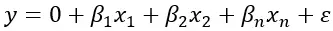
Y’nin bağımlı değişkeni temsil ettiği yerde , β 1 , β 2 , βn , Y’nin değerini etkileyebilecek bağımsız değişkenlerdir, regresyondur ve ε olası mevcut hatayı temsil eder. Bu formül, bağımsız değişkenlerin değerlerine dayanarak Y’nin değerini tahmin etmemizi sağlar.
Doğrusal regresyon formülü nedir?
Doğrusal regresyon formülü şöyledir:
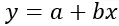
Altın:
y tahmin edilecek bağımlı değişkendir (veya yanıttır)
x, tahmini yapmak için kullanılan bağımsız (veya öngörücü) değişkendir
a kesişme noktasıdır (veya x=0 olduğunda regresyon çizgisinin Y ekseniyle kesiştiği noktadır)
b, regresyon çizgisinin eğimidir (x’in her değişimi için y’nin değişim oranını gösterir)
A ve b değerlerini bulmak için, gözlemlenen değerler ile regresyon çizgisinin öngördüğü değerler arasındaki karesel hataların toplamını en aza indirmeyi amaçlayan en küçük kareler yöntemini kullanıyoruz.
İşte formüller:
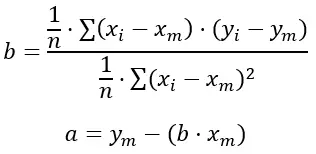
Altın:
n, sahip olduğumuz toplam veri kümesi sayısıdır.
x i ve y i toplamda aldığımız değerlerdir.
x m ve y m her değişkenin ortalama değerleridir.
Doğrusal regresyon yöntemi nasıl uygulanır?
Doğrusal regresyon yöntemi aşağıdaki adımlar izlenerek uygulanabilir:
- Veri toplayın : Yapılacak ilk şey sizi ilgilendiren verileri toplamaktır . Örneğin, bir grup insanın maaşı ile yaşı arasındaki ilişkiyi incelemek istiyorsanız, her birinin maaşı ve yaşı hakkında bilgi toplamanız gerekir.
- Verileri çizin – Daha sonra, bağımsız değişkenin (bu durumda yaş) yatay eksene ve bağımlı değişkenin (maaş) dikey eksene yerleştirildiği Kartezyen düzlemde verileri çizmeniz gerekir.
- Regresyon Doğrusunu Belirleyin : Verilere en iyi uyan regresyon çizgisi belirlenmelidir. Bu çizgi, örnek istatistiksel veriler kullanılarak hesaplanan doğrusal regresyon formülünden elde edilir.
- Uyum İyiliğini Değerlendirin – Regresyon çizgisinin verilere ne kadar iyi uyduğunu değerlendirmek önemlidir. Bu istatistiksel ölçümler kullanılarak yapılabilir.
- Tahminlerde bulunun – Son olarak, ortaya çıkan regresyon çizgisi kullanılarak tahminler yapılabilir. Örneğin, 30 yaşındaki bir kişinin maaşını tahmin etmek istiyorsanız doğrusal regresyon formülünü kullanır ve bunun yerine yaş değerini koyarsınız.
Bu adımların, kullanılan doğrusal regresyonun türüne ve kullanılan istatistiksel yazılıma bağlı olarak biraz değişebileceğini unutmamak önemlidir.
Doğrusal regresyon ne için kullanılır?
Bir değişkenin başka bir değişkenin değerini etkileyebildiği iki değişken arasındaki ilişkiyi analiz etmek istediğinizde doğrusal regresyon kullanılır. Bu nedenle, bağımsız bir değişkenin bağımlı değişkeni nasıl etkilediğini anlamak ve bağımlı değişkenin değerini bağımsız değişkene göre tahmin etmek için doğrusal regresyon kullanılabilir.
Doğrusal regresyonun iki değişken arasındaki ilişkinin doğrusal olduğunu varsaydığını , yani bağımlı değişkendeki değişimin bağımsız değişkendeki değişimle orantılı olduğunu varsaydığını belirtmek önemlidir.
Bu nedenle iki değişken arasında doğrusal bir ilişkiden şüphelenildiğinde doğrusal regresyon kullanılmalıdır. Bu koşulun sağlanamaması durumunda diğer doğrusal olmayan regresyon modellerinin veya farklı istatistiksel yöntemlerin kullanılması daha uygun olabilir.
Doğrusal regresyonun uygulamaları nelerdir?
Doğrusal regresyon diğerlerinin yanı sıra istatistik, ekonomi, mühendislik, sosyal bilimler, biyoloji gibi alanlarda çok çeşitli uygulamalarda kullanılır. Doğrusal regresyonun en yaygın uygulamalarından bazıları şunlardır:
- Trend Analizi – Geçmiş verilerdeki trendleri analiz etmek ve gelecekteki trendleri tahmin etmek.
- Tahmin – Bir veya daha fazla değişkenin geçmiş değerlerine dayanarak bir değişkenin gelecekteki değerini tahmin etmek.
- Pazar araştırması : Bir ürüne olan talep ile fiyatı arasındaki ilişkinin incelenmesi.
- Finansal Analiz – Bir şirketin gelirleri ve giderleri arasındaki ilişkiyi incelemek ve gelecekteki finansal sonuçları tahmin etmek.
- Epidemiyolojik çalışmalar : Bir risk faktörüne maruz kalma ile bir hastalığa yakalanma olasılığı arasındaki ilişkiyi incelemek.
- Sosyal Bilimler – Psikoloji, sosyoloji ve siyaset bilimi gibi alanlarda iki veya daha fazla değişken arasındaki ilişkiyi incelemek.
- Yöneylem Araştırması – Doğrusal regresyon, endüstri mühendisliği ve lojistik gibi alanlardaki karmaşık sistemleri modellemek ve optimize etmek için kullanılır.
- Çevre Bilimleri – Çevresel faktörler ile ekosistemler üzerindeki etkiler arasındaki ilişkiyi incelemek için kullanılır.
Doğrusal regresyonda artıklar nelerdir?
Doğrusal regresyonda artıklar , bağımlı değişkenin gözlenen değerleri ile doğrusal regresyon modelinin tahmin ettiği değerler arasındaki farktır . Başka bir deyişle, gerçek veri noktaları ile regresyon çizgisi arasındaki dikey mesafedir.
Artıkların ardındaki fikir, eğer regresyon çizgisi verilere iyi uyuyorsa artıkların küçük ve rastgele olması gerektiğidir. Artıkların büyük olması veya belirli bir örüntüyü takip etmesi, değişkenler arasındaki ilişkinin doğrusal olmadığının veya doğrusal regresyon modelinin verilere uymadığının işareti olabilir.
Artıklar ayrıca doğrusal regresyon modelinin doğruluğunu değerlendirmek ve modelin kalitesini etkileyebilecek aykırı değerleri veya etkili veri noktalarını belirlemek için de kullanılır.
Birden fazla bağımlı değişkenle doğrusal regresyon çalıştırabilir miyim?
Doğrusal regresyonda bağımlı değişken her zaman tek bir değişkendir. Ancak birden fazla bağımsız değişkeniniz olabilir. Bu durumda çoklu doğrusal regresyondan bahsedebiliriz .
Çoklu doğrusal regresyonda amaç, birden fazla bağımsız değişkenin tek bir bağımlı değişken üzerindeki etkisini incelemektir.
Doğrusal regresyonda katsayıları nasıl yorumlayabilirim?
Doğrusal regresyonda katsayılar, regresyon çizgisinin eğimini ve kesişimini temsil eder. Eğim, bağımsız değişkendeki birim değişim başına bağımlı değişkendeki değişimi gösterirken, kesişme noktası, bağımsız değişken sıfıra eşit olduğunda bağımlı değişkenin değerini temsil eder.
Doğrusal Regresyonun Sayısal Örnekleri
Basit bir örnek şu olabilir:
Bir grup insan için aşağıdaki yaş ve boy verilerine sahip olduğumuzu varsayalım:
| yaş) | Yükseklik (cm) |
| 25 | 170 |
| 30 | 175 |
| 35 | 180 |
| 40 | 185 |
| Dört beş | 190 |
Bu kişilerin yaşları ile boyları arasında bir ilişki olup olmadığını tespit etmek istiyoruz. Bunu yapmak için doğrusal regresyon kullanacağız.
Öncelikle verilerle istatistiksel bir grafik çizebiliriz (bu durumda dağılım grafiği kullanmanızı öneririz):
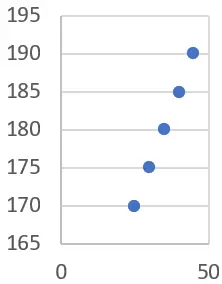
Yaş arttıkça boyun da arttığına dair net bir eğilim olduğunu görebiliyoruz. Bunu doğrusal regresyon çizgisini hesaplayarak doğrulayabiliriz.
Doğrusal regresyon çizgisinin katsayılarını daha önce gördüğümüz formüllerle hesaplayarak şunu elde ederiz:
= 145’te
b = 1
Bu nedenle doğrusal regresyon çizgisinin denklemi şöyledir:
Boy = 145 + 1 Yaş
Bir kişinin boyunu yaşına göre tahmin etmek için bu denklemi kullanabiliriz. Örneğin, bir kişi 32 yaşındaysa boyunun şu şekilde olacağını tahmin edebiliriz:
Yükseklik = 145 + 1 32 = 177 cm