Doğrusal bir fonksiyonun türevi

Bu yazıda size doğrusal bir fonksiyonun türevinin ne kadar olduğunu göstereceğiz. Ek olarak, doğrusal fonksiyonların türevlerinin birkaç örneğini çözüyoruz ve bu tür türevin formülünü gösteriyoruz. Hatta doğrusal fonksiyonların türevleri üzerine çözülmüş alıştırmalar bile bulacaksınız.

Doğrusal bir fonksiyonun türevi nedir?

Doğrusal bir fonksiyonun türevi birinci derece terimin katsayısıdır , yani f(x)=Ax+B doğrusal fonksiyonunun türevi A’ya eşittir.

$f(x)=Ax+B\quad\color{orange}\bm{\longrightarrow}\color{black}\quad f'(x)=A$

Bir sabitin türevi sıfır olduğundan bağımsız terim türevden çıkarılır. Birinci dereceden bir terimin türevi ise o terimin katsayısıdır. Dolayısıyla bu iki tip fonksiyonun toplamının türevi doğrusal terimin katsayısıdır.

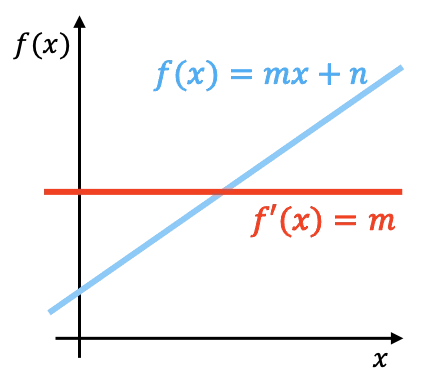
Geometrik olarak doğrusal bir fonksiyonun türevi o fonksiyonun eğimidir. Yukarıdaki grafikte türeviyle birlikte doğrusal bir fonksiyonun temsil edildiğini görebilirsiniz.

Doğrusal fonksiyonların türevlerine örnekler

Doğrusal bir fonksiyonun türevinin tanımı göz önüne alındığında, kavramı anlamayı tamamlamak için birkaç doğrusal fonksiyon örneği hesaplayacağız:

$\begin{array}{c}f(x)=3x+1\quad\longrightarrow\quad f'(x)=3\\[3ex]f(x)=5x-4\quad\longrightarrow\quad f'(x)=5\\[3ex] f(x)=-2x+9\quad\longrightarrow\quad f'(x)=-2\end{array}$

Doğrusal fonksiyonun türevinin, fonksiyonun bağımsız bir terimi olmadığında veya başka bir deyişle birinci dereceden yalnızca bir terime sahip olduğu durumlarda her zaman x değişkenine eşlik eden sayı olduğunu unutmayın. Örneğin:

$f(x)=8x\quad\longrightarrow\quad f'(x)=8$

Bu nedenle doğrusal bir fonksiyonun türevi, bağımsız değişkeni olmayan, basit bir sayı olan bir fonksiyondur.

Doğrusal bir fonksiyonun türevinin kanıtı

Daha sonra doğrusal bir fonksiyonun türevinin formülünü göstereceğiz.

f herhangi bir doğrusal fonksiyon olsun :

$f(x)=Ax+B$

Bir fonksiyonun bir noktadaki türevini hesaplama formülü şöyledir:

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}$

Dolayısıyla, doğrusal bir fonksiyon için önceki limiti hesaplarsak şunu elde ederiz:

$\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}=\frac{A(a+h)+B-(A\cdot a+B)}{h}$

Parantezleri çözüyoruz:

$\displaystyle f'(a)=\frac{Aa+Ah+B-Aa-B}{h}$

Payda çalışıyoruz:

$\displaystyle f'(a)=\frac{Ah}{h}$

Ve son olarak kesri sadeleştiriyoruz:

$\displaystyle f'(a)=A$

Sonuç olarak, doğrusal bir fonksiyonun türevi, herhangi bir noktadaki birinci derece terimin katsayısına eşittir. Böylece doğrusal bir fonksiyonun türevinin formülü türetilir.