Bu sayfada bir doğrunun eğiminin en detaylı açıklamasını bulacaksınız: formülü nedir, hesaplama örnekleri, bir doğrunun eğimi kavramı ne anlama gelir… Ayrıca eğimi nasıl kolayca tanımlayabileceğinizi de görebileceksiniz. Denkleminden bir doğruyu çıkaracak ve ayrıca adım adım çözülen alıştırmalarla pratik yapabileceksiniz.
Bir doğrunun eğimi formülü
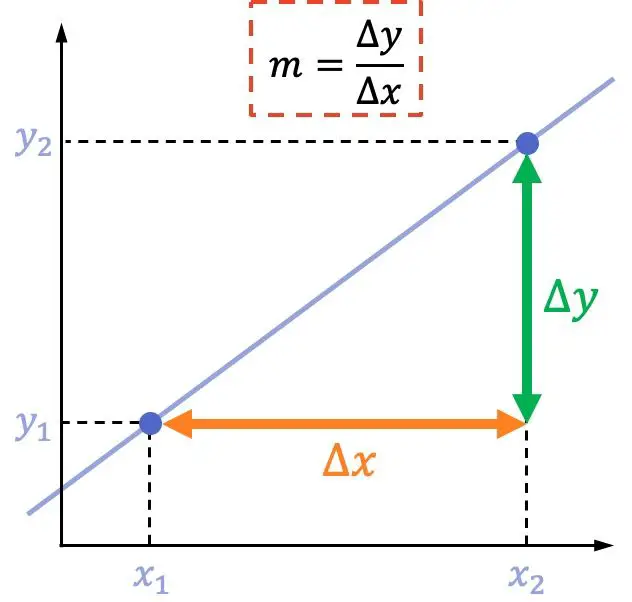
Bir doğrunun eğimi , iki nokta arasındaki dikey yer değiştirmenin bu aynı iki nokta arasındaki yatay yer değiştirmeye bölünmesine eşittir.
Yani bir doğru üzerinde iki nokta verildiğinde:
![]()
Bir doğrunun eğiminin formülü:
![]()
Bir doğrunun eğimini iki noktadan hesaplama örneği
Daha sonra bir doğrunun eğiminin aşağıdaki formülle nasıl hesaplandığına dair bir örnek göreceğiz:
- Aşağıdaki iki noktadan geçen doğrunun eğimini hesaplayınız:
![]()
Bu doğrunun eğimini bulmak için formülü uygulamanız yeterlidir:
![]()
Bu nedenle doğrunun eğimi 3’e eşittir.
Bir doğrunun eğimini denkleminden bulma
Yukarıdaki bölümde bir doğrunun eğiminin sayısal olarak nasıl belirleneceğini gördük. Ancak her zaman hesaplama yapmak gerekli değildir ancak değeri bir doğrunun denkleminden de belirlenebilir. Her denklem türü farklıdır, bu nedenle her durumu ayrı ayrı analiz edeceğiz.
Doğrunun açık denklemi verilen eğim
Doğrunun açık denklemi aşağıdaki ifadeyi takip eder:
![]()
Daha sonra parametre
![]()
doğrunun eğimine karşılık gelir.
Doğrunun nokta-eğim denklemi verilen eğim
Doğrunun nokta-eğim denkleminin formülü aşağıdaki gibidir:
![]()
Daha önce olduğu gibi, katsayı
![]()
doğrunun eğimine karşılık gelir.
Doğrunun örtülü denklemi verilen eğim
Doğrunun örtülü denklemi göz önüne alındığında (genel veya Kartezyen denklem olarak da bilinir):
![]()
Doğrunun eğimi şu şekilde bulunabilir:
![]()
Çizginin yön vektörünü dikkate alan eğim
Doğrunun yön vektörü, onun yönünü gösteren vektördür. Yani, eğer bir doğrunun yön vektörü:
![]()
Bu doğrunun eğimi:
![]()
bir açı verilen eğim
Son olarak, eğer bir çizgi bir açı oluşturuyorsa
![]()
apsis ekseninin (X ekseni) pozitif kısmında eğimi açının tanjantına eşdeğerdir:
![]()
Bir doğrunun eğiminin anlamı
Yukarıdaki tüm bilgilerle bir çizginin eğimini nasıl bulacağımızı zaten gayet iyi biliyoruz. Ama gerçekte… bir çizginin eğimi ne anlama geliyor?
Bir çizginin eğimi, grafiğin her yatay birimi için çizginin yükseldiği dikey birimleri gösterir.
Örneğin aşağıdaki doğrunun gösteriminde eğimi 2’ye eşit olduğundan her yatay birim için 2 dikey birim ilerlediğini görebilirsiniz.

Ayrıca bir doğrunun eğimi de onun dikliğini gösterir:
- Bir doğru artıyorsa (yükseliyorsa) eğimi pozitiftir.
- Bir doğru azalıyorsa (alçalıyorsa) eğimi negatiftir.
- Bir doğru tamamen yatay ise eğimi 0’a eşittir.
- Bir doğru tamamen dik ise eğimi sonsuza eşittir.


Çizgilerin göreceli konumu
Öte yandan iki çizgi arasındaki göreceli konum eğimlerin özelliklerinden de bilinebilir:
- İki doğrunun eğimleri farklıysa bu onların kesiştiği , yani bir noktada kesiştiği anlamına gelir.
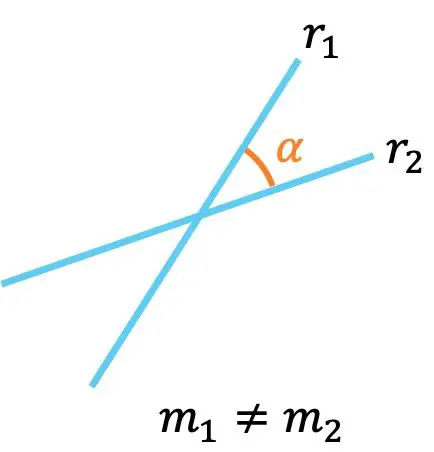
Ayrıca iki doğrunun eğimleri arasındaki açı da aşağıdaki formülle hesaplanabilir:
![]()
- İkincisi, eğer iki doğru aynı eğime sahipse, bu onların paralel olduğu anlamına gelir.

- Son olarak, iki dik veya dik çizginin (90° oluşturan) eğimleri aşağıdaki koşulu karşılar:

Bu, iki doğrunun birbirine paralel mi dik mi olduğunu bulmanın bir yoludur, ancak başka yöntemler de vardır ve bazıları daha hızlıdır. Daha fazlasını öğrenmek için çizgiler arasındaki diklik ve paralellik açıklamasına gidebilirsiniz. Ek olarak bu sayfalarda diğerine dik (veya paralel) bir doğrunun nasıl bulunacağı da açıklanmaktadır.
Bir çizginin eğimiyle ilgili çözülmüş problemler
1. Egzersiz
Aşağıdaki iki noktadan geçen doğrunun eğimini bulun:
![]()
Çizginin eğimini hesaplamak için aşağıdaki formülü kullanmanız gerekir:
![]()
Alıştırma 2
Aşağıdaki iki noktadan geçen doğrunun eğimini hesaplayınız:
![]()
Doğrunun eğimini bulmak için aşağıdaki formülü kullanmalısınız:
![]()
Alıştırma 3
Her çizginin eğimi nedir?
![Rendered by QuickLaTeX.com \begin{array}{lll} A) \ y= 2x+3 & \qquad & B) \ y-3=4(x+1) \\[2ex] C) \ 6x+2y-7=0 & \qquad & D) \ \begin{cases}x=3-t \\[2ex] y=1+2t \end{cases} \end{array}](https://mathority.org/wp-content/ql-cache/quicklatex.com-5d405c8176957af59906c98149714570_l3.png)
A) Doğru örtülü bir denklem olarak ifade edilir, yani eğimi 2’dir (eşlik eden terim)
![]()
).
B) Doğru, nokta-eğim denklemiyle tanımlanır, yani eğimi 4’tür (parantezlerden önceki sayı).
C) Doğru örtülü denklem formunda olduğundan eğimi:
![]()
D) Doğru, parametrik denklemler biçiminde tanımlanır, bu nedenle önce yön vektörünü bulmamız gerekir ve onunla çizginin eğimini hesaplayabiliriz. Dolayısıyla yön vektörünün bileşenleri katsayıya eşlik eden terimlerdir.
![]()
![]()
Doğrunun yön vektörünü bildiğimizde, doğrunun eğimini de belirleyebiliriz:
![]()
Alıştırma 4
Grafikle gösterilen her çizginin eğimini belirleyin:

mavi sağ
Mavi çizgi her X için bir Y artar, dolayısıyla eğimi 1’e eşittir.
![]()
sağ yeşil
Yeşil çizgi her X için üç Y artar, dolayısıyla eğimi 3’tür .
![]()
kırmızı cizgi
Kırmızı çizgi her X için iki Y azalır, dolayısıyla eğimi -2’ye eşittir .
![]()