Çapraz matris - Mathority

Bu sayfada köşegen matrisin ne olduğunu ve köşegen matris örneklerini göreceksiniz. Ayrıca bu tür matrislerle nasıl çalışılacağını, determinantlarının nasıl kolayca hesaplanacağını ve bunların nasıl ters çevrileceğini öğreneceksiniz. Ayrıca köşegen matrislerin özellikleri ve uygulamaları da vardır. Son olarak iki köşegenli matris ve üç köşegenli matrisin açıklamaları bulunmaktadır.

Köşegen matris nedir?

Köşegen matris, ana köşegen üzerinde olmayan tüm elemanların sıfır (0) olduğu bir kare matristir. Ana köşegenin elemanları sıfır olabilir veya olmayabilir.

Köşegen matrisin tam tanımını öğrendikten sonra köşegen matris örneklerini göreceğiz:

Köşegen matris örnekleri

2 × 2 boyutlu köşegen matris örneği

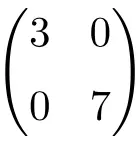
3×3 dereceli köşegen matris örneği

4×4 boyutunda köşegen matris örneği

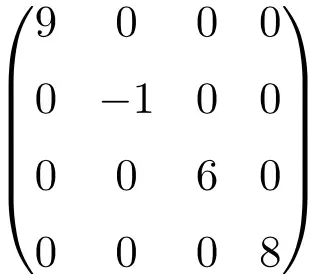
Bu tür matrisler genellikle köşegenin elemanlarını gösterecek şekilde yazılır:

$diag(2,5,1) = \left. \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Köşegen matrislerle işlemler

Köşegen matrislerin doğrusal cebir için bu kadar önemli olmasının nedenlerinden biri, hesaplamaları yapmanıza olanak sağlama kolaylığıdır. Matematikte bu kadar kullanılmalarının nedeni budur.

Köşegen matrisleri toplama ve çıkarma

İki köşegen matrisin toplanması (ve çıkarılması) çok basittir: yalnızca köşegenlerdeki sayıları ekleyin (veya çıkarın).

$\displaystyle \text{diag}(a_1,... ,a_n) \pm \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\pm b_1,..., a_n\pm b_n)$

Örneğin:

$\displaystyle \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} +\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & -4 \end{pmatrix} = \begin{pmatrix} 6& 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 2 \end{pmatrix}$

Çapraz matris çarpımı

İki köşegen matrisin çarpımını veya matris çarpımını çözmek için köşegenlerin elemanlarını birbiriyle çarpmanız yeterlidir.

$\displaystyle \text{diag}(a_1,... ,a_n) \cdot \text{diag}(b_1 ,... , b_n) = \text{diag}(a_1\cdot b_1,..., a_n\cdot b_n)$

Örneğin:

$\displaystyle \begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & -4 & 0 \\[1.1ex] 0 & 0 & -3 \end{pmatrix} \cdot\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & -2 & 0 \\[1.1ex] 0 & 0 & 6 \end{pmatrix} = \begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & -18 \end{pmatrix}$

Köşegen matrislerin gücü

Bir köşegen matrisin kuvvetini hesaplamak için köşegenin her elemanını üs değerine yükseltmemiz gerekir:

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle A^k= \text{diag}(a_1^k,... ,a_n^k)$

Örneğin:

$\displaystyle\left. \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix}\right.^3= \begin{pmatrix} 27 & 0 & 0 \\[1.1ex] 0 & 8 & 0 \\[1.1ex] 0 & 0 & 64 \end{pmatrix}$

Köşegen matrisin determinantı

Köşegen bir matrisin determinantı, ana köşegen üzerindeki elemanların çarpımıdır.

$\displaystyle A= \text{diag}(a_1,... ,a_n)$

$\displaystyle \text{det}(A)= \prod_{i =1}^n a_i$

Bir köşegen matrisin determinantını basitçe ana köşegeninin elemanlarını çarparak bulduğumuz aşağıdaki çözülmüş alıştırmaya bakın:

$\displaystyle \begin{vmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 3 \end{vmatrix} = 5 \cdot 2 \cdot 3 = 30$

Bu teoremin kanıtlanması kolaydır: köşegen matrisin determinantını bloklara (veya kofaktörlere) göre hesaplamanız yeterlidir. Bu gösterim aşağıda genel bir köşegen matris kullanılarak detaylandırılmıştır:

$\begin{aligned} \begin{vmatrix} a & 0 & 0 \\[1.1ex] 0 & b & 0 \\[1.1ex] 0 & 0 & c \end{vmatrix}& = a \cdot \begin{vmatrix} b & 0 \\[1.1ex] 0 & c \end{vmatrix} - 0 \cdot \begin{vmatrix} 0 & 0 \\[1.1ex] 0 & c \end{vmatrix} + 0 \cdot \begin{vmatrix} 0 & b \\[1.1ex] 0 & 0 \end{vmatrix} \\[2ex] & =a \cdot (b\cdot c) - 0 \cdot 0 + 0 \cdot 0 \\[2ex] & = a \cdot b \cdot c \end{aligned}$

Çapraz matrisi ters çevirme

Bir köşegen matris , ancak ve ancak ana köşegenin tüm elemanlarının 0’dan farklı olması durumunda tersinirdir . Bu durumda köşegen matrisin düzenli bir matris olduğunu söylüyoruz.

Ek olarak, bir köşegen matrisin tersi her zaman ana köşegenin tersi olan başka bir köşegen matris olacaktır:

$\displaystyle A= \begin{pmatrix} 3 & 0 & 0 \\[1.1ex] 0 & 2 & 0 \\[1.1ex] 0 & 0 & 8 \end{pmatrix} \ \longrightarrow \ A^{-1}=\begin{pmatrix} \frac{1}{3} & 0 & 0 \\[1.1ex] 0 & \frac{1}{2} & 0 \\[1.1ex] 0 & 0 & \frac{1}{8} \end{pmatrix}$

Önceki karakteristikten, bir köşegen matrisin tersinin determinantının, ana köşegenin terslerinin çarpımı olduğu sonucunu çıkarabiliriz:

$\displaystyle B= \begin{pmatrix} 2 & 0 & 0 \\[1.1ex] 0 & 4 & 0 \\[1.1ex] 0 & 0 & -1 \end{pmatrix}$

$\displaystyle\left| B^{-1}\right|=\cfrac{1}{2} \cdot \cfrac{1}{4} \cdot \cfrac{1}{-1}=-\cfrac{1}{8} = -0,125$

Köşegen matrislerin özellikleri

Herhangi bir köşegen matris aynı zamanda simetrik bir matristir .

Köşegen matris , hem üst hem de alt üçgen olan bir matristir .

Kimlik matrisi köşegen bir matristir:

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix}$

Benzer şekilde sıfır matrisi de köşegen bir matristir çünkü köşegen üzerinde olmayan tüm elemanları sıfırdır. Köşegendeki sayılar 0 olmasına rağmen.

$\begin{pmatrix} 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \\[1.1ex] 0 & 0 & 0 \end{pmatrix}$

Köşegen bir matrisin özdeğerleri (veya özdeğerleri), ana köşegeninin elemanlarıdır.

$\begin{pmatrix} 7 & 0 & 0 \\[1.1ex] 0 & 3 & 0 \\[1.1ex] 0 & 0 & 4 \end{pmatrix} \longrightarrow \ \lambda = 3 \ ; \ \lambda = 4 \ ; \ \lambda = 7$

Bir kare matris ancak ve ancak üçgensel ve normal ise köşegendir.

Bir köşegen matrisin eşleni başka bir köşegen matristir.

Köşegen Matris Uygulamaları

Gördüğümüz gibi köşegen matrislerle hesaplamaları çözmek çok basittir çünkü işlemlerde birçok sıfır yer alır. Bu nedenle matematik alanında oldukça faydalı olup yaygın olarak kullanılmaktadırlar.

Aynı nedenden dolayı, bir matrisin nasıl köşegenleştirileceği üzerine pek çok çalışma yapılmış ve aslında matrisleri köşegenleştirmeye yönelik bir yöntem bile geliştirilmiştir (karakteristik polinom kullanılarak).

Bu nedenle köşegenleştirilebilir matrisler de oldukça önemlidir. Bir matrisin ne zaman köşegenleştirilebileceği ve ne zaman köşegenleştirilemeyeceğine ilişkin koşulları belirleyen spektral ayrışma teoremi gibi.

iki köşeli matris

İki köşegenli bir matris, ana köşegende veya üst veya alt köşegende olmayan tüm elemanların 0 olduğu bir kare matristir.

Örneğin:

$\begin{pmatrix} 3 & 2 & 0 \\[1.1ex] 0 & -5 & 1 \\[1.1ex] 0 & 0 & 6 \end{pmatrix}$

üst iki köşeli matris

$\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 6 & 2 & 0 \\[1.1ex] 0 & 7 & 4 \end{pmatrix}$

alt iki köşeli matris

Ana köşegen ve birinci süper köşegen dolu olduğunda üst iki köşegenli matristen söz ederiz. Öte yandan, ana köşegen ve birinci alt köşegen dolu olduğunda, alt iki köşegenli bir matristen bahsediyoruz.

üç köşegen matris

Üç köşegenli bir matris, yalnızca sıfır olmayan elemanları ana köşegen ve üstündeki ve altındaki bitişik köşegenlerden oluşan bir kare matristir.

Örneğin:

$\begin{pmatrix} 2 & 3 & 0 & 0 \\[1.1ex] -4 & 5 & 9 & 0 \\[1.1ex] 0 & 1 & 6 & -2 \\[1.1ex] 0 & 0 & 8 & 7 \end{pmatrix}$

Dolayısıyla tüm köşegen, iki köşegen ve üç köşegen matrisler bant matrislerine örnektir. Çünkü bant matrisi, sıfır olmayan tüm elemanlarını ana köşegen etrafında bulunduran matristir.

Diyagonal matris

Köşegen matris nedir?

Köşegen matris örnekleri

Köşegen matrislerle işlemler

Köşegen matrisleri toplama ve çıkarma

Çapraz matris çarpımı

Köşegen matrislerin gücü

Köşegen matrisin determinantı

Çapraz matrisi ters çevirme

Köşegen matrislerin özellikleri

Köşegen Matris Uygulamaları

iki köşeli matris

üç köşegen matris

Yorum bırakın Yanıtı iptal et