Dik çizgiler (diklik) -

Bu sayfada dik çizgilerle ilgili her şeyi bulacaksınız: ne oldukları, iki doğru birbirine dik olduğunda, diğerine dik bir doğrunun nasıl hesaplanacağı, özellikleri,… Ayrıca örnekleri görebileceksiniz ve şunları yapabileceksiniz: Adım adım çözülen alıştırmalarla pratik yapın.

İki dik çizgi nedir?

Matematikte iki doğru, dört eşit dik açı (90°) oluşturan bir noktada kesiştiğinde diktir.

Ayrıca birbirine dik olan iki doğrunun yön vektörleri de dik olmalıdır.

İki çizginin dikliği genellikle sembolüyle gösterilir.

$\perp .$

Öte yandan, düzlemde iki doğru arasındaki göreceli konum kavramında 4 olasılığın bulunduğunu unutmayın: iki doğru kesen, dik, çakışık veya paralel olabilir. İsterseniz her çizgi tipinin anlamını sitemizden inceleyebilirsiniz.

İki çizginin dik olup olmadığını nasıl anlarsınız?

İki doğrunun dik olup olmadığını yön vektörlerinden veya eğimlerinden belirlemenin iki yolu vardır. Aşağıda her iki yöntemin de açıklaması bulunmaktadır, her ne kadar aynı amaca hizmet etseler de, her iki işlemin de nasıl yapılacağını bilmenizi öneririz çünkü her biri çizgilerin nasıl ifade edildiğine bağlıdır.

Çizgilerin yön vektörlerinden

İki çizginin ne zaman dik olduğunu bilmenin bir yolu, söz konusu çizgilerin yön vektörlerini kullanmaktır. Yön vektörünün bir çizginin yönünü gösteren vektör olduğunu unutmayın.

İki dik çizginin yön vektörleri de karşılıklı olarak diktir. Dolayısıyla iki doğrunun yön vektörlerinin nokta çarpımı 0’a eşitse bu doğruların dik olduğu anlamına gelir.

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s =0 \quad \longrightarrow \quad r \perp s$

Bir örnek kullanarak iki çizginin dikliğinin nasıl belirlendiğini görelim:

$\displaystyle r: \ \begin{cases} x=3-2t \\[2ex] y=6+3t \end{cases}\qquad \qquad s: \ \begin{cases} x=4+3t \\[2ex] y=-2+2t \end{cases}$

Her iki çizgi de parametrik denklemler olarak ifade edilir, dolayısıyla her satırın yön vektörünün bileşenleri parametrenin önündeki sayılardır.

$t:$

$\vv{\text{v}}_r =(-2,3) \qquad \qquad \vv{\text{v}}_s=(3,2)$

Her çizginin yön vektörünü öğrendikten sonra vektörler arasındaki çarpımı hesaplayarak çizgilerin dik olup olmadığını kontrol ederiz:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-2,3)\cdot (3,2) = -2\cdot 3 +3\cdot 2= \bm{0}$

İki vektörün nokta çarpımı sıfır olduğundan çizgiler diktir.

Çizgi eğimleri

İki çizginin dik olup olmadığını belirlemenin başka bir yolu da eğimlerini kullanmaktır. Bir doğrunun eğiminin katsayı olduğunu unutmayın

$m$

Bir doğrunun açık denklemi ve nokta-eğim denklemi.

$y=mx+n \qquad \qquad y-y_0=m(x-x_0)$

Ve bir doğrunun eğimi katsayılardan da elde edilebilir

$A$

$B$

bir doğrunun örtülü (veya genel) denkleminin:

$Ax+By+C= 0 \ \longrightarrow \ m = -\cfrac{A}{B}$

Böylece, iki dik çizginin eğimleri ters ve zıt işaretlidir, yani aşağıdaki eşitlik her zaman sağlanır:

$r \perp s \quad \longrightarrow \quad m_r=-\cfrac{1}{m_s}$

Yani iki farklı doğrunun eğimlerinin çarpımı -1’e eşitse bu, doğruların dik olduğu anlamına gelir:

$m_r\cdot m_s=-1\quad \longrightarrow \quad r \perp s$

Örneğin aşağıdaki iki çizgi birbirine diktir:

$r: \ y=2x+4 \qquad \qquad s: \ y=-\cfrac{1}{2} \ x-5$

Eğimlerinden birbirine dik iki doğru olduklarını gösterebiliriz. Her çizginin eğimi:

$m_r = 2 \quad \quad m_s=-\cfrac{1}{2}$

Şimdi eğimleri çarpıyoruz:

$\displaystyle 2 \cdot \left(-\frac{1}{2} \right) = -\cfrac{2}{2} = \bm{-1}$

İki eğim arasındaki çarpım -1’e eşittir, bu aslında birbirine dik iki doğru anlamına gelir.

Bir diğerine dik bir çizgi nasıl hesaplanır?

Her ne kadar yapılması zor gibi görünse de diğerine dik bir doğru bulmak oldukça basittir, bunun için sadece doğruya dik bir yön vektörüne ve doğruya ait bir noktaya ihtiyacınız vardır.

Tek zorluk, daha önce olduğu gibi, prosedürün çizgilerin ifade edildiği denklem türüne bağlı olmasıdır. Çünkü diğerine dik olan bir doğru yön vektörlerinden ya da eğimlerinden hesaplanabilir.

Sağdaki yön vektöründen

Verilen başka bir çizgiye dik olan bir çizgi, yön vektörü kullanılarak bulunabilir. Bunun nasıl yapıldığını bir örnekle görelim:

Çizgiye dik çizgiyi hesaplayın
$r$

noktadan geçen şey

$P(5,-1)$

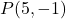
. düz olmak

$r:$

$\displaystyle r : \ 3x+2y-1=0$

Yapmamız gereken ilk şey doğrunun yön vektörünü belirlemektir. Bu durumda çizgi genel (veya örtülü) bir denklem biçiminde tanımlanır, bu nedenle çizginin yön vektörünün Kartezyen koordinatları çizginin A ve B katsayıları ile elde edilebilir:

$\vv{\text{v}}_r =(-B,A)=(-2,3)$

Doğrunun yön vektörünü bildiğimizde ona dik bir vektör hesaplamamız gerekir. Bunu yapmak için, vektörün koordinatlarını girmeniz ve bunlardan birinin (istediğiniz işaret) işaretini değiştirmeniz yeterlidir:

$\vv{\text{v}}_\perp =(3,2)$

Artık doğrunun yön vektörünü biliyoruz. Bu nedenle doğrunun örtülü denklemi aşağıdaki gibi olacaktır:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (3,2) \end{array} \right\}\longrightarrow \begin{array}{l}A=2 \\[2ex] B=-3 \end{array}$

$Ax+By+C \ \longrightarrow \ 2x-3y+C=0$

Bu nedenle C parametresini belirlemek yeterlidir. Bunu yapmak için düz çizgiye ait noktayı denkleminde yerine koyarız ve ortaya çıkan denklemi çözeriz:

$P(5,-1)$

$2x-3y+C=0 \ \xrightarrow{x=5 \ ; \ y=-1} \ 2\cdot 5-3\cdot (-1)+C=0$

$10+3+C=0$

$13+C=0$

$C=-13$

Sonuç olarak dik çizginin denklemi şu şekildedir:

$\bm{2x-3y-13=0}$

Çizginin eğiminden

Belirli bir doğruya dik olan bir doğruyu bulmanın başka bir yolu da onun eğimidir. Bu tür bir sorunun nasıl çözüldüğünü bir örnekle görelim:

Çizgiye dik çizgiyi hesaplayın
$r$

noktadan geçen şey

$P(0,1)$

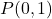
. düz olmak

$r:$

$\displaystyle r : \ y=4x-3$

Çizginin eğimi

$r$

Doğu:

$m_r = 4$

Doğrunun eğimini öğrendikten sonra dik doğrunun eğimini bulmamız gerekir. Yukarıdaki bölümlerde gördüğümüz gibi birbirine dik iki doğrunun eğimleri terstir ve işaretleri değişmiştir. Bu nedenle dik çizginin eğimini belirlemek için bulunan eğimi ters çevirip işaretini değiştirmemiz gerekir:

$m_\perp =-\cfrac{1}{4}$

Bu nedenle dik çizginin açık denklemi aşağıdaki gibi olacaktır:

$y= mx+n$

$y=-\cfrac{1}{4} \ x + n$

Son olarak, noktanın koordinatlarını çizgi denkleminde yerine koyarak dik çizginin orijinindeki koordinatı hesaplarız:

$P(0,1)$

$y=-\cfrac{1}{4} \ x + n \ \xrightarrow{x=0 \ ; \ y=1} \ 1 =-\cfrac{1}{4}\cdot 0 + n$

$1 = n$

Kısaca dik çizginin denklemi:

$\bm{y=-}\mathbf{\cfrac{1}{4}} \ \bm{x + 1}$

Dik çizgilerin özellikleri

Tüm dikey çizgiler aşağıdaki özelliklere sahiptir:

Simetrik ilişki : Bir doğru başka bir doğruya dikse, o doğru ilk doğruya da diktir.

$r \bm{\perp} s \ \longrightarrow \ s \bm{\perp} r$

Yansımama özelliği : Açıkçası hiçbir doğru kendisine dik olamaz.

$r \ \cancel{\bm{\perp}}} \ r$

Teorem: Öklid geometrisinde (R2’de), üçüncü bir çizgiye dik olan herhangi bir çizgi çifti zorunlu olarak paralel olmalıdır. Yani, bir doğru başka bir doğruya dikse ve o doğru da üçüncü bir doğruya dikse, ilk ve son doğrular paraleldir.

Dik doğruların çözülmüş problemleri

1. Egzersiz

Aşağıdaki doğrulardan hangisi doğruya diktir

$r: y=3x+4$

$a : \ y=3x-\cfrac{1}{3}$

$b : \ y=-\cfrac{1}{3} \ x+5$

$c : \ y=-4x-3$

$d : \ y=\cfrac{1}{3} \ x-5$

$e : \ y=-\cfrac{1}{3} \ x-2$

Çözüme bakın

Çizginin eğimi

$r$

$m_r=3$

Ve birbirine dik iki doğrunun eğimleri ters ve zıt işaretlidir, dolayısıyla doğruya dik olan herhangi bir doğrunun eğimi

$r$

olmalıdır:

$m_\perp=-\cfrac{1}{3}$

Böylece çizgiye dik çizgiler

$r$

eğimi eşit olanlardır

$-\cfrac{1}{3}$

. Yani çizgiler

$\bm{b}$

$\bm{e}.$

Alıştırma 2

Aşağıdaki iki çizginin dik olup olmadığını belirleyin:

$\displaystyle r: \ \begin{cases} x=4-t \\[2ex] y=1-3t \end{cases}\qquad \qquad s: \ \cfrac{x-2}{4} = \cfrac{y+3}{6}$

Çözüme bakın

doğru

$r$

söz konusu çizginin yön vektörünün bileşenleri parametrenin önündeki sayılar olacak şekilde parametrik bir denklem biçiminde ifade edilir

$t:$

$\vv{\text{v}}_r =(-1,-3)$

Öte yandan düz çizgi

$s$

sürekli bir denklem biçiminde tanımlanır, dolayısıyla yön vektörünün koordinatları paydaların sayılarıdır:

$\vv{\text{v}}_s =(4,6)$

Her çizginin yön vektörünü bildiğimizde, iki vektörün çarpımını hesaplayarak çizgilerin dik olup olmadığını kontrol edebiliriz:

$\vv{\text{v}}_r \cdot \vv{\text{v}}_s = (-1,-3)\cdot (4,6) = -1\cdot 4 + (-3)\cdot 6= -22 \bm{\neq 0}$

İki vektörün nokta çarpımı sıfırdan farklı olduğundan çizgiler dik değildir .

Alıştırma 3

Çizgiye dik olan çizgiyi bulun

$r$

noktadan geçen şey

$P(-2,1)$

. düz olmak

$r:$

$\displaystyle r : \ 4x-y+5=0$

Çözüme bakın

Yapmamız gereken ilk şey doğrunun yön vektörünü belirlemektir. Bu durumda çizgi genel (veya örtülü) bir denklem biçiminde tanımlanır, dolayısıyla yön vektörü şöyledir:

$\vv{\text{v}}_r =(-B,A)=(1,4)$

Doğrunun yön vektörünü bildiğimizde ona dik bir vektör hesaplamamız gerekir. Bunu yapmak için, vektörün koordinatlarını girmeniz ve bunlardan birinin (istediğiniz işaret) işaretini değiştirmeniz yeterlidir:

$\vv{\text{v}}_\perp =(4,-1)$

Bu nedenle doğrunun örtülü denklemi aşağıdaki gibi olacaktır:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}_\perp= (4,-1) \end{array} \right\}\longrightarrow \begin{array}{l}A=-1 \\[2ex] B=-4 \end{array}$

$Ax+By+C \ \longrightarrow \ -x-4y+C=0$

Bu nedenle bilinmeyen C’yi belirlemek yeterlidir. Bunu yapmak için doğrunun geçtiği noktayı denklemin yerine koyarız:

$P(-2,1)$

$-x-4y+C=0 \ \xrightarrow{x=-2 \ ; \ y=1} \ -(-2)-4\cdot 1+C=0$

$2-4+C=0$

$-2+C=0$

$C=2$

Son olarak dik çizginin denklemi:

$\bm{-x-4y+2=0}$

Alıştırma 4

Doğruya dik olan doğrunun nokta-eğim denklemini bulun

$r$

noktadan geçen şey

$P(3,-2)$

. düz olmak

$r:$

$\displaystyle r : \ y=5x+1$

Çözüme bakın

Çizginin eğimi

$r$

Doğu:

$m_r = 5$

Doğrunun eğimini öğrendikten sonra dik doğrunun eğimini bulmamız gerekir. Bunu yapmak için, bulunan eğimi ters çevirin ve işaretini değiştirin:

$m_\perp =-\cfrac{1}{5}$

Son olarak, bulunan eğimi ve noktanın koordinatlarını çizginin nokta-eğim denkleminde yerine koyun:

$y -y_0=m(x-x_0)$

$y-(-2)=-\cfrac{1}{5} (x- 3)$

$\bm{y+2=}\mathbf{-\cfrac{1}{5}}\bm{ (x- 3)}$

Alıştırma 5

doğru

$r$

(2,1) ve (4,2) noktalarından ve doğrudan geçer

$s$

(-1,2) ve (1,-2) noktalarından geçer. Bunların iki dik çizgi olup olmadığını belirleyin.

Çözüme bakın

Bunların iki dik çizgi olup olmadığını kontrol etmek için eğimlerini hesaplayacağız ve sonra dik ilişkiye uyup uymadıklarını göreceğiz. Bir doğrunun eğiminin formülünün şöyle olduğunu unutmayın:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Çizginin eğimi

$r$

Doğu:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{2-1}{4-2} = \cfrac{1}{2}$

Çizginin eğimi

$s$

Doğu:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{-2-2}{1-(-1)} = \cfrac{-4}{2}=-2$

İki doğrunun dikliğini kontrol etmek için bir doğrunun eğiminin diğer eğimin tersi olup olmadığına bakmalıyız. Bu durumda iki eğim terstir ve aynı zamanda zıt işaretlere sahiptir, dolayısıyla iki doğru birbirine diktir.

Alıştırma 6

Değerini hesapla

$k$

böylece aşağıdaki iki çizgi birbirine dik olur:

$\displaystyle r: \ 5x+3y-7=0\qquad \qquad s: \ 4x+ky+1=0$

Çözüme bakın

İki çizgi örtülü (veya genel) bir denklem biçiminde ifade edilir ve çizginin örtülü denkleminin yön vektörü şöyledir:

$Ax+By+C=0$

$\vv{\text{v}} =(-B,A)$

Bu nedenle her çizginin yön vektörü şöyle olacaktır:

$\vv{\text{v}}_r =(-3,5) \qquad \qquad \vv{\text{v}}_s =(-k,4)$

İki doğrunun birbirine dik olması için yön vektörlerinin skaler çarpımının sıfır olması gerekir. Bu nedenle bilinmeyenin değerini bulmak için bu koşulu uygulayacağız.

$k:$