Euler formülü , matematiğin iki temel kavramını birbirine bağlayan matematiksel bir kavramdır: karmaşık sayılar ve trigonometri. Bu onu en önemli kavramsallaştırmalardan biri haline getirir ve matematiğin tamamında en fazla uygulamaya sahiptir. Bu makale boyunca bu formülün neye benzediğini ve sahip olduğu tüm kullanımları göreceğiz.
Euler’in formülü nedir?
Euler formülü, karmaşık sayıları trigonometriyle ilişkilendiren, Euler sayısını temel alan temel bir matematiksel denklemdir. 18. yüzyılda İsviçreli matematikçi Leonhard Euler tarafından keşfedildi ve o zamandan beri fizikten bilgisayar bilimine kadar çeşitli alanlarda kullanıldı.
Euler formülü şu şekilde yazılır: e ix = cos(x) + i sin(x) ; burada e doğal logaritmanın tabanıdır, i hayali birimdir (-1’in karekökü olarak tanımlanır) ve x bir gerçektir sayı. Bu denklem, e ix karmaşık sayısının, cos(x) gerçek sayısı ile sanal sayı i’nin gerçek sayı sin(x) ile çarpımının toplamına eşit olduğunu belirtir.

Euler formülünün önemi, karmaşık sayıların gerçek sayılar ve trigonometri cinsinden ifade edilmesine olanak sağlaması, bunların işlenmesini ve hesaplanmasını kolaylaştırmasıdır.
Euler formülünün kanıtı
Euler formülünün kanıtı, üstel fonksiyon için Taylor serisinin ve kosinüs ve sinüs için trigonometrik özdeşliğin kullanımına dayanmaktadır.
İlk olarak üstel fonksiyon için Taylor serisini ele alıyoruz:

Daha sonra, yukarıdaki denklemde x’i ix ile değiştiririz; burada i sanal birimdir (-1’in karekökü):
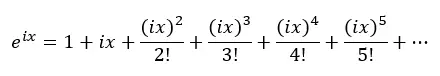
Yani, i’nin kuvvetlerini uyguluyoruz ve önceki denklemde yerine koyuyoruz:
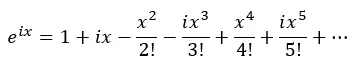
Şimdi gerçek terimleri ve terimleri i ile gruplandırıyoruz:
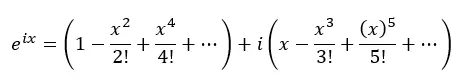
Aslında yukarıdaki parantezlerin her biri kosinüs ve sinüs için Taylor serisidir:
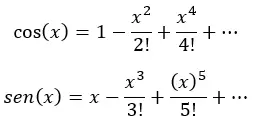
Son olarak, basitleştiririz (parantez içindeki her ifadeyi kosinüs ve sinüs x ile değiştirerek) ve şunu elde ederiz:

Euler formülü örneği
Artık bu matematiksel formülün nasıl çalıştığını bildiğinize göre, aşağıdaki pratik örneği çözmeye çalışmanızı öneririz: e 2i karmaşık sayısını (radyan cinsinden) binom biçiminde ifade edin:
Euler formülünün ana uygulaması, üstel biçimde ifade edilen karmaşık bir sayıyı binom biçimine dönüştürmektir. Bu nedenle şu formülü kullanacağız : e ix = cos(x) + i sin(x)
e 2i = cos(2) + i sin(2)
e2i = -0,416 + 0,909i
Ve sayıyı zaten binom biçiminde elde etmiş olurduk. Buradan karmaşık düzlemde grafiksel gösterimi yapabiliriz. Bunu yapmak için, karmaşık bir sayının, apsis üzerindeki gerçek kısım (x ekseni) ve ordinat üzerindeki sanal kısım (y ekseni) koordinatları kullanılarak karmaşık düzlemde temsil edildiğini anlamak gerekir.
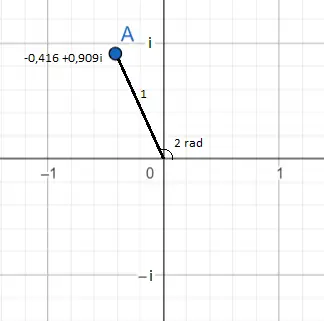
Önceki resimde -0,416 + 0,909i’ye eşit olan e 2i karmaşık sayısı gösterilmektedir. Bu mavi renkli bir nokta olarak görülebilir. Düzlemdeki konumu iki açıdan görülebilir.
Bunlardan ilki ve en belirgini, sayının binom biçiminde temsilidir: -0,416 (apsis üzerinde) ve 0,909 (bilgisayarda). İkincisi ise üstel formdadır : e 2i’nin modülü 1’e eşittir, çünkü e’nin önündeki sayıdır (e’nin önünde bir sayı olmadığı için 1 olduğunu hayal etmeliyiz) ve üssün içinde 2 var, dolayısıyla argüman veya açı iki radyana eşdeğerdir.
Bu son paragrafı tam olarak anlamadıysanız karmaşık sayılar hakkındaki makalemizi okumanızı öneririz. Burada karmaşık bir sayıyı yazmanın farklı yolları ve onun tüm özellikleri hakkında çok derinlemesine bir açıklama yapıyoruz.
Euler formülünün grafiksel gösterimi
Önceki örnekte Euler formülünün nasıl uygulandığını ve karmaşık düzlemde grafiksel olarak nasıl temsil edildiğini görebildiniz. Ancak biraz daha ileri gidersek ve Euler formülüne eşdeğer bir fonksiyonu temsil etmeye çalışırsak, çok ilginç bir şeyle karşılaşırız: yarıçapı 1 olan bir daire üretir:
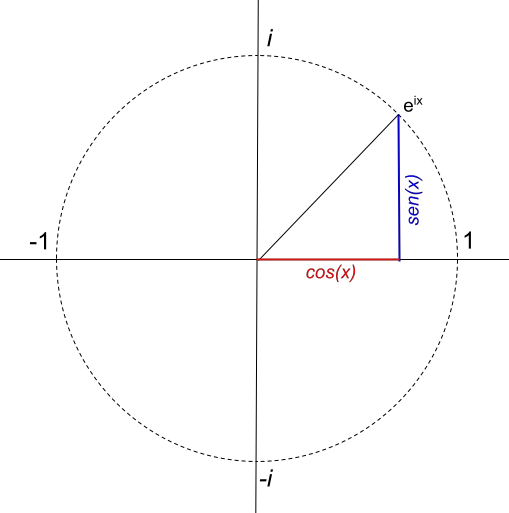
Ancak dairenin yarıçapı doğrudan karmaşık sayının modülünün değerine bağlıdır. Örneğin yarıçapı 4 olan bir daireyi temsil etmek istiyorsak fonksiyon 4e ix olacaktır. Yani 4e ix fonksiyonu şu şekilde temsil edilir:
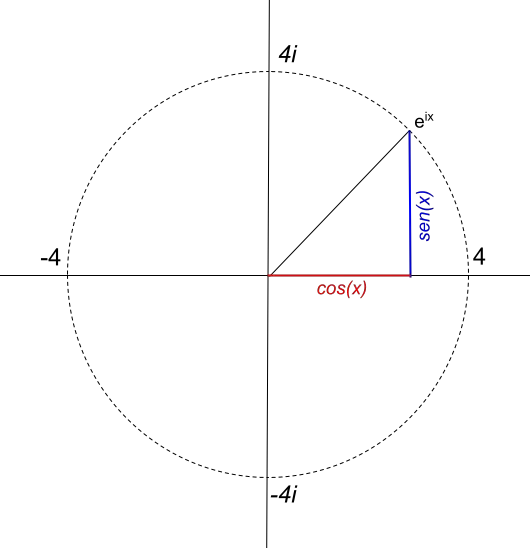
Yarıçapı 1 olan daireye dönersek, e iπ’yi (radyan cinsinden) temsil etmeye karar verirsek, ilk önce şunu hesaplamamız gerekir:
e πi = cos(π) + i sin(π)
eπi = -1 + ben 0
eπi = -1
Ünlü Euler özdeşliği olan e πi = -1’i elde ederiz.
Bundan, e πi karmaşık sayısının -1’e eşit olan tek bir gerçek kısmı olduğu sonucunu çıkarıyoruz. Bu nedenle temsili şu şekilde olacaktır:
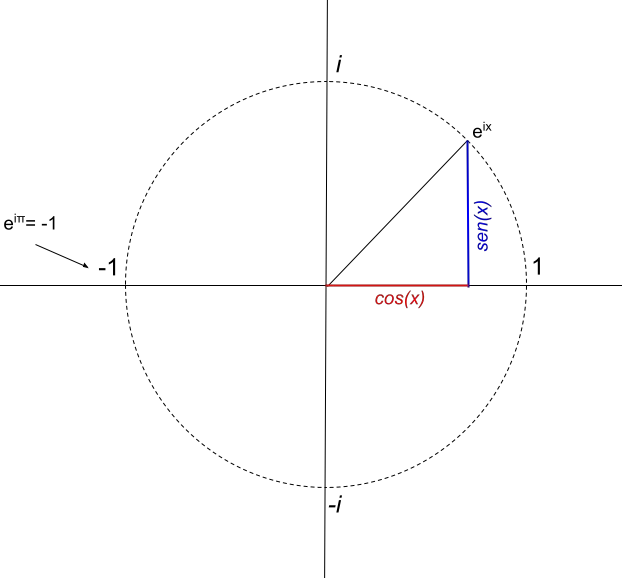
Euler formülünün uygulamaları
- Karmaşık sayılar: Euler formülü, trigonometrik fonksiyonlar ile karmaşık sayılar arasındaki ilişkidir. Bu formülden karmaşık sayıları farklı şekillerde ifade edebiliriz: binom, üstel ve kutupsal.
- Taylor serisi: Taylor serisi fonksiyonlarını genişletmek için Euler formülü kullanılır.
- Lineer Cebir: Lineer cebirin temel tekniklerinden biri olan matris köşegenleştirmesinde Euler formülü kullanılır.
- Diferansiyel ve İntegral Hesap: Matematikte ilgili bir teknik olan diferansiyel denklemlerin çözümünde Euler formülü kullanılır.
Ek olarak, birçok matematik teorisinde ve hatta fizik teoremleri gibi matematik alanı dışındaki kavramlarda da uygulamaları vardır.
sonuçlar
Bu makalede gördüğünüz gibi, Euler formülünün en büyük uygulaması karmaşık sayılardır : sayısal ifadesi ve temsili. Bunun cebirde bazı uygulamaları olduğu doğrudur, ancak aslında karmaşık sayılarla çalışıyorsunuz. Bu nedenle her şeyden önce bunları iyi anlamak önemlidir.
Bununla birlikte, bu kavramı daha iyi anlamanıza yardımcı olduğumuzu umuyoruz. Ve herhangi bir sorunuz varsa veya bir egzersizin nasıl yapılacağını bilmiyorsanız, yorumlarda bize yazmaktan çekinmeyin.