Cramer kuralı - Mathority

Bu sayfada Cramer kuralının ne olduğunu görecek ve ayrıca Cramer kuralına göre denklem sistemlerini çözmeye yönelik örnekler ve alıştırmalar bulacaksınız.

Cramer kuralı nedir?

Cramer kuralı, denklem sistemlerini determinantlarla çözmek için kullanılan bir yöntemdir. Nasıl kullanıldığına bakalım:

Bir denklem sistemi düşünün:

$\begin{cases} ax+by+cz= \color{red}\bm{j} \\[1.5ex] dx+ey+fz=\color{red}\bm{k} \\[1.5ex] gx+hy+iz = \color{red}\bm{l} \end{cases}$

Sistemin A matrisi ve genişletilmiş A’ matrisi şunlardır:

$\displaystyle A= \left( \begin{array}{ccc} a & b & c \\[1.1ex] d & e & f \\[1.1ex] g & h & i \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} a & b & c & \color{red}\bm{j} \\[1.1ex] d & e & f & \color{red}\bm{k} \\[1.1ex] g & h & i & \color{red}\bm{l} \end{array} \right)$

Cramer kuralı bir denklem sisteminin çözümünün şöyle olduğunu söylüyor:

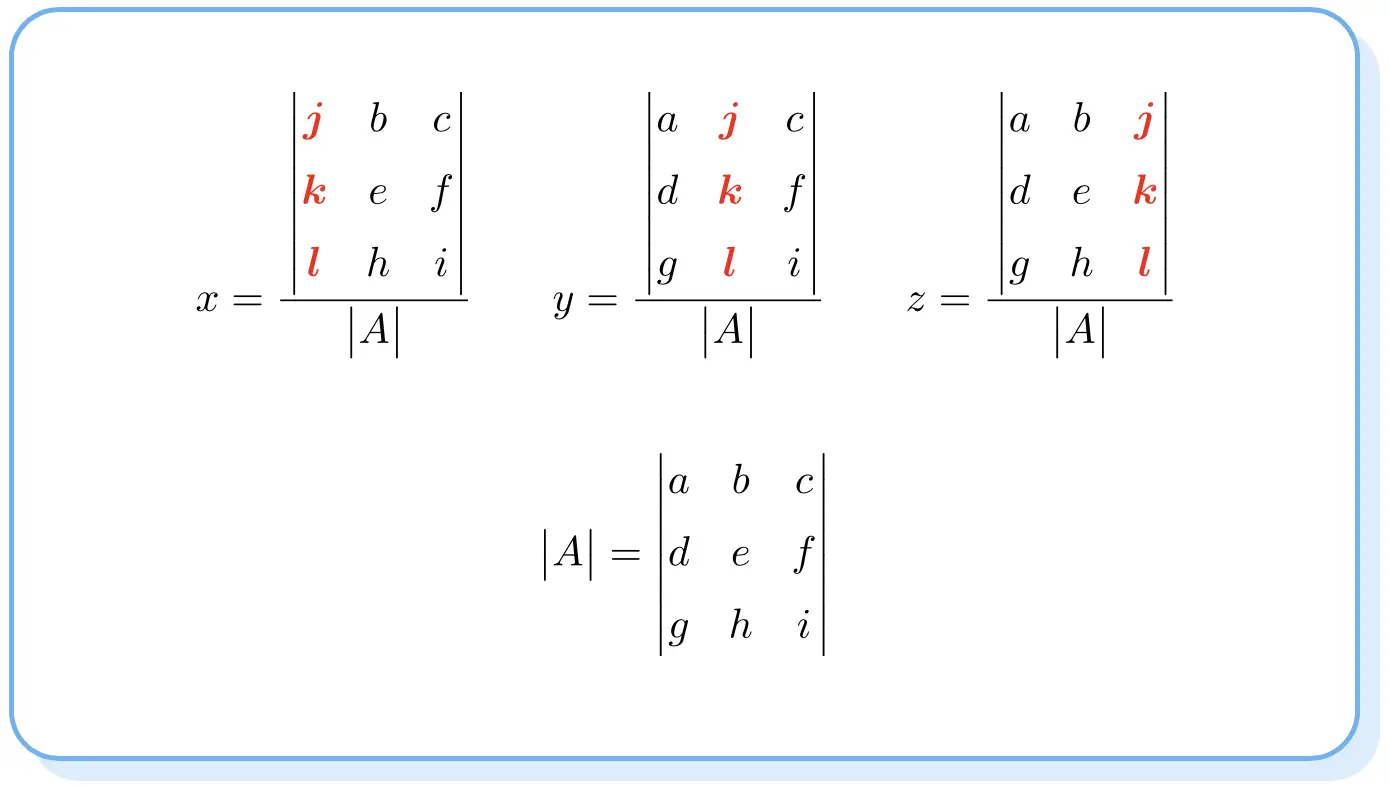
cramer kuralı nedir, cramer kuralı açıklaması

Payların determinantlarının A matrisinin determinantına benzediğini ancak her bilinmeyenin sütununu bağımsız terimlerin sütununa değiştirdiğini unutmayın.

Bu nedenle doğrusal denklem sistemlerini çözmek için Cramer kuralı kullanılır. Ancak bildiğiniz gibi bir denklem sistemini çözmenin birçok yolu vardır; örneğin Gauss Jordan’ın yöntemi iyi bilinmektedir.

Aşağıda Cramer kuralıyla veya bazen Kramer kuralı olarak da yazılan doğrusal denklem sistemlerini çözme örnekleri verilmiştir.

Örnek 1: belirlenen uyumlu sistem (SCD)

Aşağıdaki 3 bilinmeyenli 3 denklemden oluşan sistemi Cramer kuralını kullanarak çözün:

$\begin{cases} 2x+y+3z= 1 \\[1.5ex] 3x-2y-z=0 \\[1.5ex] x+3y+2z = 5\end{cases}$

İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini yaparız:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & 1 \\[1.1ex] 3 & -2 & -1 & 0 \\[1.1ex] 1 & 3 & 2 & 5 \end{array} \right)$

Şimdi ne tür bir sistem olduğunu görmek için iki matrisin sırasını hesaplıyoruz. A’nın rütbesini hesaplamak için tüm matrisin 3×3 determinantını hesaplıyoruz (Sarrus kuralını kullanarak) ve 0 verip vermediğine bakıyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =-8-1+27+6+6-6 = 24 \neq 0$

A’nın determinantı 0’dan farklıdır, dolayısıyla A matrisinin derecesi 3’tür.

$\displaystyle rg(A)=3$

Dolayısıyla A’ matrisi de rütbe 3’tedir , çünkü derece 4 olamaz ve en azından A matrisiyle aynı derecede olmalıdır.

$\displaystyle rg(A')=3$

A matrisinin boyutu, A’ matrisinin boyutuna ve sistemin bilinmeyenlerinin sayısına (3) eşittir, dolayısıyla Rouché-Frobenius teoremine göre bunun belirli bir uyumlu sistem (SCD) olduğunu biliyoruz:

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 3 \\[1.3ex] \color{black}rg(A')=3 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Sistemin bir SCD olduğunu bildiğimizde, onu çözmek için Cramer kuralını uygularız. Bunu yapmak için A matrisinin, determinantının ve A’ matrisinin şöyle olduğunu hatırlayın:

$\displaystyle A= \left( \begin{array}{ccc} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 2 & 1 & 3 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & -1 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & 2 & \color{red}\bm{5} \end{array} \right)$

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 1 & 3 \\[1.1ex] 3 & -2 & -1 \\[1.1ex] 1 & 3 & 2\end{vmatrix} =24$

Bilinmeyeni hesaplamak için

$\displaystyle x$

Cramer kuralıyla A’nın determinantının ilk sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} \color{red}\bm{1} & 1 & 3 \\[1.1ex] \color{red}\bm{0} & -2 & -1 \\[1.1ex] \color{red}\bm{5} & 3 & 2 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{24}{24} = \bm{1}$

Bilinmeyeni hesaplamak için

$\displaystyle y$

Cramer kuralıyla A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 2 & \color{red}\bm{1} & 3 \\[1.1ex] 3 & \color{red}\bm{0} & -1 \\[1.1ex] 1 & \color{red}\bm{5} & 2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{48}{24} = \bm{2}$

Hesaplamak

$\displaystyle z$

Cramer kuralıyla A’nın determinantının üçüncü sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 2 & 1 & \color{red}\bm{1} \\[1.1ex] 3 & -2 & \color{red}\bm{0} \\[1.1ex] 1 & 3 & \color{red}\bm{5}\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-24}{24} = \bm{-1}$

Bu nedenle denklem sisteminin çözümü şu şekildedir:

$\displaystyle \bm{x = 1 \qquad y=2 \qquad z = -1}$

Örnek 2: Belirsiz Uyumlu Sistem (ICS)

Cramer kuralını kullanarak aşağıdaki denklem sistemini çözün:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex] x+5y+3z = 1 \end{cases}$

İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini yaparız:

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & 2 & 4 & 1 \\[1.1ex] -2 & 3 & -1 & 0 \\[1.1ex] 1 & 5 & 3 & 1 \end{array} \right)$

Şimdi iki matrisin aralığını hesaplıyoruz ve böylece ne tür bir sistem olduğunu görebiliriz. A’nın rütbesini hesaplamak için tüm matrisin determinantını hesaplıyoruz (Sarrus kuralını kullanarak) ve 0 olup olmadığını kontrol ediyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 & 4 \\[1.1ex] -2 & 3 & -1 \\[1.1ex] 1 & 5 & 3\end{vmatrix} = 27-2-40-12+15+12= 0$

Determinant 0 verir, dolayısıyla A matrisinin derecesi 3 değildir. Ancak 0’dan farklı 2×2 determinantı vardır:

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

Yani A matrisinin derecesi 2’dir :

$\displaystyle rg(A)=2$

A matrisinin boyutunu bildiğimizde, A’ matrisinin boyutunu hesaplarız. İlk 3 sütunun determinantı 0 verir, dolayısıyla A’ matrisindeki diğer olası 3×3 determinantları deneriz:

$\displaystyle \begin{vmatrix} 2 & 4 & 1 \\[1.1ex] 3 & -1 & 0 \\[1.1ex] 5 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 4 & 1 \\[1.1ex] -2 & -1 & 0 \\[1.1ex] 1 & 3 & 1 \end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & 2 & 1 \\[1.1ex] -2 & 3 & 0 \\[1.1ex] 1 & 5 & 1 \end{vmatrix} = 0$

3. dereceden tüm determinantlar 0 verir. Ancak, A’ matrisinin A matrisiyle aynı 0 olmayan 2×2 determinantına sahip olduğu açıktır:

$\displaystyle \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3 \end{vmatrix} =9-(-4)=13\neq 0$

Bu nedenle A’ matrisi de rütbe 2’dedir :

$\displaystyle rg(A')=2$

Yani, A matrisinin rütbesi A’ matrisinin rütbesine eşit olduğundan, ancak bu ikisi (3) sisteminin bilinmeyen sayısından küçük olduğundan, Rouché-Frobenius teoreminden şunu biliyoruz: Bu Belirsiz Olarak Uyumlu Bir Sistemdir (ICS):

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 3 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = 2 \ < \ n =3 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCI}\phantom{^9_9}} \end{array}$

Uyumlu bir belirsiz sistemi (SCI) çözmek istediğimizde, sistemi dönüştürmemiz gerekir: önce bir denklemi ortadan kaldırırız, sonra bir değişkeni λ’ya (genellikle z değişkeni) dönüştürürüz ve son olarak λ’lı terimleri bir araya getiririz. bağımsız terimler.

Sistemi dönüştürdükten sonra Cramer kuralını uygularız ve sistemin çözümünü λ’nın bir fonksiyonu olarak elde ederiz.

Bu durumda son denklemi sistemden kaldıracağız :

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \\[1.5ex]\cancel{x+5y+3z = 1} \end{cases} \longrightarrow \quad \begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0\end{cases}$

Şimdi z değişkenini λ’ya dönüştürelim:

$\begin{cases} 3x+2y+4z=1 \\[1.5ex] -2x+3y-z=0 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x+2y+4\lambda=1 \\[1.5ex] -2x+3y-\lambda=0\end{cases}$

Ve λ’lı terimleri bağımsız terimlerle birlikte koyarız:

$\begin{cases} 3x+2y=1-4\lambda \\[1.5ex] -2x+3y=\lambda \end{cases}$

Bu nedenle, sistemin A matrisi ve A’ matrisi kalır:

$\displaystyle A= \left( \begin{array}{ccc} 3 & 2 \\[1.1ex] -2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & 2 & 1 -4\lambda \\[1.1ex] -2 & 3 & \lambda \end{array} \right)$

Son olarak sistemi dönüştürdükten sonra Cramer kuralını uyguluyoruz . Bu nedenle A’nın determinantını çözüyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & 2 \\[1.1ex] -2 & 3\end{vmatrix} = 13$

Bilinmeyeni hesaplamak için

$\displaystyle x$

Cramer kuralıyla A’nın determinantının ilk sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1 -4\lambda & 2 \\[1.1ex] \lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3(1-4\lambda) -2\lambda}{13} = \cfrac{\bm{3-14\lambda} }{\bm{13}}$

Bilinmeyeni hesaplamak için

$\displaystyle y$

Cramer kuralıyla A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 1 -4\lambda \\[1.1ex]-2& \lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3\lambda -\bigl(-2(1-4\lambda)\bigr)}{13}= \cfrac{3\lambda -\bigl(-2+8\lambda\bigr)}{13} = \cfrac{\bm{2-5\lambda} }{\bm{13}}$

Denklem sisteminin çözümü λ’nın bir fonksiyonu olsa da, bu bir SCI olduğundan ve dolayısıyla sonsuz sayıda çözümü olduğundan:

$\displaystyle \bm{x =} \cfrac{\bm{3-14\lambda} }{\bm{13}} \qquad \bm{y=}\cfrac{\bm{2-5\lambda} }{\bm{13}} \qquad \bm{z = \lambda}$

Cramer Kuralı Sorunları Çözdü

1. Egzersiz

Aşağıdaki 2 bilinmeyenli iki denklem sistemini çözmek için Cramer kuralını uygulayın:

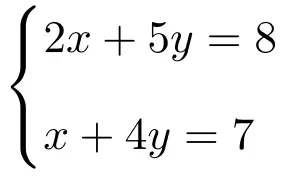
egzersiz Cramer'in 2x2 kuralıyla adım adım çözüldü

Çözüme bakın

Yapılacak ilk şey sistemin A matrisi ve genişletilmiş A’ matrisidir:

$\displaystyle A= \left( \begin{array}{cc} 2 & 5 \\[1.1ex] 1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 2 & 5 & 8 \\[1.1ex] 1 & 4 & 7 \end{array}\right)$

Şimdi A matrisinin rütbesini bulmalıyız. Bunu yapmak için tüm matrisin determinantının 0’dan farklı olup olmadığını kontrol ederiz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 2 & 5 \\[1.1ex] 1 & 4 \end{vmatrix} = 8-5=3 \bm{\neq 0}$

Matrisin 0’dan farklı bir 2×2 determinantı olduğundan, A matrisinin derecesi 2’dir:

$\displaystyle rg(A)=2$

A’nın rütbesini bildiğimizde, A”nın rütbesini hesaplarız. Bu en azından 2. basamakta olacaktır, çünkü az önce 0’dan farklı 2. basamakta bir determinantı olduğunu gördük. Ayrıca 3×3’lük bir determinant yapamayacağımız için 3. basamakta olamaz. Bu nedenle A’ matrisi de 2. sıradadır:

$\displaystyle rg(A')=2$

Bu nedenle, Rouché-Frobenius teoremini uygulayarak bunun uyumlu bir belirli sistem (SCD) olduğunu biliyoruz çünkü A’nın aralığı, A’ aralığına ve bilinmeyenlerin sayısına eşittir.

$\displaystyle \begin{array}{c} \begin{array}{c} \color{black}rg(A) = 2 \\[1.3ex] \color{black}rg(A')=2 \\[1.3ex] \color{black}\text{N\'umero de inc\'ognitas} = 2 \end{array}} \\ \\ \color{blue} \boxed{ \color{black}\phantom{^9_9} rg(A) = rg(A') = n = 2 \color{blue} \ \bm{\longrightarrow} \ \color{black} \bm{SCD}\phantom{^9_9}} \end{array}$

Sistemin bir SCD olduğunu bildiğimizde, onu çözmek için Cramer kuralını uygularız.

Bilinmeyeni hesaplamak için

$\displaystyle x$

Cramer kuralıyla A’nın determinantının ilk sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 \\[1.1ex] 7 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-3}{3} = \bm{-1}$

Bilinmeyeni hesaplamak için

$\displaystyle y$

Cramer kuralıyla A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}2 & 8 \\[1.1ex] 1 & 7\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{6}{3} = \bm{2}$

Bu nedenle denklem sisteminin çözümü şu şekildedir:

$\displaystyle \bm{x = -1 \qquad y=2}$

Alıştırma 2

Cramer kuralını kullanarak aşağıdaki 3 bilinmeyenli üç denklem sisteminin çözümünü bulun:

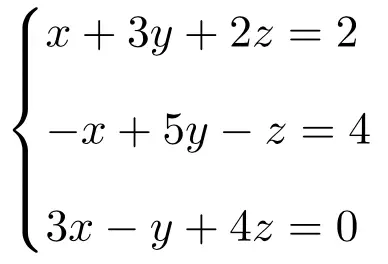
3x3 denklem sistemi Cramer kuralının çözülmüş alıştırması

Çözüme bakın

İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini yaparız:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 3 & 2\\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 3 & 2 & 2 \\[1.1ex] -1 & 5 & -1 & 4 \\[1.1ex] 3 & -1 & 4 & 0 \end{array}\right)$

Şimdi A matrisinin rütbesini 3×3 matrisin determinantını Sarrus kuralıyla hesaplayarak buluyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & -1\\[1.1ex] 3 & -1 & 4 \end{vmatrix} = 20-9+2-30-1+12=-6 \bm{\neq 0}$

0’dan farklı 3. dereceden bir determinantı olan matris, A matrisi 3. derecedendir:

$\displaystyle rg(A)=3$

sonuç olarak, A’ matrisi de 3. sıradadır:

$\displaystyle rg(A')=3$

Bu nedenle, Rouché-Frobenius teoremini kullanarak bunun uyumlu bir belirli sistem (SCD) olduğunu biliyoruz çünkü A’nın aralığı, A’ aralığına ve bilinmeyenlerin sayısına eşittir.

Sistemin bir SCD olduğunu bildiğimizde, sistemi çözmek için Cramer kuralını uygulamamız gerekir.

Bilinmeyeni hesaplamak için

$\displaystyle x$

Cramer kuralıyla A’nın determinantının ilk sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 2 & 3 & 2 \\[1.1ex] 4 & 5 & -1\\[1.1ex]0 & -1 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-18}{-6} = \bm{3}$

Bilinmeyeni hesaplamak için

$\displaystyle y$

Cramer kuralıyla A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}1 & 2 & 2 \\[1.1ex] -1 & 4 & -1\\[1.1ex] 3 & 0 & 4\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-6}{-6} = \bm{1}$

Hesaplamak

$\displaystyle z$

Cramer kuralıyla A’nın determinantının üçüncü sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} 1 & 3 & 2 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 3 & -1 & 0\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{12}{-6} = \bm{-2}$

Bu nedenle denklem sisteminin çözümü şu şekildedir:

$\displaystyle \bm{x =3 \qquad y=1 \qquad z=-2}$

Alıştırma 3

Aşağıdaki 3 bilinmeyenli üç denklem sisteminin çözümünü Cramer kuralını kullanarak hesaplayın:

Çözüme bakın

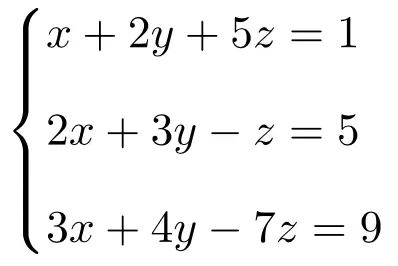
İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini yaparız:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 1 & 2 & 5 & 1 \\[1.1ex] 2 & 3 & -1 & 5 \\[1.1ex] 3 & 4 & -7 & 9 \end{array}\right)$

A matrisinin boyutunu hesaplıyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 & 5\\[1.1ex] 2 & 3 & -1 \\[1.1ex] 3 & 4 & -7 \end{vmatrix} =-21-6+40-45+4+28=0$

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

$\displaystyle rg(A)=2$

A matrisinin boyutunu bildiğimizde, A’ matrisinin boyutunu hesaplarız. İlk 3 sütunun determinantı 0 verir, dolayısıyla A’ matrisindeki diğer olası 3×3 determinantları deneriz:

$\displaystyle \begin{vmatrix} 2 & 5 & 1 \\[1.1ex] 3 & -1 & 5 \\[1.1ex] 4 & -7 & 9 \end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 5 & 1 \\[1.1ex] 2 & -1 & 5 \\[1.1ex] 3 & -7 & 9\end{vmatrix} = 0 \qquad \begin{vmatrix} 1 & 2 & 1 \\[1.1ex] 2 & 3 & 5 \\[1.1ex] 3 & 4 & 9 \end{vmatrix} = 0$

3. dereceden tüm determinantlar 0 verir. Bununla birlikte, A’ matrisi, A matrisiyle aynı 2×2 0 olmayan determinanta sahiptir:

$\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3 \end{vmatrix} = 3-4 = -1 \neq 0$

Bu nedenle A’ matrisi de 2. sıradadır:

$\displaystyle rg(A')=2$

A matrisinin rütbesi A’ matrisinin rütbesine eşit olduğundan, ancak bu ikisi sistem (3)’ün bilinmeyen sayısından az olduğundan, bunun bir Belirsiz Uyumlu Sistem (ICS) olduğunu Rouché-Frobenius teoreminden biliyoruz:

Bir ICS sistemi olarak bir denklemi ortadan kaldırmamız gerekiyor. Bu durumda son denklemi sistemden kaldıracağız :

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \\[1.5ex]\cancel{3x+4y-7z = 9} \end{cases} \longrightarrow \quad \begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5\end{cases}$

Şimdi z değişkenini λ’ya dönüştürelim:

$\begin{cases} x+2y+5z=1 \\[1.5ex] 2x+3y-z=5 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} x+2y+5\lambda=1 \\[1.5ex] 2x+3y-\lambda=5\end{cases}$

Ve λ’lı terimleri bağımsız terimlerle birlikte koyarız:

$\begin{cases} x+2y=1-5\lambda\\[1.5ex] 2x+3y=5+\lambda \end{cases}$

Öyle ki sistemin A matrisi ve A’ matrisi şöyle kalır:

$\displaystyle A= \left( \begin{array}{ccc} 1 & 2 \\[1.1ex] 2 & 3 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 1 & 2 & 1 -5\lambda \\[1.1ex] 2 & 3 &5+\lambda \end{array} \right)$

Son olarak sistemi dönüştürdükten sonra Cramer kuralını uyguluyoruz . Bu nedenle A’nın determinantını çözüyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 1 & 2 \\[1.1ex] 2 & 3\end{vmatrix} =-1$

Bilinmeyeni hesaplamak için

$\displaystyle x$

Cramer kuralıyla A’nın determinantının ilk sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 1-5\lambda & 2 \\[1.1ex] 5+\lambda & 3 \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{3-15\lambda -(10+2\lambda)}{-1} = \cfrac{-7-17\lambda}{-1} = \bm{7+17\lambda}$

Bilinmeyeni hesaplamak için

$\displaystyle y$

Cramer kuralıyla A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 1 & 1-5\lambda \\[1.1ex] 2 & 5+\lambda \end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{5+\lambda -(2-10\lambda)}{-1}= \cfrac{3+11\lambda}{-1} = \bm{-3-11\lambda}$

Denklem sisteminin çözümü λ’nın bir fonksiyonu olsa da, bu bir SCI olduğundan ve dolayısıyla sonsuz sayıda çözümü olduğundan:

$\displaystyle \bm{x =7+17\lambda} \qquad \bm{y=-3-11\lambda} \qquad \bm{z = \lambda}$

Alıştırma 4

3 bilinmeyenli üç denklemli bir sistemin aşağıdaki problemini Cramer kuralını uygulayarak çözün:

$\begin{cases} -2x+5y+z=8 \\[1.5ex] 6x+2y+4z=4 \\[1.5ex] 3x-2y+z = -2 \end{cases}$

Çözüme bakın

Öncelikle sistemin A matrisini ve genişletilmiş A’ matrisini oluşturuyoruz:

$\displaystyle A= \left( \begin{array}{ccc}-2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1\end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} -2 & 5 & 1 & 8 \\[1.1ex] 6 & 2 & 4 & 4 \\[1.1ex] 3 & -2 & 1 & -2 \end{array}\right)$

Şimdi 3×3’lük matrisin determinantını Sarrus kuralını kullanarak hesaplayarak A matrisinin rütbesini hesaplayalım:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} -2 & 5 & 1 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & 1 \end{vmatrix} = -4+60-12-6-16-30=-8 \bm{\neq 0}$

0’dan farklı 3. dereceden bir determinantı olan matris, A matrisi 3. derecedendir:

$\displaystyle rg(A)=3$

sonuç olarak, A’ matrisi de 3. sıradadır, çünkü en azından A matrisiyle aynı sırada olmalıdır ve 3×4 boyutunda bir matris olduğu için 4. sırada olamaz.

$\displaystyle rg(A')=3$

Bu nedenle, Rouché-Frobenius teoremini kullanarak bunun belirli uyumlu bir sistem (SCD) olduğu sonucuna varırız çünkü A’nın aralığı, A’ aralığına ve bilinmeyenlerin sayısına eşittir.

Sistemin bir SCD olduğunu bildiğimizde, sistemi çözmek için Cramer kuralını uygulamamız gerekir.

Bilinmeyeni hesaplamak için

$\displaystyle x$

Cramer kuralıyla A’nın determinantının ilk sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 8 & 5 & 1 \\[1.1ex] 4 & 2 & 4 \\[1.1ex] -2 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{16}{-8} = \bm{-2}$

Bilinmeyeni hesaplamak için

$\displaystyle y$

Cramer kuralıyla A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix}-2 & 8 & 1 \\[1.1ex] 6 & 4 & 4 \\[1.1ex] 3 & -2 & 1\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{0}{-6} = \bm{0}$

Hesaplamak

$\displaystyle z$

Cramer kuralıyla A’nın determinantının üçüncü sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{z} = \cfrac{\begin{vmatrix} -2 & 5 & 8 \\[1.1ex] 6 & 2 & 4 \\[1.1ex] 3 & -2 & -2\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-32}{-8} = \bm{4}$

Dolayısıyla doğrusal denklem sisteminin çözümü şu şekildedir:

$\displaystyle \bm{x =-2 \qquad y=0 \qquad z=4}$

Alıştırma 5

Cramer kuralını kullanarak aşağıdaki doğrusal denklem sistemini çözün:

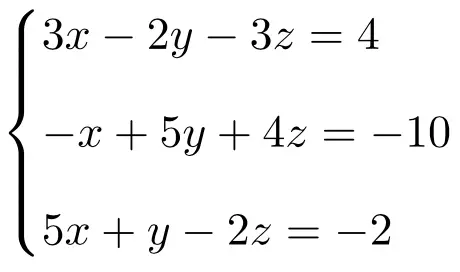
Cramer kuralıyla bir denklem sistemini çözme örneği

Çözüme bakın

İlk önce sistemin A matrisini ve genişletilmiş A’ matrisini yaparız:

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{array} \right) \qquad A'= \left( \begin{array}{ccc|c} 3 & -2 & -3 & 4 \\[1.1ex] -1 & 5 & 4 & -10 \\[1.1ex] 5 & 1 & -2 & -2 \end{array}\right)$

A matrisinin boyutunu hesaplıyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix} 3 & -2 & -3 \\[1.1ex] -1 & 5 & 4 \\[1.1ex] 5 & 1 & -2 \end{vmatrix} =-30-40+3+75-12+4=0$

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 15- (2)= 13 \neq 0$

$\displaystyle rg(A)=2$

A matrisinin boyutunu bildiğimizde, A’ matrisinin boyutunu hesaplarız. İlk 3 sütunun determinantı 0 verir, dolayısıyla A’ matrisindeki diğer olası 3×3 determinantları deneriz:

$\displaystyle \begin{vmatrix} -2 & -3 & 4 \\[1.1ex] 5 & 4 & -10 \\[1.1ex] 1 & -2 & -2 \end{vmatrix} = 0 \qquad \begin{vmatrix}3 & -3 & 4 \\[1.1ex] -1 & 4 & -10 \\[1.1ex] 5 & -2 & -2\end{vmatrix} = 0 \qquad \begin{vmatrix} 3 & -2 & 4 \\[1.1ex] -1 & 5 & -10 \\[1.1ex] 5 & 1 &-2\end{vmatrix} = 0$

3. mertebeden tüm determinantlar 0 verir. Ancak, A’ matrisinin 0 dışında 2. mertebeden aynı determinantı A matrisiyle aynıdır:

$\displaystyle \begin{vmatrix} 3 & -2 \\[1.1ex] -1 & 5 \end{vmatrix} = 13 \neq 0$

Bu nedenle A’ matrisi de 2. sıradadır:

$\displaystyle rg(A')=2$

A matrisinin rütbesi, A’ matrisinin rütbesine eşittir ancak bu ikisi sistemin bilinmeyen sayısından (3) küçüktür, dolayısıyla Rouché-Frobenius teoreminden bunun Belirsiz Sistem Uyumlu (SCI) olduğunu biliyoruz. :

Bir ICS sistemi olarak bir denklemi ortadan kaldırmak zorundayız. Bu durumda son denklemi sistemden kaldıracağız :

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \\[1.5ex]\cancel{5x+y-2z = -2} \end{cases} \longrightarrow \quad \begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10\end{cases}$

Şimdi z değişkenini λ’ya dönüştürelim:

$\begin{cases} 3x-2y-3z=4 \\[1.5ex] -x+5y+4z=-10 \end{cases} \xrightarrow{z \ = \ \lambda}\quad \begin{cases} 3x-2y-3\lambda=4 \\[1.5ex] -x+5y+4\lambda=-10\end{cases}$

Ve λ’lı terimleri bağımsız terimlerle birlikte koyarız:

$\begin{cases} 3x-2y=4+3\lambda \\[1.5ex] -x+5y=-10-4\lambda\end{cases}$

Öyle ki sistemin A matrisi ve A’ matrisi şöyle kalır:

$\displaystyle A= \left( \begin{array}{ccc} 3 & -2 \\[1.1ex] -1 & 5 \end{array} \right) \qquad A'= \left( \begin{array}{cc|c} 3 & -2 & 4+3\lambda \\[1.1ex] 1 & 5 &-10-4\lambda \end{array} \right)$

Son olarak sistemi dönüştürdükten sonra Cramer kuralını uyguluyoruz . Bu nedenle A’nın determinantını çözüyoruz:

$\displaystyle \begin{vmatrix}A \end{vmatrix}= \begin{vmatrix}3& -2 \\[1.1ex] -1 & 5\end{vmatrix} =13$

Bilinmeyeni hesaplamak için

$\displaystyle x$

Cramer kuralıyla A’nın determinantının ilk sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{x} = \cfrac{\begin{vmatrix} 4+3\lambda & -2 \\[1.1ex]-10-4\lambda & 5\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{20+15\lambda -(20+8\lambda)}{13} = \cfrac{\bm{7\lambda}}{\bm{13}}$

Bilinmeyeni hesaplamak için

$\displaystyle y$

Cramer kuralıyla A’nın determinantının ikinci sütununu bağımsız terimler sütunuyla değiştirip A’nın determinantına bölüyoruz:

$\displaystyle \bm{y} = \cfrac{\begin{vmatrix} 3 & 4+3\lambda \\[1.1ex] -1 & -10-4\lambda\end{vmatrix}}{\begin{vmatrix} A \end{vmatrix}} = \cfrac{-30-12\lambda -(-4-3\lambda)}{13}= \cfrac{\bm{-26-9\lambda}}{\bm{13}}$

Dolayısıyla denklem sisteminin çözümü λ’nın bir fonksiyonudur, çünkü bu bir SCI’dir ve dolayısıyla sistemin sonsuz sayıda çözümü vardır:

$\displaystyle \bm{x=} \cfrac{\bm{7\lambda}}{\bm{13}} \qquad \bm{y=} \cfrac{\bm{-26-9\lambda}}{\bm{13}} \qquad \bm{z = \lambda}$

Cramer kuralı nedir?

Örnek 1: belirlenen uyumlu sistem (SCD)

Örnek 2: Belirsiz Uyumlu Sistem (ICS)

Cramer Kuralı Sorunları Çözdü

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Yorum bırakın Yanıtı iptal et