Çizgi denklemleri -

Burada her türlü doğru denkleminin formüllerini bulacaksınız. Ayrıca bunların nasıl hesaplandığına dair örnekleri görebileceksiniz ve ayrıca doğru denklemlerinin çözülmüş alıştırmalarıyla pratik yapabileceksiniz.

Doğrunun tüm denklemleri nelerdir?

Bir çizginin matematiksel tanımının, eğriler veya açılar olmadan aynı yönde temsil edilen ardışık noktalar kümesi olduğunu unutmayın.

Bu nedenle, düzlemdeki (R2’deki) herhangi bir düz çizgiyi analitik olarak ifade etmek için düz çizginin denklemlerini kullanırız ve bunları bulmak için yalnızca düz çizgiye ait bir noktaya ve söz konusu düz çizginin yön vektörüne ihtiyacınız vardır. Yalnızca bu iki geometrik öğeyle, aşağıdaki gibi olan çizginin tüm farklı denklemlerini kesinlikle bulabilirsiniz:

Doğrunun denklemleri, vektör denklemi, parametrik denklemler, sürekli denklem, örtülü (veya genel) denklem, açık denklem, nokta-eğim denklemi ve kanonik (veya parçalı) denklemdir.

Tüm çizgi denklemi türlerinin amacı aynıdır: Bir çizgiyi matematiksel olarak temsil etmek. Ancak doğrunun her denkleminin kendine has özellikleri vardır ve bu nedenle soruna bağlı olarak birini veya diğerini kullanmak daha iyidir.

Doğru denklemleri kavramını gördükten sonra, şimdi her bir çizgi denklemi türünün özelliklerini özel olarak analiz etmeye geçiyoruz. Aşağıda satırdaki farklı denklem türlerinin ayrıntılı bir açıklaması bulunmaktadır, ancak isterseniz satırdaki tüm denklemlerin formüllerini içeren özet tablonun sonuna doğrudan gidebilirsiniz.

Doğrunun vektör denklemi

Evet

$\vv{\text{v}}$

çizginin yön vektörüdür ve

$P$

sağa ait bir nokta:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

Doğrunun vektör denkleminin formülü şöyledir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} (x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2) \end{empheq}$

Altın:

$x$

Ve

$y$

doğru üzerindeki herhangi bir noktanın Kartezyen koordinatlarıdır.
$P_1$

Ve

$P_2$

çizginin bir kısmını oluşturan bilinen bir noktanın koordinatlarıdır

$P(P}_1,P_2).$
$\text{v}_1$

Ve

$\text{v}_2$

çizginin yön vektörünün bileşenleridir

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$

değeri çizgi üzerindeki her noktaya bağlı olan bir skalerdir (gerçek sayı).

Düzlemdeki doğrunun vektör denklemidir, yani 2 koordinatlı (R2’deki) noktalar ve vektörlerle çalışırken. Ancak uzayda (R3’te) hesaplama yapıyor olsaydık, doğrunun denklemine ek bir bileşen eklemek zorunda kalırdık:

$(x,y,z)=(P_1,P_2,P_3)+t\cdot (\text{v}_1,\text{v}_2,\text{v}_3)$

Doğrunun parametrik denklemleri

Bir doğrunun parametrik denklemleri onun vektör denkleminden elde edilebilir:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

Önce parametreyi çarpıyoruz

$t$

sağın yön vektörüne göre:

$(x,y)=(P_1,P_2)+ (t\cdot\text{v}_1,t\cdot\text{v}_2)$

Daha sonra X ve Y koordinatlarını ekliyoruz:

$(x,y)=(P_1+t\cdot\text{v}_1,P_2+t\cdot\text{v}_2)$

Ve son olarak her değişkeni ayrı ayrı temizleyerek doğrunun parametrik denklemlerini elde ederiz:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases} \end{empheq}$

Altın:

$x$

Ve

$y$

doğru üzerindeki herhangi bir noktanın Kartezyen koordinatlarıdır.
$P_1$

Ve

$P_2$

çizginin bir kısmını oluşturan bilinen bir noktanın koordinatlarıdır

$P(P}_1,P_2).$
$\text{v}_1$

Ve

$\text{v}_2$

çizginin yön vektörünün bileşenleridir

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$
$t$

değeri çizgi üzerindeki her noktaya bağlı olan bir skalerdir (gerçek sayı).

Daha önce olduğu gibi, bunlar düzlemdeki (R2’deki) doğrunun parametrik denklemleridir, ancak uzaydaki (R3’teki) doğrunun parametrik denklemlerini bulmak için üçüncü değişken Z için bir denklem daha eklemek gerekli olacaktır:

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \\[1.7ex] z=P_3+t\cdot\text{v}_3\end{cases}$

Doğrunun sürekli denklemi

Herhangi bir doğrunun sürekli denklemi onun parametrik denklemlerinden çıkarılabilir:

$\displaystyle \begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

Ayarı temizlersek

$t$

her parametrik denklemden aşağıdaki ifadeleri elde ederiz:

$t =\cfrac{x-P_1}{\text{v}_1}}$

$t =\cfrac{y-P_2}{\text{v}_2}}$

E Ortaya çıkan iki denklemi eşitleyerek doğrunun sürekli denklemini elde ederiz:

$t= t$

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

Kısaca doğrunun sürekli denklemi şöyledir:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2} \end{empheq}$

Altın:

$x$

Ve

$y$

doğru üzerindeki herhangi bir noktanın Kartezyen koordinatlarıdır.
$P_1$

Ve

$P_2$

çizginin bir kısmını oluşturan bilinen bir noktanın koordinatlarıdır

$P(P}_1,P_2).$
$\text{v}_1$

Ve

$\text{v}_2$

çizginin yön vektörünün bileşenleridir

$\vv{\text{v}}=(\text{v}_1,\text{v}_2).$

Bu formül, 2 boyutlu (2 boyutlu) çalışırken çizginin sürekli denklemi içindir. Ancak 3 boyutlu (3D) işlemler yapıyor olsaydık çizgi denklemine bir bileşen daha eklememiz gerekirdi:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}= \cfrac{z-P_3}{\text{v}_3}$

Doğrunun örtülü veya genel denklemi

Evet

$\vv{\text{v}}$

çizginin yön vektörüdür ve

$P$

sağa ait bir nokta:

$\vv{\text{v}}= (\text{v}_1,\text{v}_2) \qquad P(P}_1,P_2)$

Doğrunun örtülü, genel veya Kartezyen denkleminin formülü şöyledir:

Altın:

$x$

Ve

$y$

doğru üzerindeki herhangi bir noktanın Kartezyen koordinatlarıdır.
katsayı
$A$

doğrunun yön vektörünün ikinci bileşenidir:

$A=\text{v}_2}$
katsayı
$B$

yön vektörünün ilk bileşeni değişen işarettir:

$B=-\text{v}_1}$
katsayı
$C$

bilinen nokta değiştirilerek hesaplanır

$P$

çizginin denkleminde.

Formülde, bir doğrunun örtülü denklemi, sürekli denklemin kesirleri çarpılarak da elde edilebilir.

Doğrunun açık denklemi

Doğrunun açık denkleminin formülü şöyledir:

Altın:

$m$

doğrunun eğimidir.
$n$

y-kesme noktası, yani Y ekseniyle kesiştiği yükseklik.

Aşağıdaki bölümde parametrelerin nasıl belirlendiğini göreceksiniz.

$m$

$n$

Ama özellikle açık denklemi bulmanın başka bir yolu da örtülü denklemi kullanmaktır; bunun için bilinmeyenin çözülmesi gerekiyor

$y$

örtülü denklemin.

m ve n parametrelerinin anlamı

Doğrunun açık denkleminin tanımında gördüğümüz gibi, parametre

$m$

çizginin eğimi ve

$n$

y-kesme noktası. Peki bu ne anlama geliyor? Bunu bir çizginin grafiksel gösteriminden görelim:

Bağımsız terimi

$\bm{n}$

doğrunun bilgisayar ekseni (OY ekseni) ile kesiştiği noktadır . Örneğin yukarıdaki grafikte

$n$

1’e eşittir çünkü doğru y eksenini y=1’de keser.

Öte yandan terim

$\bm{m}$

doğrunun eğimini yani eğimini gösterir . Grafikte gördüğünüz gibi,

$m$

doğru 1 yatay birim için 2 dikey birim yükseldiği için 2’ye eşittir.

Açıkçası, eğim pozitifse fonksiyon artıyor (yukarı gidiyor), diğer taraftan eğim negatifse fonksiyon azalıyor (aşağı gidiyor).

Bir çizginin eğimini hesaplayın

Bir doğrunun eğiminin tam olarak ne olduğunu öğrendikten sonra nasıl hesaplandığına bakalım. Dolayısıyla bir doğrunun eğimini sayısal olarak belirlemenin 3 farklı yolu vardır:

Doğru üzerinde iki farklı nokta verildiğinde
$P_1(x_1,y_1)$

Ve

$P_2(x_2,y_2),$

Doğrunun eğimi şuna eşittir:

$m = \cfrac{\Delta y}{\Delta x} = \cfrac{y_2-y_1}{x_2-x_1}$

Evet
$\vv{\text{v}}= (\text{v}_1,\text{v}_2)$

doğrunun yön vektörüdür, eğimi:

$m = \cfrac{\text{v}_2}{\text{v}_1}$

Evet
$\alpha$

apsis ekseni (X ekseni) ile doğrunun oluşturduğu açıdır, çizginin eğimi söz konusu açının tanjantına eşdeğerdir:

$m = \text{tg}(\alpha )$

Doğrunun nokta-eğim denklemi

Doğrunun nokta-eğim denkleminin formülü şöyledir:

Altın:

$m$

doğrunun eğimidir.
$P_1, P_2$

doğru üzerindeki bir noktanın koordinatlarıdır

$P(P_1,P_2).$

Çizginin kanonik veya segmental denklemi

Doğru denkleminin bu çeşidi daha az bilinmesine rağmen, çizginin kanonik denklemi doğrunun Kartezyen eksenlerle kesiştiği noktalardan elde edilebilir.

Belirli bir doğrunun eksenleriyle kesişen iki nokta şöyle olsun:

X ekseniyle kesin:

$(a,0)$

Y ekseniyle kesin:

$(0,b)$

Doğrunun kanonik denkleminin formülü şöyledir:

Matematikte doğrunun kanonik denklemine parçalı denklem veya simetrik denklem de denir.

Öte yandan katsayılar

$a$

$b$

Ayrıca aşağıdaki formüller kullanılarak doğrunun genel denkleminden de bulunabilirler:

$Ax+By+C=0$

$a = -\cfrac{C}{A} \qquad \qquad b = -\cfrac{C}{B}$

Doğrunun tüm denklemleri (formüller)

Özetle, doğrunun tüm denklemlerinin formüllerini gösteren bir tablo:

Doğrunun denklemlerini hesaplama örneği

Artık doğru denkleminin tüm açıklamasını gördüğümüze göre, tipik bir doğru denklemi probleminin nasıl çözüldüğüne bakalım:

Noktaya göre belirlenen doğrunun tüm denklemlerini bulun
$P$

ve vektör

$\vv{\text{v}}.$

$P(3,-1) \qquad \qquad \vv{\text{v}}=(2,4)$

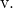
Öncelikle doğrunun vektör denklemini formülünden buluyoruz:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

Noktanın ve vektörün koordinatlarını formülde yerine koymanız yeterlidir:

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(3,-1)+t\cdot (2,4)} \quad \vphantom{\Bigl(}}$

İkinci olarak, doğrunun parametrik denklemlerini ilgili formül aracılığıyla buluyoruz:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=3+2t} \\[1.7ex] \bm{y=-1+4t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Ayrıca doğrunun sürekli denklemini de formülüyle belirliyoruz:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-3}{2}=\cfrac{y-(-1)}{4}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x-3}}{\bm{2}}\bm{=}\cfrac{\bm{y+1}}{\bm{4}}\quad \vphantom{\Biggl(}}$

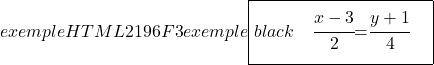
Gördüğünüz gibi vektör, parametrik ve sürekli denklemlerin hesaplanması kolaydır, sadece ilgili formüllerini kullanmanız yeterlidir.

Şimdi doğrunun genel (veya örtülü) denklemini bulmaya geçelim. Bunu yapmak için sürekli denklemin iki kesirini çaprazlıyoruz:

$4\cdot (x-3)= 2 \cdot (y+1)$

$4x-12= 2y+2$

$4x-12-2y-2=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{4x-2y-14=0}\quad \vphantom{\Bigl(}}$

Artık bilinmeyen için doğru çözümünün açık denklemini belirleyebiliriz

$y$

örtülü denklemin:

$4x-2y-14=0$

$-2y=-4x+14$

$y=\cfrac{-4x+14}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=2x-7}\quad \vphantom{\Bigl(}}$

Dolayısıyla doğrunun eğimi 2’ye (bağımsız değişkene eşlik eden terim) eşittir.

$x$

$m=2$

Ve bununla doğrunun nokta-eğim denklemini aşağıdaki formülle hesaplayabiliriz:

$y-P_2=m(x-P_1)$

$y-(-1)=2(x-3)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y+1=2(x-3)}\quad \vphantom{\Bigl(}}$

Son olarak doğrunun bölümsel denklemini bulmak için çizginin OX ve OY eksenleriyle kesişme noktalarını hesaplıyoruz ve ardından formülünü uyguluyoruz:

$y=2x-7$

Apsis ekseni (X ekseni) ile kesişme noktası

$y=0$

$0=2x-7$

$-2x=-7$

$x=\cfrac{-7}{-2} = \cfrac{7}{2}$

$\displaystyle \left(\frac{7}{2}, 0\right)$

Y ekseni (Y ekseni) ile kesişme noktası

$x=0$

$y=2\cdot 0-7$

$y=-7$

$\displaystyle \left(0,-7\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\frac{\bm{7}}{\bm{2}}}+\cfrac{\bm{y}}{\bm{-7}} \bm{= 1} \quad \vphantom{\Biggl(}}$

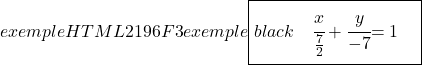
iki noktadan geçen doğru denklemi

Doğru denklemlerinde çok sık karşılaşılan bir diğer problem ise verilen iki nokta tarafından belirlenen doğrunun denklemini bulmaktır. Her ne kadar 2 nokta ve ardından denklem ile doğrunun yön vektörünü hesaplayabilsek de, aşağıda söz konusu doğrunun denklemini doğrudan ve kolayca bulabileceğiniz bir formül sunuyoruz.

Bir çizgi üzerinde bulunan iki noktayı düşünün:

$P_1(x_1,y_1) \qquad \qquad P_2(x_2,y_2)$

Doğrunun denklemini 2 noktasından bulma formülü :

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1) \end{empheq}$

Bu formül bize doğrunun geçtiği 2 nokta verildiğinde doğrunun nokta-eğim denklemini doğrudan hesaplamamızı sağlar.

Doğru denklemlerinin çözülmüş problemleri

1. Egzersiz

Noktayla tanımlanan doğrunun vektör denklemini, parametrik denklemlerini ve sürekli denklemini bulun

$P$

ve onun yönlendirici vektörü

$\vv{\text{v}}.$

Her ikisi de olun:

$P(0,3) \qquad \qquad \vv{\text{v}}=(-1,5)$

Çözüme bakın

Öncelikle doğrunun vektör denklemini formülünden hesaplıyoruz:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(0,3)+t\cdot (-1,5)} \quad \vphantom{\Bigl(}}$

Daha sonra ilgili formülü kullanarak doğrunun parametrik denklemlerini buluruz:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\begin{cases} x=0+t\cdot (-1) \\[1.7ex] y=3+t\cdot 5\end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-t} \\[1.7ex] \bm{y=3+5t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Ve son olarak doğrunun sürekli denklemini ilgili formülüyle belirliyoruz:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-0}{-1}=\cfrac{y-3}{5}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x}}{\bm{-1}}\bm{=}\cfrac{\bm{y-3}}{\bm{5}}\quad \vphantom{\Biggl(}}$

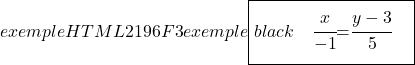
Alıştırma 2

Noktaya göre belirlenen doğrunun örtülü denklemini, açık denklemini ve nokta-eğim denklemini bulun

$P$

ve yön vektörü

$\vv{\text{v}}.$

$P(-4,3) \qquad \qquad \vv{\text{v}}=(2,6)$

Çözüme bakın

Doğrunun örtülü denkleminin formülü şöyledir:

$Ax+By+C=0$

Bu nedenle A, B ve C katsayılarını bulmalıyız. A ve B bilinmeyenleri çizginin yön vektörünün koordinatlarından elde edilir, çünkü aşağıdaki eşitlik her zaman doğrulanır:

$\vv{\text{v}}= (-B,A)$

Sonuç olarak, A katsayısı vektörün ikinci koordinatıdır ve B katsayısı vektör değişen işaretin ilk koordinatıdır:

$\left.\begin{array}{c}\vv{\text{v}}= (-B,A) \\[2ex] \vv{\text{v}}= (2,6) \end{array} \right\}\longrightarrow \begin{array}{l}A=6 \\[2ex] B=-2 \end{array}$

Bu nedenle sadece C katsayısını bulmamız gerekiyor. Bunun için doğruya ait olduğunu bildiğimiz noktayı denklemde yerine koymalıyız:

$P(-4,3)$

$6x-2y+C=0 \ \xrightarrow{x=-4 \ ; \ y=3} \ 6\cdot (-4)-2\cdot 3+C=0$

$-24-6+C=0$

$-30+C=0$

$C=30$

Dolayısıyla doğrunun örtülü, genel veya Kartezyen denklemi şöyledir:

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x-2y+30=0}\quad \vphantom{\Bigl(}}$

Artık bilinmeyen için doğru çözümünün açık denklemini belirleyebiliriz

$y$

örtülü denklemin:

$6x-2y+30=0$

$-2y=-6x-30$

$y=\cfrac{-6x-30}{-2}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=3x+15}\quad \vphantom{\Bigl(}}$

Bu nedenle doğrunun eğimi 3’e eşittir (bağımsız değişkenden önceki terim)

$x$

$m=3$

Ve çizginin eğiminin değerinden çizginin nokta-eğim denklemini aşağıdaki formülle hesaplayabiliriz:

$y-P_2=m(x-P_1)$

$y-3=3(x-(-4))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-3=3(x+4)}\quad \vphantom{\Bigl(}}$

Alıştırma 3

Aşağıdaki doğru üzerinde örtülü veya genel bir denklem olarak ifade edilen 3 noktayı belirleyin:

$4x+2y-8 = 0$

Çözüme bakın

Bir doğru üzerindeki bir noktayı hesaplamak için değişkenlerden birine bir değer atamamız ve ardından diğer değişkenin o noktadaki değerini bulmamız yeterlidir.

Bunu yaparak bir ilk noktayı hesaplıyoruz

$x=0:$

$4\cdot 0+2y-8 = 0$

$2y = 8$

$y = \cfrac{8}{2}$

$y = 4$

$\bm{P_1(0,4)}$

Daha sonra değişkene başka bir değer veren ikinci bir nokta buluyoruz

$x,$

Örneğin

$x=1:$

$4\cdot 1+2y-8 = 0$

$2y = 8-4$

$2y = 4$

$y = \cfrac{4}{2}$

$y = 2$

$\bm{P_2(1,2)}$

Ve son olarak üçüncü noktayı çözerek hesaplıyoruz.

$x=2:$

$4\cdot 2+2y-8 = 0$

$2y = 8-8$

$2y = 0$

$y = \cfrac{0}{2}$

$y = 0$

$\bm{P_3(2,0)}$

Alıştırma 4

Noktayla tanımlanan çizginin tüm denklemlerini bulun

$P$

ve vektör

$\vv{\text{v}}.$

$P(-1,4) \qquad \qquad \vv{\text{v}}=(-3,6)$

çözümü gör

Öncelikle doğrunun vektör denklemini formülünden buluyoruz:

$(x,y)=(P_1,P_2)+t\cdot (\text{v}_1,\text{v}_2)$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{(x,y)=(-1,4)+t\cdot (-3,6)} \quad \vphantom{\Bigl(}}$

İkinci olarak, doğrunun parametrik denklemlerini ilgili formül aracılığıyla buluyoruz:

$\begin{cases} x=P_1+t\cdot\text{v}_1 \\[1.7ex] y=P_2+t\cdot\text{v}_2 \end{cases}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \begin{cases} \bm{x=-1-3t} \\[1.7ex] \bm{y=4+6t} \end{cases} \quad \vphantom{\cfrac{\cfrac{1}{2}}{\cfrac{1}{2}}} }$

Ayrıca formülünü kullanarak çizginin sürekli denklemini de belirliyoruz:

$\cfrac{x-P_1}{\text{v}_1}=\cfrac{y-P_2}{\text{v}_2}$

$\cfrac{x-(-1)}{-3}=\cfrac{y-4}{6}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \cfrac{\bm{x+1}}{\bm{-3}}\bm{=}\cfrac{\bm{y-4}}{\bm{6}}\quad \vphantom{\Biggl(}}$

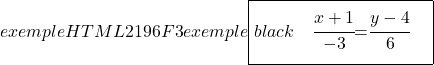
Şimdi doğrunun örtülü veya genel denklemini bulmaya geçelim. Bunu yapmak için sürekli denklemin iki kesirini çaprazlıyoruz:

$6\cdot (x+1)= -3 \cdot (y-4)$

$6x+6= -3y+12$

$6x+6+3y-12=0$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{6x+3y-6=0}\quad \vphantom{\Bigl(}}$

Artık bilinmeyen için doğru çözümünün açık denklemini belirleyebiliriz

$y$

örtülü denklemin:

$6x+3y-6=0$

$3y=-6x+6$

$y=\cfrac{-6x+6}{3}$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad \bm{y=-2x+2}\quad \vphantom{\Bigl(}}$

Bu nedenle doğrunun eğimi -2’ye (bağımsız değişkene eşlik eden terim) eşdeğerdir.

$x$

$m=-2$

Ve bununla doğrunun nokta-eğim denklemini aşağıdaki formülle hesaplayabiliriz:

$y-P_2=m(x-P_1)$

$y-4=-2(x-(-1))$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\bm{y-4=-2(x+1)}\quad \vphantom{\Bigl(}}$

Son olarak doğrunun segmental denklemini bulmak için doğrunun OX ve OY eksenleriyle kesişme noktalarını hesaplıyoruz ve ardından formülünü kullanıyoruz:

$y=-2x+2$

Apsis ekseni (X ekseni) ile kesişme noktası

$y=0$

$0=-2x+2$

$2x=2$

$x=\cfrac{2}{2} =1$

$\displaystyle \left(1, 0\right)$

Y ekseni (Y ekseni) ile kesişme noktası

$x=0$

$y=-2\cdot 0+2$

$y=2$

$\displaystyle \left(0,2\right)$

$\cfrac{x}{a}+\cfrac{y}{b} = 1$

$\definecolor{exemple}{HTML}{2196F3} \color{exemple} \boxed{ \color{black} \quad\cfrac{\bm{x}}{\bm{1}}+\cfrac{\bm{y}}{\bm{2}} \bm{= 1} \quad \vphantom{\Biggl(}}$

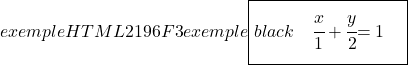
Alıştırma 5

Aşağıdaki iki noktadan geçen doğrunun denklemini bulunuz:

$P_1 (4,-1) \qquad \qquad P_2(5,2)$

çözümü gör

Doğru üzerindeki iki noktayı zaten bildiğimiz için, doğrunun denklem formülünü verilen 2 noktaya doğrudan uyguluyoruz:

$y-y_1= \cfrac{y_2-y_1}{x_2-x_1} (x-x_1)$

Şimdi noktaların Kartezyen koordinatlarını formülde yerine koyuyoruz:

$y-(-1)= \cfrac{2-(-1)}{5-4} (x-4)$

Ve son olarak doğrunun eğimini hesaplıyoruz:

$y+1= \cfrac{3}{1} (x-4)$

$y+1= 3(x-4)$

Bu iki noktadan geçen doğrunun denklemi şu şekildedir:

$\bm{y+1= 3(x-4)}$

Doğrunun tüm denklemleri nelerdir?

Doğrunun vektör denklemi

Doğrunun parametrik denklemleri

Doğrunun sürekli denklemi

Doğrunun örtülü veya genel denklemi

Doğrunun açık denklemi

m ve n parametrelerinin anlamı

Bir çizginin eğimini hesaplayın

Doğrunun nokta-eğim denklemi

Çizginin kanonik veya segmental denklemi

Doğrunun tüm denklemleri (formüller)

Doğrunun denklemlerini hesaplama örneği

iki noktadan geçen doğru denklemi

Doğru denklemlerinin çözülmüş problemleri

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Yorum bırakın Yanıtı iptal et