Bu sayfada boş matris olarak da adlandırılan sıfır matrisinin açıklamasını bulacaksınız. Ayrıca elemanlarının değerlerinin matrisin boyutundan bağımsız olduğunu örneklerle görecek ve sonunda bu tip matrislerin tüm özelliklerini bulacaksınız.
Sıfır matrisi nedir?
Boş matris (veya boş matris), elemanlarının tümü sıfıra (0) eşit olan bir matristir.
Dolayısıyla sıfır matrisin tanımı gereği bu matris, tüm sayıları sıfır olduğu sürece mümkün olan tüm boyutlarda olabilir. Aşağıdaki örneklere bakın:
Boş matris örnekleri
2 × 2 boş matris örneği
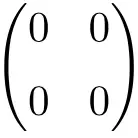
3 × 3 boş matris örneği
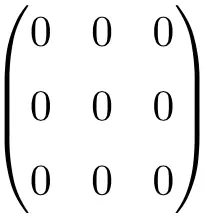
4 × 4 boş matris örneği
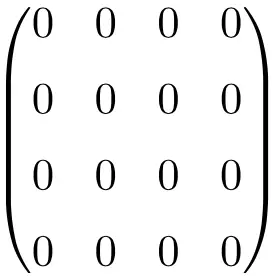
Şimdi size bu çok özel matrisin hiçbir önemi yokmuş gibi görünebilir, çünkü bu sadece sıfırlarla dolu bir matristir. Ancak matematikte, özellikle de lineer cebir alanında, hesaplamaları çok daha kolay hale getirdiği için çok kullanışlı bir matristir.
Boş matrisin özellikleri
Boş (veya boş) matrisler aşağıdaki özelliklere sahiptir:
- Sıfır matris, matris toplama işleminin nötr elemanıdır, dolayısıyla:
![]()
- Matris çarpımı sıfırın çarpımsal özelliğine sahiptir, yani herhangi bir matrisin sıfır matrisi ile çarpımı 0’a eşittir.
![]()
- Matris kare ise sıfır matrisi hem simetrik hem de antisimetriktir .
- Sıfır matrisi, derecesi sıfır olan tek matristir.
- Sıfır matrisinin determinantı her zaman 0 olarak değerlendirilir, dolayısıyla bu tür bir matrisin tersi yoktur (tekil bir matristir).
- Açıkçası, sıfır matrisi üstelsıfır matrisin bir örneğidir .