Bir vektörün modülü nasıl hesaplanır

Bu sayfada bir vektörün büyüklüğünün açıklamasını ve formülüyle nasıl hesaplanacağını göreceksiniz. Ayrıca modülü iki noktadan nasıl bulacağınızı görebileceksiniz: kökeni ve sonu. Ek olarak, bir vektörün bileşenlerini, modülünden ve bir vektörün modülünün özelliklerinden nasıl belirleyeceğinizi keşfedeceksiniz. Hatta örneklerle, alıştırmalarla ve adım adım problemlerle pratik yapabilirsiniz.

Bir vektörün modülü nedir?

Bir vektörün büyüklüğü, başlangıç noktası ile sonu arasındaki mesafeyi temsil eder. Dolayısıyla bir vektörün büyüklüğü söz konusu vektörün uzunluğuna eşittir.

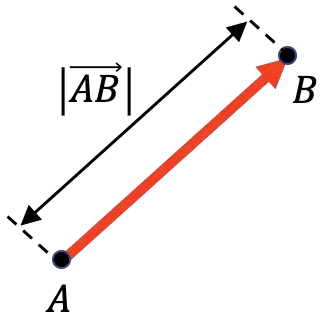
Yukarıdaki grafiksel gösterimde görebileceğiniz gibi, bir vektörün büyüklüğü, vektörün her iki yanında bulunan dikey bir çubukla sembolize edilir:

$\lvert \vv{AB}\rvert$

Öte yandan, bir vektörün modülü bir vektörün normuyla aynıdır, dolayısıyla bu şekilde yazıldığını da görebilirsiniz. Bu nedenle bir vektörün modülünü her iki tarafta iki dikey çubukla temsil eden matematikçiler vardır:

$\lvert \lvert \vv{AB}\rvert\rvert$

Bir vektörün modülü için formül

Düzlemdeki bir vektörün büyüklüğünü bulmak için aşağıdaki formülü uygulamamız gerekir:

Bir vektörün büyüklüğünü belirlemek için, bileşenlerinin kareleri toplamının (pozitif) karekökünü hesaplamamız gerekir. Başka bir deyişle, eğer aşağıdaki vektöre sahipsek:

$\vv{\text{u}} = (\text{u}_x,\text{u}_y)$

Modülü:

$\displaystyle \lvert \vv{\text{u}} \rvert = \sqrt{ \text{u}_x^2+\text{u}_y^2}$

Örneğin aşağıdaki vektörün büyüklüğünü aşağıdaki formülü kullanarak hesaplayacağız:

$\vv{\text{u}} = (4,3)$

$\lvert \vv{\text{u}} \rvert =\sqrt{4^2+3^2} = \sqrt{16+9}=\sqrt{25} = \bm{5}$

Bir vektörün büyüklüğünü başlangıç ve bitiş koordinatlarıyla hesaplayın

Bir vektörün büyüklüğünün, bileşenlerini bildiğimizde nasıl belirlendiğini gördük, peki sadece başladığı ve bittiği noktaları bilseydik ne olurdu?

Bu nedenle, bir vektörün büyüklüğünü başlangıç ve bitiş koordinatlarından hesaplamak için şu iki adımı izlemelisiniz:

Önce vektörün bileşenlerini buluyoruz. Bunu yapmak için ekstremum eksi orijini çıkarmamız gerekir.
Daha sonra bir önceki bölümde gördüğümüz formülle elde edilen vektörün modülünü hesaplıyoruz.

Bunun nasıl yapıldığını bir örnek üzerinden görelim:

Kökeni nokta olan vektörün büyüklüğünü hesaplayın
$A(2,1)$

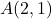
ve son nokta olarak

$B(-1,4).$

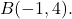
Öncelikle vektörün bileşenlerini bulmamız gerekiyor, dolayısıyla uç noktasından kökenini çıkarıyoruz:

$\vv{AB}=B-A=(-1,4)-(2,1)=(-3,3)$

Vektörü bildiğimizde, vektör büyüklüğü formülünü kullanarak büyüklüğünü hesaplarız:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{(-3)^2+3^2} = \sqrt{9+9}=\sqrt{18}$

Ve sonucu karekök olarak bırakıyoruz çünkü kesin değil.

Bir vektörün bileşenleri modülünden nasıl hesaplanır

Bir vektörün büyüklüğünü bileşenlerinden nasıl çıkaracağımızı gördük, ancak süreç tersine de çevrilebilir. Başka bir deyişle, bir vektörün bileşenlerini modülü aracılığıyla hesaplayabiliriz.

Bir vektörün bileşenlerini büyüklüğünden bulma işlemine vektör ayrıştırması denir. Dolayısıyla, bir vektörü ayrıştırmak için onun büyüklüğüne ve apsis ekseni (X ekseni) ile oluşturduğu açıya ihtiyacımız var.

Böylece vektörün X ve Y bileşenleri trigonometrik oranlarla hesaplanabilir:

Resimde görebileceğiniz gibi, bir vektörün büyüklüğü bileşenleriyle birlikte bir dik üçgen oluşturur, böylece trigonometrinin temel formülleri uygulanabilir.

Bir vektörün modülünden farklı olarak, sinüs ve kosinüsün negatif değerler alabilmesi nedeniyle bileşenlerinin negatif olabileceği dikkate alınmalıdır.

Örnek olarak, büyüklüğü ve OX ekseni ile açısı olan vektörün vektör ayrışımı:

$\lvert \vv{\text{u}} \rvert = 10 \qquad \alpha = 60º$

Vektörün yatay bileşeni, modül ile açının kosinüsünün çarpımına eşittir:

$\text{u}_x= \lvert \vv{\text{u}}\rvert \cdot \text{cos}(60º)= 10 \cdot 0,5 = 5$

Ve vektörün dikey bileşeni, modülü açının sinüsüyle çarpmaya eşittir:

$\text{u}_y= \lvert \vv{\text{u}}\rvert \cdot \text{sen}(60º)= 10 \cdot 0,87 = 8,7$

Yani vektör aşağıdaki gibidir:

$\vv{\mathbf{u}}\bm{ = (5 \ ,\ 8,7)}$

Bir vektörün modül özellikleri

Modül, aşağıdaki özelliklere sahip bir vektör işlemi türüdür:

Bir vektörün büyüklüğü hiçbir zaman negatif olamaz , her zaman 0’a eşit veya 0’dan büyük olacaktır.

$\lvert \vv{\text{u}} \rvert \geq 0$

Aslında sıfır büyüklükte var olan tek vektör sıfır vektördür, yani vektör

$\vv{\text{u}}= (0,0) .$

Bir vektörün gerçek bir sayıyla (veya bir skalerle) çarpımının büyüklüğü, skalerin mutlak değerinin vektörün büyüklüğüyle çarpılmasına eşdeğerdir. Bu nedenle aşağıdaki eşitlik geçerlidir:

$\lvert k \cdot \vv{\text{u}} \rvert = \lvert k \rvert \cdot \lvert \vv{\text{u}} \rvert$

Üçgen eşitsizliği doğrulandı: iki vektörün toplamının modülü, ayrı ayrı modüllerinin toplamından küçük veya ona eşit.

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert \leq \lvert\vv{\text{u}} \rvert+\lvert\vv{\text{v}} \rvert$

Ek olarak, iki vektörün toplamının büyüklüğü aşağıdaki denklemle nokta çarpımla ilişkilidir:

$\lvert \vv{\text{u}}+\vv{\text{v}} \rvert = \sqrt{\lvert \vv{\text{u}} \rvert ^2+\lvert \vv{\text{v}} \rvert ^2 +2\cdot \vv{\text{u}}\cdot \vv{\text{v}} \vphantom{\sqrt{x^2}}}$

birim vektör

Matematikte birim vektör , modülü bire eşit olan bir vektördür.

$\lvert \vv{\text{u}} \rvert=1$

Bu nedenle birim vektörün uzunluğu bir birimdir.

Bir vektörün modülünün tam olarak 1 olması çok zor görünebilir, ancak bu tür bir vektörü bulmak aslında kolaydır:

Herhangi bir vektörün birim vektörünü bulmak için onu modülüne bölmeniz yeterlidir:

$\vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert}$

Altın

$\vv{\text{v}}_u$

birim vektörüdür

$\vv{\text{v}},$

$\lvert \vv{\text{v}} \rvert$

sizin modülünüz.

Birim vektöre versor veya normalleştirilmiş vektör de denir.

Ek olarak birim vektör, orijinal vektörle aynı yön ve yöne sahiptir.

Örneğin aşağıdaki vektörün birim vektörünü hesaplayacağız:

$\vv{\text{v}}=(1,-1)$

Vektörü normalleştirmek için önce büyüklüğünü hesaplamamız gerekir:

$\lvert \vv{\text{v}} \rvert=\sqrt{1^2+(-1)^2} = \sqrt{2}$

Ve son olarak, orijinal vektörü modülüne bölerek birim vektörü hesaplıyoruz:

$\displaystyle \vv{\text{v}}_u = \cfrac{\vv{\text{v}}}{\lvert \vv{\text{v}} \rvert} = \frac{(1,-1)}{\sqrt{2}}= \bm{\left(\frac{1}{\sqrt{2}},-\frac{1}{\sqrt{2}} \right)}$

Çözülmüş vektör modülü alıştırmaları

1. Egzersiz

Aşağıdaki vektörün büyüklüğünü hesaplayın:

$\vv{a}=(6,8)$

Çözüme bakın

Vektörün modülünü hesaplamak için formülünü uygulamalıyız:

$\lvert\vv{a} \rvert= \sqrt{6^2+8^2} =\sqrt{36+64} = \sqrt{100} = \bm{10}$

Alıştırma 2

Aşağıdaki vektörleri en kısadan en uzuna doğru sıralayınız.

$\vv{a}=(4,-2)$

$\vv{b}=(3,1)$

$\vv{c}=(5,12)$

$\vv{d}=(-6,-3)$

Çözüme bakın

Bir vektörün uzunluğu büyüklüğüne eşittir. Bu nedenle tüm vektörlerin modüllerini hesaplamamız gerekiyor:

$\left|\vv{a}\right|= \sqrt{4^2+(-2)^2} =\sqrt{16+4} = \sqrt{20}$

$|\vv{b}|= \sqrt{3^2+1^2} =\sqrt{9+1} = \sqrt{10}$

$\begin{vmatrix}\vv{c}\end{vmatrix}= \sqrt{5^2+12^2} =\sqrt{25+144} = \sqrt{169} = 13$

$|\vv{d}| = \sqrt{(-6)^2+(-3)^2} =\sqrt{36+9} = \sqrt{45}$

Böylece, en küçükten en büyük uzunluğa (veya modüle) doğru sıralanan vektörler şöyledir:

$|\vv{b}|< \begin{vmatrix}\vv{a}\end{vmatrix} < |\vv{d}| < \begin{vmatrix}\vv{c}\end{vmatrix}$

Alıştırma 3

Kökeni nokta olan vektörün büyüklüğünü belirleyin

$A(-3,2)$

ve son nokta olarak

$B(7,-4).$

çözümü gör

Modülünü hesaplamak için önce vektörü bulmalısınız. Bunu yapmak için ekstremum eksi orijini çıkarırız:

$\vv{AB}=B-A=(7,-4)-(-3,2)=(10,-6)$

Vektörü bildiğimizde modülü, modül formülü kullanılarak hesaplanır:

$\begin{vmatrix} \vv{AB} \end{vmatrix} =\sqrt{10^2+(-6)^2} = \sqrt{100+36}=\bm{\sqrt{136}}$

Alıştırma 4

Aşağıdaki vektörü ayrıştırın ve bileşenlerini bulun:

$\lvert \vv{a} \rvert =8 \qquad \alpha = 45º$

çözümü gör

Vektörün yatay bileşeni, modül ile açının kosinüsünün çarpımına eşittir:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(45º)= 8 \cdot 0,71 = 5,66$

Ve vektörün dikey bileşeni, modülü açının sinüsüyle çarpmaya eşittir:

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(45º)= 8 \cdot 0,71 = 5,66$

Yani vektör aşağıdaki gibidir:

$\vv{\mathbf{u}}\bm{ = (5,66 \ ,\ 5,66)}$

Bu durumda iki bileşen aynıdır, yani vektörün eğim açısı 45°’dir.

Alıştırma 5

Vektörü, aşağıdaki vektörle aynı yön ve doğrultuda, ancak modül 1 ile hesaplayın.

$\vv{a} = (-4,3)$

çözümü gör

Aynı yönde ve aynı yönde ancak modül 1’e sahip vektör birim vektördür. Bunu hesaplamak için önce vektörün modülünü buluyoruz:

$\lvert \vv{a} \rvert=\sqrt{(-4)^2+3^2} = \sqrt{16+9} = \sqrt{25} = 5$

Şimdi orijinal vektörü modülüne bölerek birim vektörü hesaplıyoruz:

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(-4,3)}{5}= \bm{\left(-\frac{4}{5},\frac{3}{5} \right)}$

Alıştırma 6

Aşağıdaki vektörü vektörel olarak ayrıştırın ve birim vektörünü hesaplayın:

$\lvert \vv{a} \rvert =6 \qquad \alpha = 20º$

çözümü gör

İlk önce vektörü ayrıştırıyoruz ve koordinatlarını buluyoruz:

$a_x= \lvert \vv{a}\rvert \cdot \text{cos}(20º)= 6 \cdot 0,94 = 5,64$

$a_y= \lvert \vv{a}\rvert \cdot \text{sen}(20º)= 6 \cdot 0,34 = 2,05$

Yani vektör aşağıdaki gibidir:

$\vv{a}= (5,64 \ ,\ 2,05)}$

Şimdi birim vektörü, elde edilen vektörü modülüne bölerek hesaplıyoruz:

$\displaystyle \vv{a}_u = \cfrac{\vv{a}}{\lvert \vv{a} \rvert} = \frac{(5,64 \ ,\ 2,05)}{6}= \bm{(0,94 \ , \ 0,34) }$

Birim vektörün bileşenlerinin, X ekseniyle oluşturduğu açının kosinüs ve sinüsüne eşit olduğuna dikkat edin.

Bir vektörün modülü nedir?

Bir vektörün modülü için formül

Bir vektörün büyüklüğünü başlangıç ve bitiş koordinatlarıyla hesaplayın

Bir vektörün bileşenleri modülünden nasıl hesaplanır

Bir vektörün modül özellikleri

birim vektör

Çözülmüş vektör modülü alıştırmaları

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Alıştırma 5

Alıştırma 6

Yorum bırakın Yanıtı iptal et