Bu sayfada bir segmentin orta noktasının anlamı açıklanmaktadır. Ayrıca formülünü kullanarak bir parçanın ortasını nasıl bulacağınızı da öğreneceksiniz. Hatta segment orta noktalarına ilişkin örnekleri, alıştırmaları ve çözülmüş sorunları göreceksiniz.
Bir segmentin orta noktası nedir?
Matematikte bir parçanın orta noktası , parçanın uç noktalarına aynı mesafede bulunan noktadır. Bu nedenle orta, segmenti iki eşit parçaya böler.
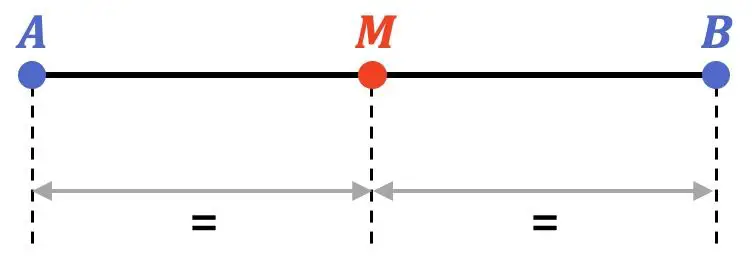
Ayrıca orta nokta doğru parçasının tam ortasında olduğundan doğru parçasının açıortayına aittir.
Öte yandan, bir doğru parçasının orta noktası aynı zamanda iki geometrik unsurdan da eşit uzaklıkta olan bir noktadır: doğru parçasının iki ucu.
Bir segmentin orta noktası nasıl hesaplanır?
Bir parçanın uç noktalarının Kartezyen koordinatları göz önüne alındığında:
![]()
Söz konusu parçanın ortasının koordinatları, uç noktaların koordinatlarının yarı toplamına karşılık gelir:
![]()
Bu, Kartezyen düzlemdeki (R2’deki) bir parçanın ortasının formülüdür. Ancak formülün Kartezyen uzaya (R3’te) de uygulanabileceği açıktır, sadece Z koordinatının yarım toplamını eklemeniz gerekir:
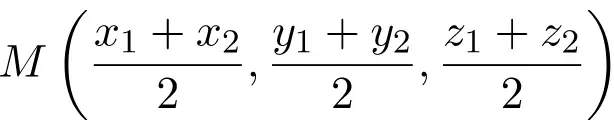
Bir parçanın orta noktasının koordinatlarının nasıl hesaplanacağına dair bir örneğe bakalım:
- Aşağıdaki noktaların oluşturduğu doğru parçasının orta noktasını belirleyin:
![]()
Segmentin ortasını bulmak için formülünü uygulamanız yeterlidir:
![]()
![]()
![]()
![]()
Bir bölümün ortasında çözülen alıştırmalar
1. Egzersiz
Uç noktaları aşağıdaki iki nokta olan doğru parçasının orta noktası nedir?
![]()
Segmentin ortasını bulmak için doğrudan formülü uygulamanız gerekir:
![]()
![]()
![]()
![]()
Alıştırma 2
A noktasında başlayan ve orta noktası M olan doğru parçasının bitiş noktasının koordinatlarını bulun.
![]()
Bu durumda başlangıç noktasının ve parçanın ortasının koordinatlarını biliyoruz. Bu nedenle bildiğimiz koordinatları bir doğru parçasının orta noktası formülünde yerine koyarız:
![]()
![]()
Şimdi önceki denklemden parçanın bitiş noktasının koordinatlarını çözüyoruz:
X koordinatları
![]()
![]()
![]()
![]()
![]()
Y koordinatları
![]()
![]()
![]()
![]()
![]()
Bu nedenle segmentin son ucunun koordinatları şöyledir:
![]()
Alıştırma 3
Aşağıdaki paralelkenar göz önüne alındığında:
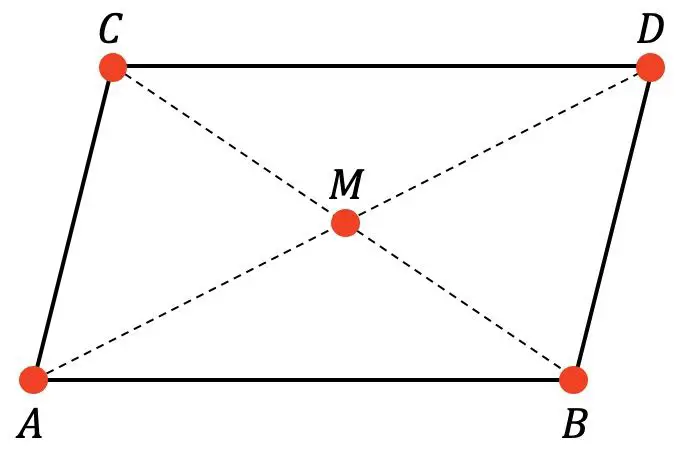
M’nin paralelkenarın merkezi olduğunu ve A, B ve C noktalarının koordinatlarının şöyle olduğunu biliyoruz:
![]()
Bu bilgiye dayanarak ve orta nokta formülünü kullanarak D noktasının koordinatlarını hesaplayın.
Bir doğru parçasının ortası formülünü kullanarak D noktasının koordinatlarını bulmak için önce M noktasının koordinatlarını, ardından D noktasının koordinatlarını hesaplamanız gerekir.
M noktası BC doğru parçasının orta noktasıdır, dolayısıyla koordinatları şöyledir:
![]()
![]()
M noktasını bildiğimizde D noktasını bulabiliriz. M noktası aynı zamanda AD doğru parçasının da ortasıdır, yani:
![]()
D noktasının X koordinatı
![]()
![]()
![]()
D noktasının Y koordinatı
![]()
![]()
![]()
Dolayısıyla D noktasının koordinatları şöyledir:
![]()
Alıştırma 4
Orta noktasında PQ segmentine dik olan doğrunun sürekli denklemini hesaplayın. Noktalar olun
![]()
Ve
![]()
Bir doğrunun denklemini belirlemek için onun yön vektörüne ve doğrunun parçası olan bir noktaya ihtiyacımız var.
Bu durumda doğrunun yön vektörü vektöre dik olacaktır.
![]()
Bu nedenle vektörü hesaplıyoruz
![]()
![]()
Ve vektörün bileşenlerini aralarında değiştirerek ve ardından bir bileşenin işaretini değiştirerek diğerine dik bir vektör bulabiliriz , dolayısıyla:
![]()
Artık doğrunun yön vektörüne sahibiz, dolayısıyla doğruya ait yalnızca bir noktaya ihtiyacımız var. Bu durumda talimat bize doğrunun parçanın orta noktasından geçtiğini söyler, bu nedenle orta noktayı aşağıdaki formülü kullanarak hesaplarız:
![]()
![]()
Son olarak hesaplanan nokta ve vektörden doğrunun sürekli denklemini oluşturuyoruz:
![]()