Bir sayının bir matrisle çarpımı

Bu sayfada bir sayıyı bir matrisle nasıl çarpacağımızı göreceğiz. Ayrıca mükemmel bir şekilde anlamanıza yardımcı olacak örnekler ve pratik yapabilmeniz için çözülmüş alıştırmalar da var. Ayrıca bir skaler ve bir matrisin çarpımının tüm özelliklerini bulacaksınız.

Bir sayı bir matrisle nasıl çarpılır?

Bir sayıyı bir matrisle çarpmak için matrisin her elemanını sayıyla çarpın.

Örnek:

bir sayının bir matrisle çarpımı veya çarpımı örneği

Bir sayıyı bir matrisle çarpmayla ilgili çözülmüş problemler

1. Egzersiz:

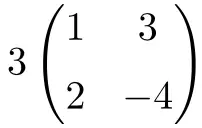
Bir sayının 2x2'lik bir matrisle çarpımının alıştırması, matrislerle işlemler

Çözüme bakın

Bir skalerin 2. dereceden bir kare matrisle çarpımıdır:

$\displaystyle 3 \begin{pmatrix} 1 & 3 \\[1.1ex] 2 & -4 \end{pmatrix} = \begin{pmatrix} 3\cdot 1 & 3\cdot 3 \\[1.1ex] 3\cdot 2 & 3\cdot (-4) \end{pmatrix} = \begin{pmatrix} \bm{3} & \bm{9} \\[1.1ex] \bm{6} & \bm{-12} \end{pmatrix}$

Egzersiz 2:

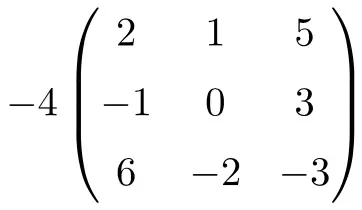
bir sayının 3x3'lük bir matrisle çarpımı, matrislerle işlemler adım adım çözüldü

Çözüme bakın

Bir sayının 3. dereceden bir kare matrisle çarpımıdır:

$\displaystyle -4 \begin{pmatrix} 2 & 1 & 5 \\[1.1ex] -1 & 0 & 3 \\[1.1ex] 6 & -2 & -3 \end{pmatrix} = \begin{pmatrix} -4 \cdot 2 & -4 \cdot 1 & -4 \cdot 5 \\[1.1ex] -4 \cdot (-1) & -4 \cdot 0 & -4 \cdot 3 \\[1.1ex] -4 \cdot 6 & -4 \cdot (-2) & -4 \cdot (-3) \end{pmatrix}= \begin{pmatrix} \bm{-8} & \bm{-4} & \bm{-20} \\[1.1ex] \bm{4} & \bm{0} & \bm {-12} \\[1.1ex] \bm{-24} & \bm{8} & \bm {12} \end{pmatrix}$

Egzersiz 3:

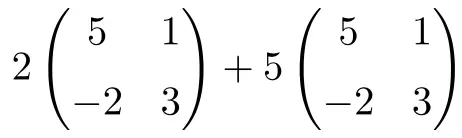
Bir sayının 2x2'lik bir matrisle çarpımına ilişkin çözülmüş alıştırma, matrislerle birleştirilmiş işlemler

Çözüme bakın

Sayıların matrislerle çarpımını ve 2×2 boyutlu matrislerin toplamlarını birleştiren bir işlemdir:

$\displaystyle 2 \begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}+5\begin{pmatrix} 5 & 1 \\[1.1ex] -2 & 3 \end{pmatrix}$

Bu nedenle öncelikle çarpımları çözmemiz gerekiyor:

$\displaystyle \begin{pmatrix} 10 & 2 \\[1.1ex] -4 & 6 \end{pmatrix}+\begin{pmatrix} 25 & 5 \\[1.1ex] -10 & 15 \end{pmatrix}$

Ve son olarak elde edilen matrisleri ekliyoruz:

$\displaystyle \begin{pmatrix} \bm{35} & \bm{7} \\[1.1ex] \bm{-14} & \bm{21} \end{pmatrix}$

Egzersiz 4:

Aşağıdaki matrisleri göz önünde bulundurun:

$\displaystyle A=\begin{pmatrix} 2 & -3 & 5 \\ 1 & 4 & 0 \\ -3 & 2 & -5 \end{pmatrix} \qquad B=\begin{pmatrix} 6 & 0 & 2 \\ -3 & 4 & 1 \\ 3 & 2 & 7 \end{pmatrix}$

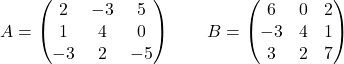
Hesaplamak:

$\displaystyle -2A+5I-3B$

Çözüme bakın

Skaler çarpımları 3×3 boyutlu matrislerin toplama ve çıkarma işlemleriyle birleştiren bir işlemdir. Ayrıca matris

$I$

ana köşegende 1 ve geri kalan elemanlarda 0’dan oluşan birim matristir:

$\displaystyle -2\begin{pmatrix} 2 & -3 & 5 \\[1.1ex] 1 & 4 & 0 \\[1.1ex] -3 & 2 & -5 \end{pmatrix}+5\begin{pmatrix} 1 & 0 & 0 \\[1.1ex] 0 & 1 & 0 \\[1.1ex] 0 & 0 & 1 \end{pmatrix} -3 \begin{pmatrix} 6 & 0 & 2 \\[1.1ex] -3 & 4 & 1 \\[1.1ex] 3 & 2 & 7 \end{pmatrix}$

Bu nedenle öncelikle çarpma işlemlerini gerçekleştiriyoruz:

$\displaystyle \begin{pmatrix} -4 & 6 & -10 \\[1.1ex] -2 & -8 & 0 \\[1.1ex] 6 & -4 & 10 \end{pmatrix}+\begin{pmatrix} 5 & 0 & 0 \\[1.1ex] 0 & 5 & 0 \\[1.1ex] 0 & 0 & 5 \end{pmatrix} - \begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

İlk iki matrisi topluyoruz:

$\displaystyle \begin{pmatrix} 1 & 6 & -10 \\[1.1ex] -2 & -3 & 0 \\[1.1ex] 6 & -4 & 15 \end{pmatrix}-\begin{pmatrix} 18 & 0 & 6 \\[1.1ex] -9 & 12 & 3 \\[1.1ex] 9 & 6 & 21 \end{pmatrix}$

Son olarak matrislerin çıkarma işlemini gerçekleştiriyoruz:

$\displaystyle \begin{pmatrix} \bm{-17} & \bm{6} & \bm{-16} \\[1.1ex] \bm{7} & \bm{-15} & \bm{-3} \\[1.1ex] \bm{-3} & \bm{-10} & \bm{-6} \end{pmatrix}$

Matris skaler çarpımları ile ilgili bu alıştırmalar işinize yaradıysa, daha fazla tekrarlanan iki tür matris işlemi olan matrislerin toplanması ve matrislerin çarpımı konusunda adım adım çözülen alıştırmalarla pratik yapmaktan çekinmeyin.

Bir sayının matrise göre çarpımının özellikleri

Çok iyi bildiğiniz gibi birçok matris türü vardır: kare matrisler, üçgen matrisler, birim matris vb. Ancak neyse ki sayıların matrislere göre çarpımının tüm özellikleri tüm matris sınıfları için geçerlidir.

Skaler ve matrisler arasındaki çarpımın özellikleri şunlardır:

İlişkisel özellik:

$a \cdot (b \cdot A) = (a \cdot b) \cdot A$

Aşağıdaki iki işleme bakın çünkü 2 ile 3’ü nasıl çarparsak çarpalım aynı sonucu veriyorlar:

$\displaystyle 2 \cdot \left(3 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} \right) =2 \cdot \begin{pmatrix} 3 & 0 \\[1.1ex] 6 & -3 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

$\displaystyle (2 \cdot 3) \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} =6 \cdot \begin{pmatrix} 1 & 0 \\[1.1ex] 2 & -1 \end{pmatrix} = \begin{pmatrix} \bm{6} & \bm{0} \\[1.1ex] \bm{12} & \bm{-6} \end{pmatrix}$

Skalerlerin toplamına göre dağılım özelliği :

$(a+b) \cdot A = a \cdot A+ b \cdot A$

Aşağıdaki örnekte gördüğünüz gibi önce 1+2’yi toplayıp bir matrisle çarpsak, ya da matrisi ayrı ayrı 1 ve 2 ile çarpıp sonuçları toplasak da aynı şey oluyor:

$\displaystyle (1 + 2) \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} =3 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

$\displaystyle 1 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4 \end{pmatrix} + 2 \cdot \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5 \\[1.1ex] -2 & -4\end{pmatrix} = \begin{pmatrix} 2 & -1 \\[1.1ex] 3 & 5\\[1.1ex] -2 & -4 \end{pmatrix} + \begin{pmatrix} 4 & -2 \\[1.1ex] 6 & 10 \\[1.1ex] -4 & -8\end{pmatrix}= \begin{pmatrix} \bm{6} & \bm{-3} \\[1.1ex] \bm{9} & \bm{15} \\[1.1ex] \bm{-6} & \bm{-12} \end{pmatrix}$

Matris toplamına göre dağılım özelliği :

$a \cdot \left(A + B \right) = a \cdot A + a \cdot B$

Başka bir deyişle, iki matematiksel matrisin toplanıp ardından bir sayıyla çarpılması, iki matrisin aynı sayıyla ayrı ayrı çarpılıp sonuçların toplanmasına eşdeğerdir. Aşağıdaki örnekte şunları kontrol edebilirsiniz:

$\displaystyle 4 \cdot \left( \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+\begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} \right) =4 \cdot \begin{pmatrix} 2 & 1 \\[1.1ex] 6 & 3 \end{pmatrix}= \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

$\displaystyle 4 \cdot \begin{pmatrix} 3 & -2 \\[1.1ex] 6 & -1 \end{pmatrix}+ 4 \cdot \begin{pmatrix} -1 & 3 \\[1.1ex] 0 & 4 \end{pmatrix} = \begin{pmatrix} 12 & -8 \\[1.1ex] 24 & -4 \end{pmatrix}+\begin{pmatrix} -4 & 12 \\[1.1ex] 0 & 16 \end{pmatrix} = \begin{pmatrix} \bm{8} & \bm{4} \\[1.1ex] \bm{24} & \bm{12} \end{pmatrix}$

Nötr elemanın özelliği:

$1 \cdot A = A$

Bu nedenle, bir matrisi 1 ile çarparken matrisi değiştirmeyiz:

$\displaystyle 1 \cdot \begin{pmatrix} 5 & -4 & 0 \\[1.1ex] 1 & 3 & -3 \\[1.1ex] 2 & 9 & 4 \end{pmatrix}=\begin{pmatrix} \bm{5} & \bm{-4} & \bm{0} \\[1.1ex] \bm{1} & \bm{3} & \bm{-3} \\[1.1ex] \bm{2} & \bm{9} & \bm{4} \end{pmatrix}$

Bunların hepsi bir skaler ve bir matrisin çarpımının özellikleridir, dolayısıyla bu makalenin sonudur. Umarız hoşunuza gitmiştir ve her şeyden önce sayıların çarpımını matrislerle nasıl çözeceğinizi öğrenmişsinizdir.

Öte yandan çarpmayla bağlantılı ve çok faydalı olan diğer matris işlemleri de kuvvetlerdir. Merak ediyorsanız size matrisin kuvvetinin ne olduğunu ve nasıl çözüleceğini öğreneceğiniz sayfayı bırakıyoruz.

Bir sayı bir matrisle nasıl çarpılır?

Örnek:

Bir sayıyı bir matrisle çarpmayla ilgili çözülmüş problemler

1. Egzersiz:

Egzersiz 2:

Egzersiz 3:

Egzersiz 4:

Bir sayının matrise göre çarpımının özellikleri

Yorum bırakın Yanıtı iptal et