Bu sayfada polinomun ne olduğunu ve bir polinomun sayısal değerinin nasıl hesaplanacağını öğreneceksiniz. Ayrıca bir polinomun sayısal değerinin adım adım çözüldüğü örnekleri ve alıştırmaları görebileceksiniz.
Bir polinomun sayısal değeri nedir?
Matematikte bir P(x) polinomunun x=a değerine yani P(a) sayısal değeri, polinomun x değişkeninin a sayısı ile değiştirilmesi ve belirtilen hesaplamaların yapılmasıyla elde edilen sonuçtur. polinom ifadesinde.
Bir polinomun sayısal değeri kavramını daha iyi anlayabilmeniz için aşağıda bunun nasıl hesaplandığını bir örnekle gösteriyoruz:
Bir polinomun sayısal değeri nasıl hesaplanır
Artık bir polinomun sayısal değerinin matematiksel tanımını bildiğimize göre, bir örnek kullanarak bir polinomun sayısal değerinin nasıl belirleneceğini görelim:
- Aşağıdaki polinomun x=2 için sayısal değeri nedir?
![]()
Polinomun sayısal değerini bulmak için söz konusu polinomun problemin verdiği değerde değerlendirilmesi, yani değişkenin yerine başka bir değer konulması gerekir.
![]()
polinomun ifadenin değerine göre oranı. Bu nedenle bu durumda harfi değiştirmemiz gerekir.
![]()
2 için:
![]()
Ve değeri polinomun cebirsel ifadesine yerleştirdiğimizde işlemleri gerçekleştiririz. O halde ilk önce kuvvetleri çözelim:
![]()
Şimdi çarpımları hesaplıyoruz:
![]()
Son olarak terimleri ekleyip çıkarıyoruz:
![]()
Sonuç olarak x=2 polinomunun sayısal değeri 21’e eşittir.
Gördüğünüz gibi bir polinomun sayısal değerini bulmak çok karmaşık değildir ancak bazı çok yararlı uygulamaları vardır. Örneğin, bir polinomun sayısal değerinin nasıl bulunacağını bilmek, polinomlarla ilgili çok önemli bir teorem olan kalan teoremini kullanabilmek için çok önemlidir. Bu bağlantıya tıklayın ve kalan teoreminin ne olduğunu öğrenin, açıklamasını, kullanım örneklerini ve adım adım çözülmüş alıştırmaları bulacaksınız.
Polinomların Sayısal Değerlerine Örnekler
Bir polinomun sayısal değerinin nasıl elde edileceğini anlamanız için sizi diğer çözülmüş örneklerle baş başa bırakıyoruz:
örnek 1
- Polinomun sayısal değerini hesaplayın
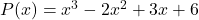
İçin

![Rendered by QuickLaTeX.com \begin{aligned} P(-1) & =(-1)^3-2\cdot (-1)^2+3\cdot (-1)+6 \\[2ex] & = -1-2\cdot 1+3\cdot (-1)+6 \\[2ex] & =-1-2-3+6 \\[2ex]&= \bm{0} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3293713c5e12fac56d94be90f6bfc6e5_l3.png)
Bu durumda polinomun sayısal değeri 0’a eşittir. Bunun polinomların özelliklerinden kaynaklanan sonuçları vardır, çünkü faktör teoremi sayesinde polinomlar arasındaki belirli bölümlerin geri kalanının ne olacağını bilebiliriz. Daha fazla bilgi edinmek için bu teoremin ne olduğunu ve ne işe yaradığını açıkladığımız önceki bağlantıya tıklayın.
Örnek 2
- Polinomun sayısal değerini belirleyin
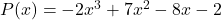
İçin
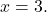
![Rendered by QuickLaTeX.com \begin{aligned} P(3) & =-2\cdot 3^3+7\cdot 3^2-8\cdot 3-2 \\[2ex] & =-2\cdot 27+7\cdot 9-8\cdot 3-2 \\[2ex] & =-54+63-24-2 \\[2ex]&= \bm{-17} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-ad8b1145d569157b4e771adfae674e2c_l3.png)
Şu ana kadar sadece klasik yöntemle bir polinomun sayısal değerinin nasıl belirleneceğini gördük ama bilmelisiniz ki başka bir yöntem daha var. Daha spesifik olarak, bir polinomun sayısal değerini Ruffini yöntemiyle de hesaplayabilirsiniz. Ayrıca bu prosedürü nasıl kullanacağınızı da bilmelisiniz, bu nedenle bağlantıdaki ayrıntılı açıklamaya göz atmanızı öneririz.
İki veya daha fazla değişkenli bir polinomun sayısal değeri
Sadece bir değişkeni olan bir polinomun sayısal değerini nasıl bulacağımızı gördük. Ama… birden fazla değişkeni olan bir polinomun sayısal değerini nasıl elde edersiniz?
Bir polinomun 2 veya daha fazla harfi varsa, sayısal değeri de aynı şekilde hesaplanmalıdır; yani önce polinomdaki her değişkeni karşılık gelen değeriyle değiştirin ve ardından polinom işlemlerini çözün .
Örnek olarak, aşağıda çözülmüş bu tür bir sorununuz var:
- Çok değişkenli polinomun sayısal değerini bulun
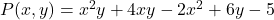
değerler için
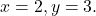
Öncelikle her değişkeni karşılık gelen değeriyle değiştiririz, yani harfi değiştiririz.
![]()
2 için ve harfi değiştiriyoruz
![]()
3’e kadar:
![]()
Güçleri çözüyoruz:
![]()
Şimdi ürünleri hesaplıyoruz:
![]()
Son olarak toplama ve çıkarma işlemlerini yapıyoruz:
![]()
Yani talimat verileri için polinomun sayısal değeri 41’e eşdeğerdir.
Bir polinomun sayısal değerine ilişkin çözülmüş alıştırmalar
1. Egzersiz
X=-2 için P(x) polinomunun sayısal değeri nedir?
![]()
Polinomun sayısal değerini bulmak için, ifadede verilen değeri polinom ifadesinde yerine koymamız ve elde edilen işlemleri çözmemiz yeterlidir:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-4\cdot (-2)^2+3\cdot (-2)+8 \\[2ex] & =-2\cdot (-8)-4\cdot 4+3\cdot (-2)+8 \\[2ex] & =+16-16-6+8 \\[2ex]&= \bm{2} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-93b7cf1a6c7e930a0a70fc8302f4012d_l3.png)
Alıştırma 2
Aşağıdaki kesirli polinomun sayısal değerini x=4 olarak hesaplayın.
![]()
Polinomun kesirleri olsun veya olmasın, polinomun sayısal değerini bulma prosedürü her zaman aynıdır. Bu nedenle x değişkenini 4 ile değiştirmeli ve hesaplamaları çözmeliyiz:
![Rendered by QuickLaTeX.com \begin{aligned} P(4) & =\cfrac{1}{2} \cdot 4^2-\cfrac{5}{4}\cdot 4+ 7 \\[2ex] & =\cfrac{1}{2} \cdot 16-\cfrac{5}{4}\cdot 4+ 7\\[2ex] & =8-5+7 \\[2ex]&= \bm{10} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-04fa4389b5e7c5257937ad35aed07c7b_l3.png)
Alıştırma 3
X=3, y=5 ve z=-2 değerleri için polinomun sayısal değerini belirleyin
![]()
Çok değişkenli polinomun sayısal değerini belirlemek için problemde verilen değerleri cebirsel ifadede yerine koymak ve ortaya çıkan işlemleri çözmek yeterlidir:
![Rendered by QuickLaTeX.com \begin{aligned} P(3,5,-2) & =3^2\cdot 5\cdot (-2)+4\cdot 5^2\cdot (-2)^2-3\cdot 3^2\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =9\cdot 5\cdot (-2)+4\cdot 25\cdot 4-3\cdot 9\cdot (-2)+6\cdot 3\cdot 5 \cdot (-2) \\[2ex] & =-90+400+54-180\\[2ex]&= \bm{184} \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-29683a91c14427a8ea42c3518e59e53f_l3.png)
Alıştırma 4
Polinom göz önüne alındığında
![]()
parametre değerini hesapla
![]()
böylece
![]()
Bu problemde bilinmeyenin değerini bulmak için
![]()
denklemi çözmemiz gerekiyor
![]()
![]()
Bu nedenle öncelikle P(-2) değerini hesaplamaya çalışıyoruz:
![Rendered by QuickLaTeX.com \begin{aligned} P(-2) & =-2\cdot (-2)^3-3\cdot (-2)^2+5\cdot (-2)+k \\[2ex] & =-2\cdot (-8)-3\cdot 4+5\cdot (-2)+k \\[2ex] & =+16-12-10+k\\[2ex]&=-6+k \end{aligned}](https://mathority.org/wp-content/ql-cache/quicklatex.com-3b58398099c8033b93a559e2f0c87f1a_l3.png)
Şimdi elde edilen ifadeyi 5’e eşitliyoruz:
![]()
![]()
Ve son olarak ortaya çıkan denklemi çözüyoruz:
![]()
![]()