Burada bunların ne olduklarına ve bir polinomun tüm parçalarına (derece, değişkenler, bağımsız terim vb.) nasıl adlandırıldıklarına dair açıklama bulacaksınız. Ek olarak, çeşitli örnekleri görebileceksiniz ve bir polinomun bazı kısımlarını çözülmüş alıştırmalarla uygulayabileceksiniz.
Ancak bir polinomun tüm parçalarının ne olduğunu görmeden önce, kavramı tam olarak anlamak için matematiksel tanımını hızlıca gözden geçirelim: Bir polinom , farklı derecelerdeki monomların toplanması veya çıkarılmasıyla oluşan cebirsel bir ifadedir.
Bir polinomun parçaları nelerdir?
Bir polinomun parçaları şunlardır:
- Terimler : polinomun her tek terimli kısmı.
- Katsayılar : Polinomun her bir terimine eşlik eden sayılar.
- Derece : Polinom değişkeninin yükseltildiği en büyük üs.
- Değişken : Polinomun sahip olduğu harftir.
- Ana Terim : Polinomun en yüksek dereceli terimidir.
- Bağımsız terim : Polinomun değişken içermeyen terimi.
- Baskın katsayı : polinomun baskın teriminin katsayısı.
Polinomun yalnızca bir değişkeni varsa derecesi, terimlerinin en büyük üssüne eşittir. Ancak polinomun iki veya daha fazla değişkeni varsa, bir işlem yapılması gerektiğinden derecesini bilmek daha zordur. İki (veya daha fazla) değişkenli bir polinomun derecesi için aşağıdaki bağlantıya tıklayarak bunun nasıl yapıldığını öğrenin.
Bir polinomun parçaları nasıl belirlenir
Bir polinomun parçaları veya elemanları görsel olarak kolayca bulunabilir. Bunun nasıl yapıldığını aşağıdaki şemada görün:
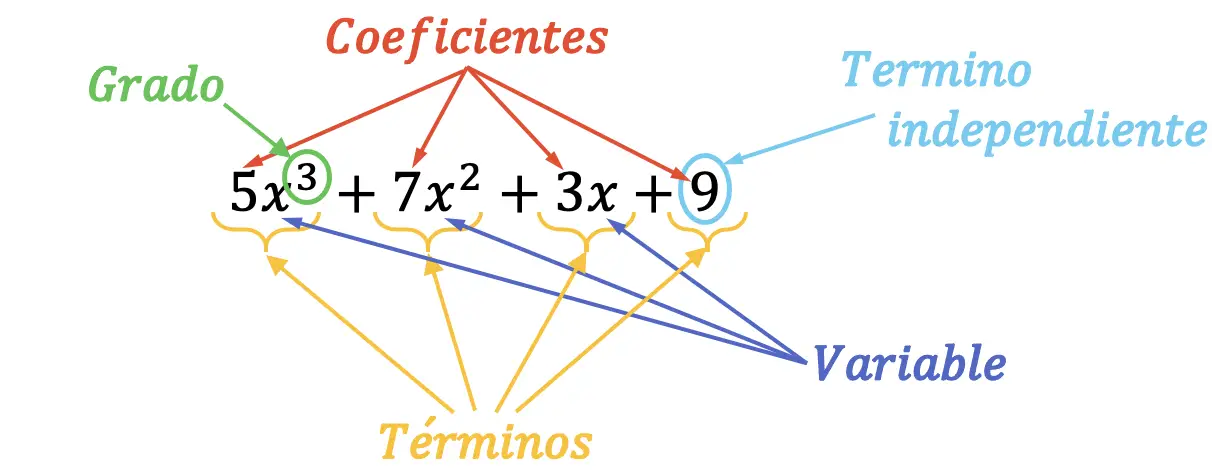
Üçüncü dereceden olan önceki polinomun tüm parçaları işaretlenmiştir. Ayrıca söz konusu polinomun ana terimi en yüksek dereceli monom olduğundan yaklaşık 5×3’tür . Benzer şekilde polinomun baş katsayısı da baş terimin katsayısı olduğundan 5’tir.
Bu durumda polinomun tek bir değişkeni vardır ve bu nedenle yalnızca tek bir derece türü vardır. Ancak polinom çok değişkenli olduğunda, bir değişkenin mutlak derecesi ile göreceli derecesi arasında ayrım yapmanız gerektiğini bilmelisiniz. Yukarıda bıraktığım linkte her birinin nelerden oluştuğunu görebilirsiniz ⬆⬆ ( iki değişkenli polinomun derecesi ).
Bir Polinomun Parçalarına Örnekler
Bir polinomun parçalarının anlamını ve gerçekleştirdikleri işlevi anlamayı tamamlamak için, herhangi bir polinom türünün parçalarını belirlemeye yönelik bazı örnekler göreceğiz:
örnek 1
Aşağıdaki ikinci dereceden (derece 2) polinomun parçalarını tanımlayın:
![]()
- Terimler: 4x 2 , -8x, 1
- Katsayılar: 4, -8, 1
- 2. yıl
- Değişken: x
- Ana terim: 4×2
- Bağımsız yetki: 1
- Direksiyon katsayısı: 4
Öte yandan, bu örnekteki polinomun trinomial olarak adlandırıldığını da belirtmek gerekir. Bu tür polinomun ne olduğunu üç terimli örneklerinde görebilirsiniz. Ayrıca, binom adı verilen başka bir polinom türü de ilginizi çekebilir (bununla bazı işlemleri yapmak daha kolaydır), binom örneklerinde onu özel kılan şeyin ne olduğunu görebilirsiniz.
Örnek 2
Aşağıdaki polinomun parçalarını bulun:
![]()
- Terimler: y 3 , 9y 2 , -5y, 3
- Katsayılar: 1, 9, -5, 3
- 3. yıl
- değişkenler: ve
- Ana terim: ve 3
- Bağımsız yetki: 3
- Direksiyon katsayısı: 1
Bu örnekte görebileceğiniz gibi, bir monomun önünde sayı yoksa bu onun katsayısının bir olduğu anlamına gelir. Yani bu polinomun baş katsayısı 1’e eşittir.
Bir polinomun bölümlerine ilişkin çözülmüş alıştırmalar
Bir polinomun tüm parçalarının adlarını hatırlamanıza yardımcı olmak amacıyla sizin için çeşitli çözümlü alıştırmalar hazırladık. Onlarla ilgili tüm sorularınızı bize yorumlarda sorabilirsiniz. ⬇⬇
1. Egzersiz
Aşağıdaki polinomun tüm parçalarını bulun:
![]()
Bu alıştırmadaki polinomun bağımsız bir terimi yoktur çünkü tüm terimler en az bir değişkenden (veya harften) oluşur.
Terimler: 2×4 , 6×2 , x
Katsayılar: 2, 6, 1
Seviye 4
Değişken: x
Ana terim: 2×4
Bağımsız terim: yok
Direksiyon katsayısı: 2
Alıştırma 2
Aşağıdaki polinomun tüm parçalarını bulun:
![]()
Bu problemdeki polinom iki değişkenden oluşur: x ve y. Henüz:
Terimler: -7x 4 y 2 , 3x 4 , -5y 2 , xy, -10
Katsayılar: -7, 3, -5, 1, -10
6. yıl
Değişkenler: x, y
Ana terim: -7x 4 ve 2
Bağımsız yetki: -10
Direksiyon katsayısı: -7
Gördüğünüz gibi, bunun gibi polinomları çözmek için birden fazla değişkenli bir polinomun derecesinin nasıl hesaplanacağını bilmeniz gerekir. Hala bunu nasıl yapacağınızdan emin değilseniz, yukarıdaki Polinomun Parçaları Nelerdir? bölümündeki bağlantıya göz atmanızı öneririm. ( iki değişkenli bir polinomun derecesi ). ⬆⬆ Adım adım açıklamanın yanı sıra çeşitli örnekleri de bulacaksınız.
Her ne kadar kökten farklı bir kavram olsa da, buraya kadar geldiyseniz bir sayının polinom ifadesinin ne olduğunu bilmek de mutlaka ilginizi çekecektir. Bu pek çok insanın bilmediği ama aslında çok faydalı bir şey.