Bir polinomun kökleri nasıl hesaplanır? (çözülmüş alıştırmalar)

Bu sayfada bir polinomun köklerinin ne olduğunu ve nasıl hesaplandığını öğreneceksiniz. Ayrıca bir polinomun kökleriyle ilgili adım adım çözülen örnekleri ve alıştırmaları görebileceksiniz.

Bir polinomun kökleri nelerdir?

Matematikte bir polinomun kökleri (veya sıfırları), polinomu iptal eden değerlerdir. Yani, bir polinomun kökleri, polinomda değerlendirildiğinde sayısal değeri 0’a eşit olan değerlerin tamamıdır.

Sonunda,

$x=a$

polinomun bir köküdür

$P(x)$

Evet

$P(a)=0.$

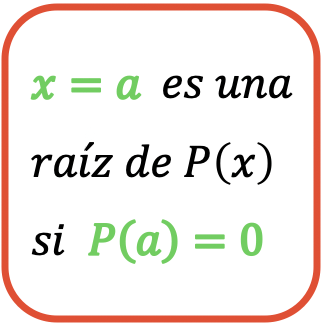
Örneğin, aşağıdaki polinomumuz varsa:

$P(x)=x^2-3x+2$

Polinomun x=1 noktasındaki sayısal değeri sıfıra eşit olduğundan, polinomun köklerinden birinin 1 olduğunu doğrulayabiliriz:

$P(1)=1^2-3\cdot 1+2 = 1-3+2 \color{blue} \bm{= 0}$

Öte yandan 3 polinomun kökü değildir çünkü polinomu iptal eden bir değer değildir veya başka bir deyişle polinomun x=3 noktasındaki sayısal değeri sıfırdan farklıdır:

$P(3)=3^2-3\cdot 3+2 = 9-9+2=2 \color{blue} \bm{\neq 0}$

Muhtemelen şimdi bir polinomun kökünün ne olduğunu daha iyi anlıyorsunuz, ama bir polinomun kaç kökü olduğunu bilmek istemez miydiniz? Veya bir polinomun tüm kökleri nasıl bulunur? Bir sonraki bölümde göreceğimiz şey tam olarak budur.

Bir polinomun tüm kökleri nasıl hesaplanır?

Bir polinomun tüm köklerini bulmak için aşağıdaki adımları izlemelisiniz:

Öncelikle polinomun bağımsız teriminin tüm bölenleri hesaplanır.
İkinci olarak, önceki adımda bulunan tüm değerler polinomda değerlendirilir.
Son olarak, polinomdaki bir sayı değerlendirilirken sayısal değeri sıfıra eşitse, söz konusu sayı polinomun bir köküdür. Aksi halde söz konusu sayı polinomun bir köküne karşılık gelmez.

Bu prosedür kalan teoreminden türetilmiştir, bu özel prosedürün nedenini öğrenmek için bu bağlantıya tıklayın.

Bir polinomun köklerini hesaplama örneği

Bir polinomun köklerinin nasıl alınacağını daha iyi anlayabilmeniz için aşağıda bir örneği adım adım çözeceğiz.

Aşağıdaki polinomun tüm kökleri nelerdir?

$P(x) = x^2-5x+6$

Öncelikle bağımsız terimin bölenlerini bulmalıyız çünkü bir polinomun her kökü aynı zamanda bağımsız terimin de böleni olur. Yani 6’nın bölenleri:

6’nın bölenleri: +1, -1, +2, -2, +3, -3

Bir sayı bölen ise negatifinin de bölen olduğunu unutmayın. Çünkü bir sayı pozitif ve negatif sayılara bölünebilir.

Dolayısıyla polinomun olası kökleri veya sıfırları şöyledir: ±1, ±2, ±3. Dolayısıyla tüm bu değerler için polinomun sayısal değerini belirlememiz gerekiyor. Ve bunu yapmak için, bu değerleri, x’in olduğu polinomun ifadesinde yerine koyarız:

$P(1) = 1^2 -5\cdot 1 +6= 1 -5 +6 =2$

$P(-1) = (-1)^2 -5\cdot (-1) +6 =1+5+6 = 12$

$P(2) = 2^2 -5\cdot 2 +6 =4-10+6= \color{blue} \bm{0}$

$P(-2) = (-2)^2 -5\cdot (-2) +6 =4+10+6 =20$

$P(3) = 3^2 -5\cdot 3 +6 =9-15+6=\color{blue} \bm{0}$

$P(-3) = (-3)^2 -5\cdot (-3) +6 =9+15+6 =30$

Yani polinom yalnızca x değişkeni +2 veya +3 olduğunda kaybolur, dolayısıyla polinomun kökleri şunlardır:

Polinomun kökleri veya sıfırları : +2 ve +3

Öte yandan, polinomun derecesi kadar kökü olduğuna dikkat edin, yani polinom ikinci dereceden olduğundan iki kökü vardır. Bir polinomun köklerinin özelliklerinde (aşağıda), bu özelliğin neden her polinom için geçerli olduğunu göreceğiz.

Az önce bir polinomun köklerini bulmanın bir yolunu gördük. Ancak bunu başarmanın başka yöntemleri de var; örneğin bir polinomun köklerini Ruffini kuralıyla da bulabilirsiniz. Ruffini kuralının örneklerini görmek için aşağıdaki bağlantıya tıklayın; burada bu iyi bilinen yöntemin nelerden oluştuğunu ve ayrıca iki prosedür arasındaki farkların neler olduğunu keşfedeceksiniz.

Bir polinomun köklerinin özellikleri

Bir polinomun kökleri veya sıfırları aşağıdaki özelliklere sahiptir:

Daha önce gördüğümüz gibi, bir polinomun tamsayı kökleri (veya sıfırları), polinomun bağımsız teriminin bölenleridir.

Bir polinomun tüm köklerini biliyorsak, söz konusu polinomu aşağıdaki türdeki binomların çarpımları şeklinde ifade edebiliriz.
$(x-a).$

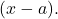
Örneğin polinom

$P(x) =x^3+3x^2-x-3$

3 kökü vardır

$x=+1, x=-1$

$x=-3.$

Bu nedenle polinomu, her biri değişken tarafından oluşturulan faktörlerin 3 çarpımı şeklinde yeniden yazabiliriz.

$x$

ve bir kökün işareti değişti:

$\displaystyle\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60} P(x) =x^3+3x^2-x-3 \ \longrightarrow \ \text{ra\'ices} \begin{cases} x=\color{verd}\bm{+1} \\[2ex] x=\color{vermell}\bm{-1} \\[2ex] x=\color{blau}\bm{-3}\end{cases}$

$\definecolor{vermell}{HTML}{F44336}\definecolor{blau}{HTML}{2196F3}\definecolor{verd}{HTML}{27AE60}P(x) =x^3+3x^2-x-3 = (x\color{verd}\bm{-1}\color{black})\cdot (x\color{vermell}\bm{+1}\color{black}) \cdot (x\color{blau}\bm{+3}\color{black})$

Buna polinom çarpanlara ayırma denir. Aslında bir polinomun köklerini belirlemenin ana uygulamalarından biri, bunların onu çarpanlara ayırmak için kullanılmasıdır. Aşağıdaki bağlantıdan bu çok özel işlemin nelerden oluştuğunu öğrenebilir ve ayrıca çözülmüş polinomları çarpanlara ayırma alıştırmaları ile pratik yapabilirsiniz.

Bir polinomun derecesinin gösterdiği kadar kökü vardır. Yani, ikinci dereceden bir polinomun 2 kökü olacak, üçüncü dereceden bir polinomun 3 kökü olacak, dördüncü dereceden bir polinomun 4 kökü olacak, vb.

Bir polinomun bağımsız bir terimi yoksa, köklerinden birinin 0 olduğu anlamına gelir. Bu durumda köklerin geri kalanı, en düşük derecedeki monomun katsayısının bölenleri olmalıdır.

Örneğin aşağıdaki polinomun bağımsız terimi yoktur:

$P(x) =x^3+x^2-2x$

Yani polinomun bir kökü mutlaka 0 olmalıdır. Geri kalan kökler ise en düşük dereceli terimin katsayısının, yani -2’nin bölenleridir. Daha doğrusu, diğer kökler

$x=+1$

$x=-2,$

polinomun tüm kökleri şöyledir:

Polinomun kökleri veya sıfırları: 0, +1 ve -2

Bir polinomun kökleri belirlenemediğinde ona indirgenemez polinom denir.

Örneğin aşağıdaki polinomun köklerini hesaplamaya çalışacağız:

$P(x) =x^2+3x-1$

Polinomun mümkün olan tek kökleri -1’in bölenleridir, yani -1 ve +1. Bu nedenle polinomu şu değerlere göre değerlendiriyoruz:

$P(1) = 1^2 +3\cdot 1 -1= 1 +3 -1 =3 \neq 0$

$P(-1) = (-1)^2 +3\cdot (-1)-1 =1-3-1 =-3 \neq 0$

Hiçbir durumda polinom iptal edilmez, dolayısıyla kökleri yoktur ve bu nedenle indirgenemez bir polinomdur.

Polinom birkaç polinomun çarpımından oluştuğunda, kökleri hesaplamak için bu çarpımı yapmak gerekli değildir, ancak polinomun kökleri her faktörün köklerinin çarpımıdır.

Örneğin, aşağıdaki polinomumuz varsa:

$P(x) = (x-2) \cdot (x+1)$

Polinomların köklerinin ikinci özelliğinden, sol polinomun kökünün +2, sağ polinomun kökünün -1 olduğu sonucunu çıkarabiliriz.

$\displaystyle (x-2) \ \longrightarrow \ \text{ra\'iz} \ x=+2$

$\displaystyle (x+1) \ \longrightarrow \ \text{ra\'iz} \ x=-1$

Dolayısıyla iki faktörün çarpımından elde edilen polinomun kökleri, bunların ilgili kökleridir, yani +2 ve -1.

$\displaystyle P(x) = (x-2) \cdot (x+1) \ \longrightarrow \ \text{ra\'ices} \ \begin{cases}x=+2 \\[2ex] x=-1 \end{cases}$

Polinomların köklerine ilişkin çözülmüş alıştırmalar

1. Egzersiz

olup olmadığını belirleyin

$x = -4$

aşağıdaki polinomun bir köküdür:

$P(x)=x^3+2x^2-11x-12$

Çözümü görün

olup olmadığını öğrenmek için

$x=-4$

polinomun bir kökü ise onu bu değere göre değerlendirmemiz gerekir. Henüz:

$\begin{aligned}P(-4)& =(-4)^3+2\cdot (-4)^2-11\cdot (-4) -12 \\[2ex] & = -64+2\cdot 16 +44 -12 \\[2ex] & = -64+32+44 -12 \\[2ex] & = 0 \end{aligned}$

Polinomun sayısal değeri

$x=-4$

sıfırdır, dolayısıyla polinomun etkili bir köküdür.

Alıştırma 2

Aşağıdaki polinomun tüm köklerini hesaplayın:

$P(x)=x^2-3x+2$

Çözümü görün

İlk olarak polinomun olası köklerini bulmak için bağımsız terimin bölenlerini bulmamız gerekir. Yani 2’nin bölenleri:

2’nin bölenleri: +1, -1, +2, -2

Dolayısıyla polinomun olası kökleri veya sıfırları ±1 ve ±2’dir. Dolayısıyla tüm bu değerlerde polinomun ne kadar olduğunu hesaplamamız gerekiyor:

$P(1)=1^2-3\cdot 1+2 =1-3+2=0$

$P(-1)=(-1)^2-3\cdot (-1)+2 =1+3+2=6$

$P(2)=2^2-3\cdot 2+2 =4-6+2=0$

$P(-2)=(-2)^2-3\cdot (-2)+2 =4+6+2=12$

Böylece, x +1 veya +2 olduğunda polinom kaybolur, dolayısıyla polinomun kökleri şunlardır:

Polinomun kökleri veya sıfırları : +1 ve +2

Alıştırma 3

Aşağıdaki polinomun köklerini bulun:

$P(x)=x^3-x^2-4x+4$

Çözümü görün

Bir polinomun kökü aynı zamanda bağımsız terimin de böleni olduğundan, önce bağımsız terimin bölenlerini bulmalıyız. Yani 4’ün bölenleri:

4’ün bölenleri: +1, -1, +2, -2, +4, -4

Dolayısıyla polinomun olası kökleri veya sıfırları ±1, ±2 ve ±4’tür. Bu nedenle polinomun sayısal değerini tüm bu değerlerde bulmalıyız:

$P(1)=1^3-1^2-4\cdot 1+4 =1-1-4+4=0$

$P(-1)=(-1)^3-(-1)^2-4\cdot (-1)+4 =-1-1+4+4=6$

$P(2)=2^3-2^2-4\cdot 2+4 =8-4-8+4=0$

$P(-2)=(-2)^3-(-2)^2-4\cdot (-2)+4 =-8-4+8+4=0$

$P(3)=3^3-3^2-4\cdot 3+4 =27-9-12+4=10$

$P(-3)=(-3)^3-(-3)^2-4\cdot (-3)+4 =-27-9+12+4=20$

Dolayısıyla polinom yalnızca x +1, +2 veya -2 olduğunda kaybolur; dolayısıyla polinomun kökleri şunlardır:

Polinomun kökleri veya sıfırları : +1, +2 ve -2

Alıştırma 4

Aşağıdaki polinomun köklerini bulun:

$P(x)=x^3-6x^2+8x$

Çözümü görün

Bu durumda polinomun bağımsız terimi yoktur. Dolayısıyla yukarıda açıklanan köklerin dördüncü özelliğine göre polinomun köklerinden birinin 0 olması gerektiğini biliyoruz.

Polinomun kökleri:

$x=0$

Ayrıca bu durumda olası kökler bağımsız terimin bölenleri değil, en düşük dereceli terimin katsayısının yani 8’in bölenleridir:

8’in bölenleri: +1, -1, +2, -2, +4, -4, +8, -8

Yani polinomun olası kökleri veya sıfırları ±1, ±2, ±4 ve ±8’dir. Bu nedenle polinomun sayısal değerini tüm bu değerlerde hesaplamamız gerekir:

$P(1)=1^3-6\cdot 1^2+8\cdot 1 = 1-6+8=3$

$P(-1)=(-1)^3-6\cdot (-1)^2+8\cdot (-1) = -1-6-8=-15$

$P(2)=2^3-6\cdot 2^2+8\cdot 2 = 8-24+16=0$

$P(-2)=(-2)^3-6\cdot (-2)^2+8\cdot (-2) = -8-24-16=-48$

$P(4)=4^3-6\cdot 4^2+8\cdot 4 = 64-96+32=0$

$P(-4)=(-4)^3-6\cdot (-4)^2+8\cdot (-4) = -64-96-32=-192$

$P(8)=8^3-6\cdot 8^2+8\cdot 8 = 512-384+64=192$

$P(-8)=(-8)^3-6\cdot (-8)^2+8\cdot (-8) = -512-384-64=-960$

Yani x +2 veya +4 olduğunda polinom kaybolur, yani bu değerler polinomun kökleridir. Ancak problemin başında bulduğumuz kök 0’ı da eklememiz gerekiyor. Sonuç olarak polinomun tüm kökleri şunlardır:

Polinomun kökleri veya sıfırları : 0, +2 ve +4

Alıştırma 5

Aşağıdaki polinomun köklerini hesaplamak için polinomların köklerinin özelliklerini kullanın:

$P(x)=(x-1)(x+3)(x^2-x-2)$

Çözümü görün

Köklerin altıncı özelliğinde gördüğümüz gibi polinom faktörlerin çarpımından oluştuğunda tüm polinomun kökleri her faktörün kökleri olduğundan tüm kökleri hesaplamaya gerek yoktur.

Ayrıca polinomların köklerinin ikinci özelliğinden birinci faktörün kökünün +1, ikinci faktörün kökünün -3 olduğu sonucunu çıkarabiliriz.

$\displaystyle (x-1) \ \longrightarrow \ \text{ra\'iz} \ x=+1$