Bir parametreye dayalı bir dizinin aralığı -

Bu sayfada bir tablonun parametreye göre sıralamasının nasıl hesaplanacağını göreceksiniz. Ayrıca, bir parametreye dayalı olarak bir matrisin aralığının nasıl bulunacağına ilişkin adım adım örnekler ve çözümlü alıştırmalar da bulacaksınız.

Matrislerin sırasını parametrelerle inceleme prosedürünü tam olarak anlamak için, bir matrisin sırasını determinantlara göre nasıl hesaplayacağınızı zaten bilmeniz önemlidir. Bu yüzden okumaya devam etmeden önce bu iki şeyi öğrenmenizi öneririz.

Bir parametreye dayalı olarak bir dizinin aralığı nasıl hesaplanır? Örnek:

Farklı parametre değerlerine dayalı olarak A matrisinin aralığını belirler
$\displaystyle a :$

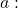
$\displaystyle A= \begin{pmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{pmatrix}$

A matrisi 3. mertebeden bir matris olduğu için en fazla 3. sırada olacaktır. Bu nedenle yapmamız gereken ilk şey, 3×3’lük matrisin tamamının determinantını Sarrus kuralıyla çözmek ve bunun rütbe 3 olup olamayacağını görmek:

$\displaystyle \begin{aligned} \begin{vmatrix} a+1 & -1 & a+1 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & a \end{vmatrix} & =-a(a+1)+0+0+a+1-0-0 \\ & =-a^2-a+a+1 \\[1.5ex] & =-a^2+1 \end{aligned}$

Determinantın sonucu parametrenin bir fonksiyonudur

$\displaystyle a$

. Bu nedenle, tablonun ne zaman 2. sırada, ne zaman 3. sırada olacağını görmek için sonucu 0’a eşitliyoruz :

$\displaystyle -a^2+1 = 0$

Ve ortaya çıkan denklemi çözüyoruz:

$\displaystyle a^2 = 1$

$\displaystyle \sqrt{a^2} = \sqrt{1}$

$\displaystyle \bm{a = \pm 1}$

Bu nedenle ne zaman

$\displaystyle a$

+1 de olsa, -1 de olsa 3×3 determinantı 0 olacak ve dolayısıyla matrisin rütbesi 3 olmayacaktır.

$\displaystyle a$

+1 ve -1’den farklıysa determinantı 0’dan farklı olacaktır ve bu nedenle matrisin derecesi 3 olacaktır.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Şimdi bakalım ne zaman olacak

$\displaystyle \bm{a=+1} :$

$\displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & -1 & 2 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & 1 \end{pmatrix}$

Daha önce gördüğümüz gibi, ne zaman

$\displaystyle a$

1 ise matrisin determinantı 0’dır. Bu nedenle rütbesi 3 olamaz. Şimdi matrisin içinde 0’dan farklı bir 2×2 determinantı , örneğin sol üst köşeyi hesaplamaya çalışıyoruz:

$\displaystyle \begin{vmatrix} 2 & -1 \\[1.1ex] 0 & -1 \end{vmatrix} =-2-0= -2 \neq 0$

2. derecenin determinantı 0’dan farklıdır. Dolayısıyla parametre ne zaman

$\displaystyle a$

veya +1 ise matrisin sırası 2 olacaktır:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Matrisin aralığını gördükten sonra

$\displaystyle a \neq +1,-1$

ve ne zaman

$\displaystyle a=+1$

bakalım ne zaman olacak

$\displaystyle \bm{a = -1} :$

$\displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 0 & -1 & 0 \\[1.1ex] 0 & -1 & 0 \\[1.1ex] 1 & -2 & -1 \end{pmatrix}$

Başlangıçta gördüğümüz gibi,

$\displaystyle a$

es -1 ve matrisin determinantı 0’dır. Bu nedenle rütbe 3’e ayarlanamaz. Bu nedenle matriste 0’dan farklı, örneğin daha düşük bir 2×2 determinantıyla karşılaşmaya çalışmalıyız. matrisin bir parçası. SOL:

$\displaystyle \begin{vmatrix} 0 & -1 \\[1.1ex] 1 & -2 \end{vmatrix} = 0-(-1)= 1\neq 0$

2. boyutun determinantı 0’dan farklıdır. Dolayısıyla parametre ne zaman

$\displaystyle a$

veya -1 ise tablonun sıralaması 2 olacaktır:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Bu nedenle A matrisinin sıralamasının parametrenin aldığı değere bağlı olduğu 3 farklı durum bulduk.

$\displaystyle a.$

İşte özeti :

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Artık parametreye bağlı matrislerin aralığını nasıl tartışacağınızı bildiğinize göre, aşağıdaki adım adım alıştırmaları yaparak pratik yapabilirsiniz. Bunları çözmek için belirleyicilerin özellikleri mutlaka işinize yarayacaktır, o yüzden eğer onlar hakkında çok net bilginiz yoksa öncelikle her birinin örneklerle açıklandığı bağlantılı sayfaya bir göz atmanızı tavsiye ederim.

Sabit parametre tabanlı matris aralığı sorunları

1. Egzersiz

Parametre değerine göre aşağıdaki tablonun aralığını inceleyin

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}$

Çözüme bakın

A matrisi 3×3 matris olduğundan en fazla 3. sıraya sahip olacaktır. Bu nedenle yapmamız gereken ilk şey, tüm matrisin determinantını (Sarrus kuralıyla) çözerek bunun 3. mertebede olup olamayacağını görmektir:

$\displaystyle \begin{vmatrix} 3 & 1 & a \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix} =0-8+2a-4a+12-0 =-2a+4$

Dizinin ne zaman Rank 2, ne zaman Rank 3 olacağını görmek için sonucu 0’a eşitliyoruz:

$\displaystyle -2a+4=0$

$\displaystyle -2a=-4$

$\displaystyle a=\cfrac{-4}{-2} = 2$

Bu nedenle ne zaman

$\displaystyle a$

2’den farklıysa, 3×3 determinantı 0’dan farklı olacaktır ve dolayısıyla matrisin rütbesi 3 olacaktır.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq 2 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Şimdi bakalım ne zaman olacak

$\displaystyle a=2 :$

$\displaystyle a = 2 \longrightarrow A= \begin{pmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 3 & 1 & 2 \\[1.1ex] 2 & 2 & -4 \\[1.1ex] 2 & 1 & 0 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 3 & 1 \\[1.1ex] 2 & 2 \end{vmatrix} = 6-2 = 4 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = 2 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Bu nedenle A matrisinin aralığının parametrenin aldığı değere göre değiştiği 2 durum bulduk:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 2 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 2\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Alıştırma 2

Parametre değerine göre aşağıdaki tablonun aralığını bulun

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{pmatrix}$

Çözüme bakın

$\displaystyle \begin{aligned} \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] a & 1 & 3 \\[1.1ex] -2 & -2 & a \end{vmatrix} & =2a-12-2a+2+12-2a^2 \\ &=2-2a^2\end{aligned}$

Dizinin ne zaman Rank 2, ne zaman Rank 3 olacağını görmek için sonucu 0’a eşitliyoruz:

$\displaystyle 2-2a^2=0$

$\displaystyle -2a^2=-2$

$\displaystyle a^2=\cfrac{-2}{-2}$

$\displaystyle a^2=1$

$\displaystyle a=\pm 1$

Bu nedenle ne zaman

$\displaystyle a$

+1 ve -1’den farklıysa 3×3 determinantı 0’dan farklı olacaktır ve dolayısıyla matrisin rütbesi 3 olacaktır.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq +1, -1 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Şimdi bakalım ne zaman olacak

$\displaystyle a=+1 :$

$\displaystyle a = +1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] 1 & 1 & 3 \\[1.1ex] -2 & -2 & 1 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 2 & 1 \\[1.1ex] 1 & 3 \end{vmatrix} = 6-1 = 5 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = +1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Şimdi bakalım ne zaman olacak

$\displaystyle a=-1 :$

$\displaystyle a = -1 \longrightarrow A= \begin{pmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 2 & 2 & 1 \\[1.1ex] -1 & 1 & 3 \\[1.1ex] -2 & -2 & -1 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 2 & 2 \\[1.1ex] -1 & 1 \end{vmatrix} =2-(-2) = 4 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -1 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Bu nedenle A matrisinin aralığının, parametrenin aldığı değere bağlı olarak değiştiği 3 durum bulduk:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq +1,-1 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = +1\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -1\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Alıştırma 3

Parametre değerine göre aşağıdaki tablonun aralığını hesaplar

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{pmatrix}$

Çözüme bakın

$\displaystyle \begin{aligned} \begin{vmatrix} a+1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & a-3 \end{vmatrix} & =(a+1)(a-3) +2+0-5+6(a+1)-0 \\ & = a^2-3a+a-3 +2-5+6a+6 \\[1.5ex] & =a^2+4a\end{aligned}$

Dizinin ne zaman Rank 2, ne zaman Rank 3 olacağını görmek için sonucu 0’a eşitliyoruz:

$\displaystyle a^2+4a=0$

Bu tamamlanmamış ikinci dereceden bir denklem olduğundan ortak bir çarpan çıkarıyoruz:

$\displaystyle a(a+4)=0$

Ve her terimi 0’a eşitliyoruz:

$\displaystyle a(a+4)=0 \longrightarrow \begin{cases} \bm{a = 0} \\[2ex] a+4=0 \ \longrightarrow \ \bm{a=-4}\end{cases}$

Çözüm olarak 0 ve -4’ü elde ettik. Bu nedenle ne zaman

$\displaystyle a$

0 ve -4’ten farklıysa 3×3 determinantı 0’dan farklı olacaktır ve dolayısıyla matrisin rütbesi 3 olacaktır.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq 0, -4 \ \longrightarrow \ Rg(A)=3} \phantom{33} \\[-2ex] & \end{array} }$

Şimdi bakalım ne zaman olacak

$\displaystyle a=0 :$

$\displaystyle a = 0 \longrightarrow A= \begin{pmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} 1 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -3 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} 1 & 1 \\[1.1ex] 0 & 1 \end{vmatrix} = 1-0 = 1 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = 0 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Şimdi bakalım ne zaman olacak

$\displaystyle a=-4 :$

$\displaystyle a = -4 \longrightarrow A= \begin{pmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{pmatrix}$

$\displaystyle \begin{vmatrix} A \end{vmatrix} = \begin{vmatrix} -3 & 1 & -5 \\[1.1ex] 0 & 1 & -2 \\[1.1ex] -1 & 3 & -7 \end{vmatrix}= 0$

$\displaystyle \begin{vmatrix} -3 & 1 \\[1.1ex] 0 & 1\end{vmatrix} =-3-0 = -3 \neq 0$

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -4 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Bu nedenle A matrisinin aralığının, parametrenin aldığı değere bağlı olarak değiştiği 3 durum bulduk:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq 0,-4 \longrightarrow \ Rg(A)=3} \phantom{33} \\[3ex] \color{black} \bm{a = 0\ \longrightarrow \ Rg(A)=2} \\[3ex] \color{black} \bm{a = -4\ \longrightarrow \ Rg(A)=2} \\ & \end{array} }$

Alıştırma 4

Parametrenin değerine göre aşağıdaki 3×4 boyut matrisinin kapsamını bulun

$\displaystyle a :$

$\displaystyle A=\begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&a \end{pmatrix}$

Çözüme bakın

Herhangi bir 4×4 determinantı hesaplayamadığımızdan A matrisi en fazla 3. sırada olacaktır. Bu nedenle yapmamız gereken ilk şey, 3. dereceden tüm olası determinantları (Sarrus kuralıyla) çözmek ve bunun 3. dereceden olup olmadığını görmektir:

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-3&-2\\[1.1ex] 4&12&8\\[1.1ex] 2&6&4 \end{vmatrix} & =-48-48-48+48+48+48 =\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-3&1\\[1.1ex] 4&12&-4\\[1.1ex] 2&6&a \end{vmatrix} & =-12a+24+24-24-24+12a=\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -1&-2&1\\[1.1ex] 4&8&-4\\[1.1ex] 2&4&a \end{vmatrix} & =-8a+16+16-16-16+8a=\bm{0}\end{aligned}$

$\displaystyle \begin{aligned} \begin{vmatrix} -3&-2&1\\[1.1ex] 12&8&-4\\[1.1ex] 6&4&a \end{vmatrix} & =-24a+48+48-48-48+24a=\bm{0}\end{aligned}$

Değeri ne olursa olsun, 3. dereceden tüm olası determinantların sonuçları 0’dır.

$\displaystyle a$

. Bu nedenle matris hiçbir zaman 3. sırada olmayacaktır çünkü hangi değeri aldığı önemli değildir.

$\displaystyle a$

0’dan başka 3×3’lük bir determinantın asla olamayacağını.

Şimdi 2 × 2 boyutunun determinantlarını deneyeceğiz. Bununla birlikte, aşağıdakiler dışında 2. dereceden tüm determinantlar da 0 verir:

$\displaystyle \begin{aligned} \begin{vmatrix} 8&-4\\[1.1ex] 4&a \end{vmatrix} & =8a+16 \end{aligned}$

Şimdi sonucu 0’a eşitliyoruz ve denklemi çözüyoruz:

$\displaystyle 8a+16=0$

$\displaystyle 8a=-16$

$\displaystyle a=\cfrac{-16}{8} =-2$

Bu nedenle ne zaman

$\displaystyle a$

-2’den farklıysa 2×2 determinantı 0’dan farklı olacaktır ve dolayısıyla matrisin rütbesi 2 olacaktır.

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black}\phantom{33} \bm{a \neq -2 \ \longrightarrow \ Rg(A)=2} \phantom{33} \\[-2ex] & \end{array} }$

Şimdi bakalım ne zaman olacak

$\displaystyle a=-2 :$

$\displaystyle a = -2 \longrightarrow A= \begin{pmatrix} -1&-3&-2&1\\[1.1ex] 4&12&8&-4\\[1.1ex] 2&6&4&-2 \end{pmatrix}$

Daha önce gördüğümüz gibi, ne zaman

$\displaystyle a$

-2 ise, 2. dereceden tüm determinantlar 0’dır. Bu nedenle, 2. dereceden olamaz. Ve 0’dan farklı en az bir 1×1 determinant mevcut olduğundan, bu durumda matrisin rütbesi 1’dir:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\[-2ex] \color{black} \phantom{33} \bm{a = -2 \ \longrightarrow \ Rg(A)=1} \phantom{33} \\[-2ex] & \end{array} }$

Bu nedenle A matrisinin aralığının parametrenin aldığı değere göre değiştiği 2 durum bulduk:

$\displaystyle \color{blue} \boxed{ \begin{array}{c} \\ \color{black} \phantom{33} \bm{a \neq -2 \longrightarrow \ Rg(A)=2} \phantom{33} \\[3ex] \color{black} \bm{a = -2\ \longrightarrow \ Rg(A)=1} \\ & \end{array} }$

Bir parametreye dayalı olarak bir dizinin aralığı nasıl hesaplanır? Örnek:

Sabit parametre tabanlı matris aralığı sorunları

1. Egzersiz

Alıştırma 2

Alıştırma 3

Alıştırma 4

Yorum bırakın Yanıtı iptal et