Bir nokta ile bir çizgi arasındaki mesafe

Burada bir nokta ile çizgi arasındaki mesafeyi hesaplamak için kullanılan formülü bulacaksınız. Ek olarak, noktalar ve doğrular arasındaki mesafelerle ilgili çeşitli örnekleri ve çözülmüş alıştırmaları ve hatta bu işlemin sahip olduğu uygulamaları (örneğin, paralel çizgiler arasındaki mesafeyi bulma) görebileceksiniz.

Bir nokta ile çizgi arasındaki mesafenin formülü

Bir nokta ile bir çizgi arasındaki mesafe, o nokta ile bir çizgi arasındaki en kısa mesafedir. Matematiksel olarak bu minimum mesafe, noktadan doğruya çizilen ve doğruya dik olan doğru parçasının uzunluğuna eşittir.

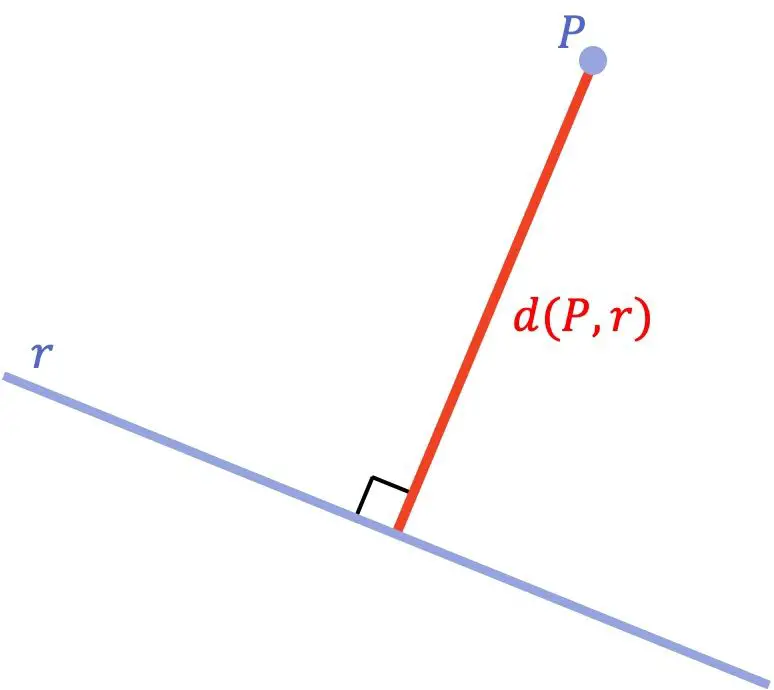
bir nokta ile bir çizgi arasındaki mesafe nedir

Bir nokta ile bir çizgi arasındaki mesafenin geometrik kavramını gördükten sonra, söz konusu mesafeyi hesaplamak için kullanılan formülün ne olduğuna bakalım:

Bir doğrunun örtülü (veya genel) denklemi ve bir düzlemdeki herhangi bir noktanın koordinatları göz önüne alındığında:

$r: \ Ax+By+C=0 \qquad \qquad P(p_x,p_y)$

Bir nokta ile bir çizgi arasındaki mesafenin formülü :

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Önemli: Formüldeki doğrunun denkleminin örtülü (veya genel) denklem biçiminde olduğuna dikkat edin; bu nedenle, eğer doğruyu başka bir denklem türünde ifade edersek, onu önce örtülü denklemine aktarmamız ve sonra formülü uygulayabiliriz.

Bir nokta ile çizgi arasındaki mesafeyi hesaplama örneği

Aşağıda bir nokta ile çizgi arasındaki mesafeyi hesaplamanın bir örneğini görebilirsiniz:

Nokta arasındaki mesafeyi bulun
$P$

ve kanun

$r:$

$P(2,-1) \qquad \qquad r: \ 3x+4y-5=0$

Nokta ile çizgi arasındaki mesafeyi hesaplamak için formülü uygulamanız yeterlidir:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Şimdi her terimi değeriyle değiştiriyoruz:

$d(P,r)= \cfrac{\lvert 3\cdot 2 + 4\cdot (-1)-5\rvert}{\sqrt{3^2+4^2}}$

Ve son olarak mesafeyi hesaplıyoruz:

$d(P,r)= \cfrac{\lvert 6 -4-5\rvert}{\sqrt{9+16}} =\cfrac{\lvert -3 \rvert}{\sqrt{25}} = \mathbf{\cfrac{3}{5}}$

İki paralel çizgi arasındaki mesafe

Bir doğru ile bir nokta arasındaki mesafeyi hesaplamanın uygulamalarından biri de paralel çizgiler arasındaki mesafeyi bulmaktır.

Açıkçası aşağıda açıklayacağımız kavramı anlamak için paralel çizgilerin ne olduğunu bilmeniz gerekir, dolayısıyla tanımlarını tam olarak bilmiyorsanız, size detaylı olarak açıkladığımız ve örnekleri de görebileceğiniz bir bağlantı bırakıyoruz. paralel çizgilerden.

İki paralel çizgi arasındaki mesafeyi bulmak için iki çizgiden birinin üzerinde bir nokta alın ve o noktadan diğer çizgiye olan mesafeyi hesaplamanız yeterlidir.

bir nokta ile bir çizgi arasındaki mesafe

Yani iki paralel çizgi arasındaki mesafeyi belirlemek için bir çizgi ile bir nokta arasındaki mesafe formülü de kullanılır.

Öte yandan formülü kullanırken 0 birimlik bir mesafe elde edersek bu, çizgilerin bir noktada birbirine değdiği ve dolayısıyla çizgilerin paralel olmadığı, kesiştiği, çakıştığı veya dik olduğu anlamına gelir. İsterseniz bu tip hatlar arasındaki farkları sitemizden inceleyebilirsiniz.

Şimdi bir örnek üzerinden iki paralel doğru arasındaki uzaklık problemini nasıl çözeceğimizi görelim:

Aşağıdaki iki paralel çizgi arasındaki mesafeyi bulun:

$r: \ 2x-4y-6=0 \qquad \qquad s: \ -x+2y+4=0$

Yapmamız gereken ilk şey çizgilerden birinde (istediğiniz çizgide) bir nokta almak. Bu durumda doğru üzerinde bir nokta hesaplayacağız.

$s.$

Bunu yapmak için değişkenlerden birine bir değer vermelisiniz, örneğin şunu yapacağız:

$x=0:$

$-x+2y+4 =0 \ \xrightarrow{x \ = \ 0} \ -0+2y+4=0$

Ve şimdi diğer değişkeni temizliyoruz (

$y$

) Bu noktada değerinin ne kadar olduğunu bilmek için elde edilen denklemin:

$2y=-4$

$y= \cfrac{-4}{2}$

$y= -2$

Bu nedenle doğrudan elde edilen nokta

$s$

Doğu:

$P(0,-2)$

Ve bir doğru üzerinde zaten bir noktamız olduğunda, o noktadan diğer doğruya olan mesafeyi aşağıdaki formülü kullanarak hesaplarız:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 2\cdot 0 + (-4)\cdot (-2) +(-6)\rvert}{\sqrt{2^2+(-4)^2}}= \cfrac{2}{\sqrt{20}}=\bm{0,45}$

Bir nokta ile çizgi arasındaki mesafe problemlerini çözdük

1. Egzersiz

Nokta arasındaki mesafeyi hesaplayın

$P$

ve kanun

$r:$

$P(4,2) \qquad \qquad r: \ 5x-3y+6=0$

Çözüme bakın

Bir nokta ile çizgi arasındaki mesafeyi bulmak için formülü uygulamanız yeterlidir:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Her terimi değeriyle değiştiririz ve mesafeyi hesaplarız:

$d(P,r)= \cfrac{\lvert 5\cdot 4 + (-3)\cdot 2+6\rvert}{\sqrt{5^2+(-3)^2}}=\cfrac{20}{\sqrt{34}}= \bm{3,43}$

Alıştırma 2

nokta arasındaki mesafe ne kadardır?

$P$

ve kanun

$r$

$P(-3,-1) \qquad \qquad r: \ y=-3x+5$

Çözüme bakın

Bu durumda doğrunun denklemi örtülü (veya genel) biçimdedir. Bunun yerine, bir noktadan bir çizgiye olan mesafe formülünü kullanmak için çizginin örtülü bir denklem olarak ifade edilmesi gerekir. Bu nedenle önce doğruyu dönüştürmeli ve bunu örtülü bir denkleme geçirmeliyiz (sadece denklemin aynı tarafındaki tüm terimleri aktarın):

$r: \ 3x+y-5=0$

Çizgi zaten açık bir biçimde olduğunda, artık bir nokta ile bir çizgi arasındaki uzaklık formülünü kullanabiliriz:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Bu nedenle her terimi kendi değeriyle değiştiririz ve mesafeyi hesaplarız:

$d(P,r)= \cfrac{\lvert 3\cdot (-3) + 1\cdot (-1)-5\rvert}{\sqrt{3^2+1^2}}=\cfrac{\lvert -9-1-5\rvert}{\sqrt{9+1}}=\cfrac{15}{\sqrt{10}}= \bm{4,74}$

Alıştırma 3

Aşağıdaki iki çizgi arasındaki mesafe ne kadardır?

$r: \ x+3y-4=0 \qquad \qquad s: \ 2x+6y+6=0$

Çözüme bakın

Öncelikle bunların iki paralel çizgi olduğunu doğrulayacağız. Bunun için değişkenlerin katsayıları

$x$

$y$

birbirleriyle orantılı olmalı ancak bağımsız terimlerle orantılı olmamalıdır:

$\cfrac{1}{2} = \cfrac{3}{6}\neq \cfrac{-4}{6} \ \longrightarrow \ \text{Paralelas}$

Aslında çizgiler paraleldir, dolayısıyla prosedürü uygulayabiliriz.

Şimdi doğrulardan birinden (istediğiniz noktadan) bir nokta almamız gerekiyor. Bu durumda doğru üzerinde bir nokta hesaplayacağız.

$s.$

Bunu yapmak için değişkenlerden birine bir değer atamalısınız, örneğin şunu yapacağız:

$x=0:$

$2x+6y+6=0 \ \xrightarrow{x \ = \ 0} \ 2\cdot 0+6y+6=0$

Ve şimdi diğer değişkeni temizliyoruz (

$y$

) bu noktadaki değerini bilmek için elde edilen denklemin:

$6y=-6$

$y= \cfrac{-6}{6}$

$y= -1$

Böylece çizgiden elde edilen nokta

$s$

Doğu:

$P(0,-1)$

Bir doğru üzerindeki bir noktayı bildiğimizde, o noktadan diğer doğruya olan mesafeyi aşağıdaki formülle hesaplarız:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

$d(P,r)= \cfrac{\lvert 1\cdot 0 + 3\cdot (-1) +(-4)\rvert}{\sqrt{1^2+3^2}}= \cfrac{7}{\sqrt{10}}=\bm{2,21}$

Alıştırma 4

Bilinmeyenlerin değerini hesaplayın

$k$

böylece nokta arasındaki mesafe

$P$

ve kanun

$r$

yani 5 birim.

$P(-2,5) \qquad \qquad r: \ 12x-5y+k=0$

çözümü gör

İlk önce bir nokta ile bir çizgi arasındaki mesafe formülünü uygulamalıyız:

$d(P,r)= \cfrac{\lvert A\cdot p_x + B\cdot p_y +C\rvert}{\sqrt{A^2+B^2}}$

Şimdi her terimi değeriyle değiştirip ifadeyi basitleştiriyoruz:

$d(P,r)= \cfrac{\lvert 12\cdot (-2) + (-5)\cdot 5+k\rvert}{\sqrt{12^2+(-5)^2}}= \cfrac{\lvert -24-25+k\rvert}{\sqrt{169}}=\cfrac{\lvert -49+k\rvert}{13}$

Problem cümlesi bize nokta ile doğru arasındaki mesafenin 5’e eşit olması gerektiğini söylüyor, dolayısıyla önceki ifadeyi 5’e eşitliyoruz:

$\cfrac{\lvert -49+k\rvert}{13}=5$

Ve ortaya çıkan denklemi çözüyoruz. Kesrin payının mutlak bir değeri vardır, bu nedenle mutlak değerin pozitif ve negatif olduğunu ayrı ayrı analiz etmeliyiz:

$\cfrac{+(-49+k)}{13}=5$