Bu makalede, bir fonksiyonun türevlenebilirliğini, yani bir fonksiyonun türevlenebilir olup olmadığını nasıl inceleyeceğinizi öğreneceksiniz. Ayrıca bir fonksiyonun türevlenebilirliği ile sürekliliği arasındaki ilişkiyi de göreceğiz. Son olarak parçalı bir fonksiyonun türevlenebilirliğini inceleyeceğiz.
Bir fonksiyonun türevlenebilirliği ve sürekliliği
Bir fonksiyonun bir noktadaki sürekliliği ve türevlenebilirliği aşağıdaki şekilde ilişkilidir:
- Bir fonksiyon bir noktada türevlenebilirse o noktada süreklidir.
- Bir fonksiyon bir noktada sürekli değilse o noktada türevlenebilir de değildir.
Ancak bu teoremin tersi yanlıştır: Bir fonksiyonun bir noktada sürekli olması onun o noktada her zaman türevlenebilir olduğu anlamına gelmez.
Ayrıca bir fonksiyonun bir noktada türevlenebilir olup olmadığını grafiksel gösteriminden de görebilirsiniz:
- Eğer düzgün bir nokta ise fonksiyon bu noktada türevlenebilirdir.
- Açısal bir nokta ise fonksiyon süreklidir ancak bu noktada türevlenebilir değildir.

x=0’da yumuşatma noktası :
Bu aşamada sürekli ve türevlenebilir fonksiyon.

x=2’deki açısal nokta :
fonksiyon süreklidir ancak bu aşamada türevlenebilir değildir.
Parçalı bir fonksiyonun türevlenebilirliği
Bir fonksiyonun sürekliliği ile türevlenebilirliği arasındaki ilişkiyi öğrendikten sonra, parçalı tanımlanmış bir fonksiyonun türevlenebilirliğini nasıl inceleyeceğimizi göreceğiz.
Parçalı bir fonksiyonun bir noktada türevlenebilir olup olmadığını o noktadaki yanal türevleri hesaplayarak anlayabilirsiniz:
- Bir noktadaki yanal türevler eşit değilse fonksiyon o noktada türevlenebilir değildir:
![]()
İndirilemez
![]()
- Bir noktadaki yanal türevler çakışıyorsa fonksiyon o noktada türevlenebilirdir:
![]()
Evet, farklılaştırılabilir
![]()
Not: Bir fonksiyonun bir noktada türevlenebilmesi için fonksiyonun o noktada sürekli olması gerekir. Bu nedenle yanal türevleri hesaplamadan önce fonksiyonun o noktada sürekli olduğundan emin olmamız gerekir. Bir noktada sürekliliğin nasıl çalışıldığını bilmiyorsanız aşağıdaki bağlantıdan nasıl yapıldığını görebilirsiniz:
➤ Bakınız: bir fonksiyonun bir noktadaki sürekliliği
Şimdi bir noktada parçalı tanımlanan bir fonksiyonun türevinin nasıl hesaplanacağına dair bir örnek görelim:
- x=2 noktasında parçalı olarak tanımlanan aşağıdaki fonksiyonun sürekliliğini ve türevlenebilirliğini inceleyin:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} 3x^2-6x & \text{si} & x<2 \\[2ex] 6\ln (x-1) & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-a98eee72521c68fd394eb6209a7d0a59_l3.png)
İki parçanın fonksiyonları kendi aralıklarında süreklidir ancak fonksiyonun x=2 kritik noktasında sürekli olup olmadığına bakmak gerekir. Bunu yapmak için fonksiyonun yanal limitlerini şu noktada çözüyoruz:
![]()
![]()
Kritik noktadaki yanal limitler bize aynı sonucu verdi, dolayısıyla fonksiyon x=2 noktasında süreklidir.
Fonksiyonun x=2’de sürekli olduğunu bildiğimizde, fonksiyonun o noktadaki türevlenebilirliğini inceleyeceğiz. Bunu yapmak için parça olarak tanımlanan fonksiyonun yanal türevlerini hesaplıyoruz :
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 6x-6 & \text{si} & x<2 \\[2ex] \cfrac{6}{x-1} & \text{si} & x\geq 2 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3709995609d0f69f382ff651e397c00a_l3.png)
Şimdi her bir yanal türevi kritik noktada değerlendireceğiz:
![]()
![]()
İki yanal türev bize aynı sonucu verdi, dolayısıyla fonksiyon x=2’de türevlenebilir ve türevin değeri 6’dır:
![]()
Öte yandan yanal türevler bize farklı bir sonuç vermiş olsaydı bu, fonksiyonun x=2’de türevlenemeyeceği anlamına gelirdi. Başka bir deyişle türev bu noktada mevcut olmayacaktır.
Son olarak, mutlak değer fonksiyonları parçalı olarak da tanımlanabildiğinden, bu prosedürün mutlak değer fonksiyonunun türevlenebilirliğini incelemek için de geçerli olduğunu unutmayın. Mutlak değer fonksiyonunun parçalara nasıl dönüştürüleceğini burada görebilirsiniz:
➤ Bakınız: mutlak değeri olan bir fonksiyonun parçalı olarak nasıl tanımlanacağı
Bir fonksiyonun türevlenebilirliğine ilişkin çözülmüş alıştırmalar
1. Egzersiz
Aşağıdaki parçalı fonksiyonun sürekliliğini ve türevlenebilirliğini inceleyin:
![Rendered by QuickLaTeX.com \displaystyle f(x)= \left\{ \begin{array}{lcl} x^3-4x^2 + 5 & \text{si} & x<1 \\[2ex] -x^2+3x & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-3656065bb8de98bd07da153f26fd326e_l3.png)
İki parçanın fonksiyonları süreklidir ancak fonksiyonun x=1 kritik noktasında sürekli olup olmadığına bakmalıyız. Bunu yapmak için fonksiyonun yanal limitlerini şu noktada çözüyoruz:
![]()
![]()
Kritik noktadaki iki yanal limit aynı sonucu verir, dolayısıyla fonksiyon x=1’de süreklidir.
Fonksiyonun kritik noktada sürekli olduğunu bildiğimizde, aynı noktada türevlenebilir olup olmadığını inceleyeceğiz. Bu nedenle yanal türevleri hesaplıyoruz:
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 3x^2-8x & \text{si} & x<1 \\[2ex] -2x+3 & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-42451fa799527167fe9a2e2259248870_l3.png)
Ve x=1’deki iki yanal türevi hesaplıyoruz;
![]()
![]()
Yanal türevler x=1 noktasında çakışmadığından fonksiyon bu noktada türevlenebilir değildir.
![]()
Alıştırma 2
Bölümlerde tanımlanan aşağıdaki fonksiyonun türevlenebilirliğini ve sürekliliğini analiz edin:
![\displaystyle f(x)= \left\{ \begin{array}{lcl} \sqrt{4x} & \text{si} & x\leq 1 \\[2ex] 2+\ln x & \text{si} & x> 1 \end{array} \right.” title=”Rendered by QuickLaTeX.com” height=”65″ width=”226″ style=”vertical-align: 0px;”></p>
</p>
<div class=](https://mathority.org/wp-content/ql-cache/quicklatex.com-0d118e3904c810abd15e427e9c7d0504_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} \cfrac{4}{2\sqrt{4x}} & \text{si} & x<1 \\[4ex] \cfrac{1}{x} & \text{si} & x\geq 1 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-8261f3d268b47d9171710997c8cc70bd_l3.png)
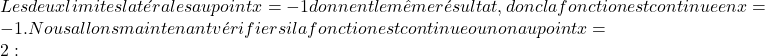
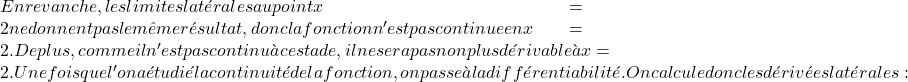
^2 & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-ce34d5d8a949fb3a0b904e9bf7d32f5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle f'(x)= \left\{ \begin{array}{lcl} 2e^{x-3} & \text{si} & x< 3 \\[2ex]2(x-b) & \text{si} & x\geq 3 \end{array} \right.](https://mathority.org/wp-content/ql-cache/quicklatex.com-d542fc9488644f0c144059ae1403d961_l3.png)