Bir fonksiyonun dönüm noktaları -

Burada bir fonksiyonun dönüm noktasının ne olduğunu ve bir fonksiyonun tüm dönüm noktalarının nasıl bulunacağını açıklıyoruz. Ayrıca bir fonksiyonun eğriliği ve bükülme noktalarıyla ilgili adım adım alıştırmalar bulacaksınız.

Bir fonksiyonun dönüm noktaları nelerdir?

Bir fonksiyonun bükülme noktaları, fonksiyonun grafiğinin eğriliğin değiştiği noktalardır, yani bir bükülme noktasında bir fonksiyonun içbükeyden dışbükeye veya tam tersi değiştiği noktalardır.

Bir fonksiyonun dönüm noktasına sahip olup olmadığı nasıl anlaşılır?

Dönüm noktasının tanımı göz önüne alındığında, belirli bir noktanın fonksiyonun dönüm noktası olup olmadığını nasıl anlayacağımızı görelim.

Bir fonksiyonun ikinci türevini iptal eden ve üçüncü türevinin sıfır olmayan noktalarda bir dönüm noktası vardır.

$\left.\begin{array}{l}f''(a)=0\\[2ex]f'''(a)\neq 0\end{array}\right\} \quad \bm{\longrightarrow} \quad x=a \text{ es un punto de inflexi\'on}$

Örnek olarak aşağıdaki üçüncü derece fonksiyonun dönüm noktalarını hesaplayacağız:

$f(x)=x^3-5x$

İlk olarak fonksiyonun ikinci ve üçüncü türevlerini hesaplıyoruz:

$f'(x)=3x^2-5$

$f''(x)=6x$

$f'''(x)=6$

Şimdi ikinci türevi 0’a eşitliyoruz ve elde edilen denklemi çözüyoruz:

$6x=0$

$x=0$

O zaman, eğer üçüncü türev bu noktada sıfır değilse, x=0 noktası fonksiyonun bir dönüm noktası olacaktır. Bizim durumumuzda üçüncü türev her zaman 6’ya eşittir.

$f'''(0)=6\neq 0$

Bu nedenle x=0 fonksiyonun bir dönüm noktasıdır.

Eğrilik nasıl incelenir ve bir fonksiyonun bükülme noktaları nasıl bulunur?

Az önce dönüm noktalarını bulmanın bir yöntemini gördük. Ancak normalde bir fonksiyonun eğriliğini incelemeye, yani bir fonksiyonun içbükeyliğini ve dışbükeyliğini belirlemeye ve oradan bükülme noktalarını hesaplamaya eğilimliyiz.

Bir fonksiyonun bükülme noktalarını eğriliğinden bulmak için aşağıdaki adımlar gerçekleştirilmelidir:

Fonksiyonun tanım kümesine ait olmayan noktaları bulun.
Fonksiyonun birinci türevini ve ikinci türevini hesaplayın.
İkinci türevin köklerini bulun, yani ikinci türevi iptal eden noktaları çözerek hesaplayın
$f''(x)=0$

.
Türevin kökleri ve fonksiyonun tanım kümesine ait olmayan noktalar ile aralıklar oluşturun.
Her aralığın bir noktasında ikinci türevin değerini hesaplayın.
İkinci türevin işareti, bu aralıktaki fonksiyonun içbükeyliğini veya dışbükeyliğini belirler:
- Fonksiyonun ikinci türevi pozitifse fonksiyon bu aralıkta dışbükeydir .
- Fonksiyonun ikinci türevi negatif ise fonksiyon bu aralıkta içbükeydir .
Bükülme noktaları, fonksiyonun dışbükeyden içbükeyliğe veya tersi yönde değiştiği noktalardır.

Bu prosedür kullanılarak bir fonksiyonun dönüm noktalarının nasıl hesaplandığını görebilmeniz için aşağıda bir örneği adım adım çözeceğiz:

Aşağıdaki polinom fonksiyonunun eğriliğini inceleyin ve dönüm noktalarını bulun:

$f(x)=x^4-6x^2$

Yapılacak ilk şey fonksiyonun tanım tanım kümesini hesaplamaktır. Bu bir polinom fonksiyonudur, dolayısıyla fonksiyonun tanım kümesi gerçek sayılardan oluşur, yani sürekli bir fonksiyondur:

$\text{Dom } f= \mathbb{R}$

Fonksiyonun tanım kümesini hesapladıktan sonra hangi noktalarda yerine getirildiğini incelememiz gerekiyor.

$f''(x)=0$

Bu nedenle ilk önce fonksiyonun birinci türevini hesaplıyoruz:

$f(x)=x^4-6x^2 \ \longrightarrow \ f'(x)= 4x^3-12x$

Daha sonra fonksiyonun ikinci türevini hesaplıyoruz:

$f'(x)=4x^3-12x \ \longrightarrow \ f''(x)= 12x^2-12$

Şimdi ikinci türevi 0’a eşitliyoruz ve denklemi çözüyoruz:

$f''(x)=0$

$12x^2-12=0$

$12x^2=12$

$x^2=\cfrac{12}{12}$

$x^2=1$

$\sqrt{x^2}=\sqrt{1}$

$x=\pm1$

Fonksiyonun tanım kümesini hesapladıktan sonra

$f''(x)=0$

sayı doğrusunda bulunan tüm kritik noktaları temsil ediyoruz:

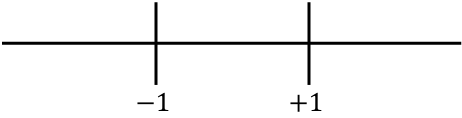
Şimdi fonksiyonun içbükey mi yoksa dışbükey mi olduğunu bilmek için her aralıkta ikinci türevin işaretini değerlendireceğiz. Bu nedenle her aralıkta bir nokta alıyoruz (asla kritik noktaları değil) ve bu noktada ikinci türevin hangi işarete sahip olduğuna bakıyoruz:

$f''(x)=12x^2-12$

$f''(-2) = 12\cdot (-2)^2-12 =36 \ \rightarrow \ \bm{+}$

$f''(0) = 12\cdot 0^2-12 = -12 \ \rightarrow \ \bm{-}$

$f''(2) = 12\cdot 2^2-12=36 \ \rightarrow \ \bm{+}$

İkinci türevin pozitif olması fonksiyonun dışbükey olduğu anlamına gelir.

$(\bm{\cup})$

ve ikinci türev negatifse bu, fonksiyonun içbükey olduğu anlamına gelir

$(\bm{\cap})$

. Bu nedenle fonksiyonun içbükeylik ve dışbükeylik aralıkları şöyledir:

Dışbükey

$(\bm{\cup})$

$\bm{(-\infty,-1) \cup (1,+\infty)}$

İçbükey

$(\bm{\cap})$

$\bm{(-1,1)}$

Ayrıca, x=-1 noktasında fonksiyon dışbükeyden içbükey hale gelir, dolayısıyla x=-1 fonksiyonun bir dönüm noktasıdır . Ve x=1’de fonksiyon içbükeyden dışbükeye gider, dolayısıyla x=1 aynı zamanda fonksiyonun bir dönüm noktasıdır .

Son olarak, dönüm noktalarının Y koordinatını bulmak için bulunan noktaları orijinal fonksiyonda yerine koyarız:

$f(-1)=(-1)^4-6(-1)^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (-1,-5)$

$f(1)=1^4-6\cdot 1^2 = 1-6 \cdot 1 = -5 \ \longrightarrow \ (1,-5)$

Dolayısıyla fonksiyonun dönüm noktaları şunlardır:

Dönüş noktası:

$\bm{(-1,-5)}$

$\bm{(1,-5)}$

Aşağıda incelenen fonksiyonun grafik gösterimini görebilirsiniz:

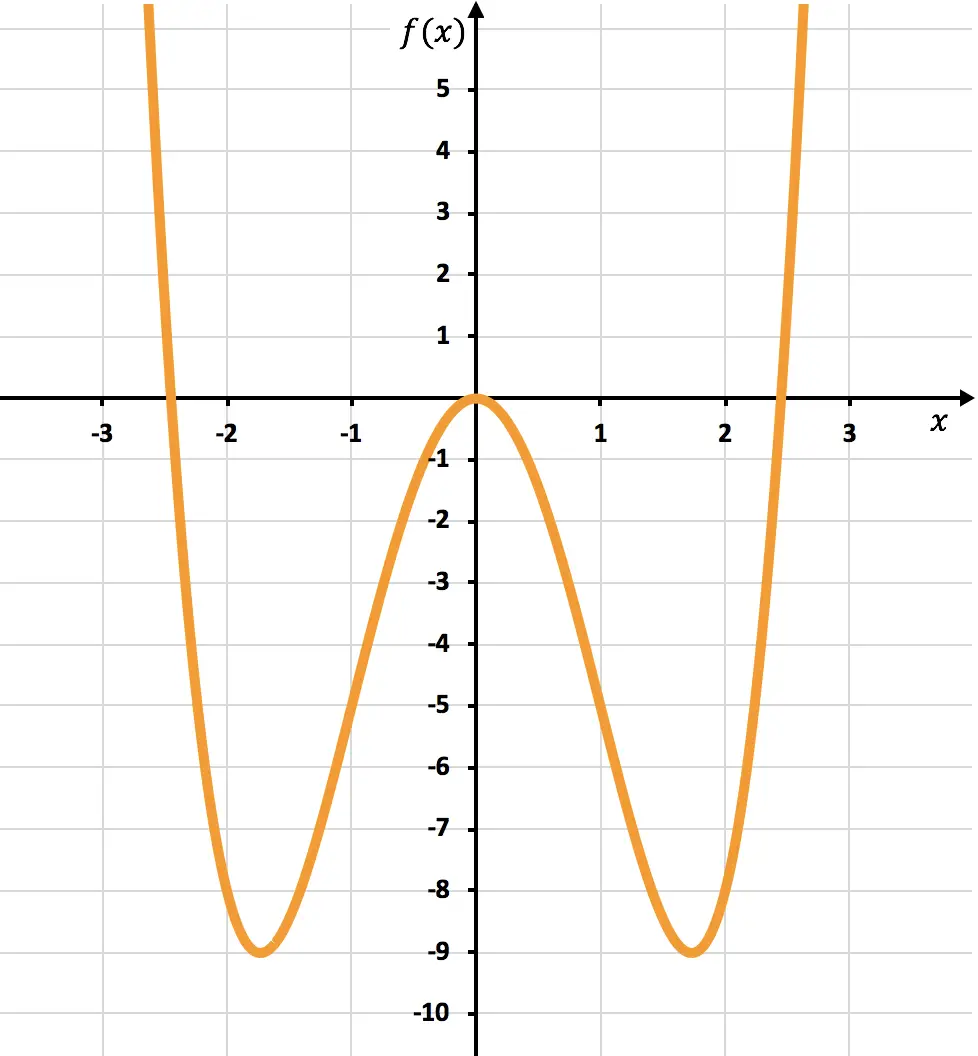
Grafikten görebileceğiniz gibi fonksiyon dışbükeyden gidiyor

$(\cup)$

içbükey olmak

$(\cap)$

Hakkında

$(-1,-5)$

eğriliği değiştiğinden beri. Öte yandan fonksiyon içbükeyden gidiyor

$(\cap)$

dışbükey olmak

$(\cup)$

Hakkında

$(1,-5)$

Çözülmüş dönme egzersizleri

1. Egzersiz

Aşağıdaki üstel fonksiyonun içbükeylik ve dışbükeylik aralıklarının yanı sıra bükülme noktalarını hesaplayın:

$f(x) = xe^x$

Çözümü görün

Yapılacak ilk şey fonksiyonun tanım tanım kümesini hesaplamaktır. Fonksiyon, alanı yalnızca gerçek sayılardan oluşan bir polinom fonksiyonundan (x) ve alanı aynı zamanda gerçek sayılardan oluşan bir üstel fonksiyondan ( ^ex ) oluşur. Bu nedenle fonksiyonun tanım kümesi gerçek sayılardan oluşur:

$\text{Dom } f= \mathbb{R}$

Şimdi fonksiyonun türevini hesaplayalım. Bu durumda fonksiyon iki fonksiyonun çarpımından oluşur, dolayısıyla fonksiyonu türetmek için bir çarpımın türevi formülünü uygulamamız gerekir:

$f'(x)=1 \cdot e^x+ x \cdot e^x$

$f'(x)=e^x +xe^x$

Daha sonra fonksiyonun ikinci türevini hesaplıyoruz:

$f''(x)= e^x + 1 \cdot e^x+ x \cdot e^x$

$f''(x)=e^x +e^x + xe^x = 2e^x +xe^x$

İkinci türevi 0’a eşitliyoruz ve denklemi çözüyoruz:

$f''(x)= 0$

$2e^x+xe^x= 0$

Ortak çarpanı çıkarıyoruz:

$e^x(2+x)=0$

Çarpmanın 0’a eşit olması için çarpımın iki unsurundan birinin sıfır olması gerekir. Bu nedenle her faktörü 0’a eşitliyoruz:

$\displaystyle e^x\cdot(2+x) =0 \longrightarrow \begin{cases} e^x=0 \ \color{red}\bm{\times}\color{black} \\[2ex] 2+x=0 \ \longrightarrow \ x= - 2 \end{cases}$

Başka bir sayıya yükseltilen bir sayı asla 0 ile sonuçlanamaz. Bu nedenle denklem

$e^x=0$

Çözümü yok.

Sağda elde edilen tüm tekil noktaları temsil ediyoruz:

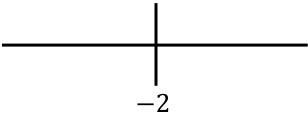
Şimdi fonksiyonun içbükey mi yoksa dışbükey mi olduğunu bilmek için her aralıktaki ikinci türevin işaretini değerlendireceğiz. Bunu yapmak için her aralıkta bir nokta alıyoruz ve o noktada hangi işaretin ikinci türevine sahip olduğuna bakıyoruz:

$f''(-3)= 2e^{-3} +(-3)\cdot e^{-3} = 0,1 - 0,15 = -0,05\ \rightarrow \ \bm{-}$

$f''(0)= 2e^0 +0\cdot e^0 = 2 \cdot 1 + 0 \cdot 1 =2+0= 2 \ \rightarrow \ \bm{+}$

İkinci türevin pozitif olması fonksiyonun dışbükey olduğu anlamına gelir.

$(\bm{\cup})$

ve ikinci türev negatifse bu, fonksiyonun içbükey olduğu anlamına gelir

$(\bm{\cap})$

. Bu nedenle içbükeylik ve dışbükeylik aralıkları şöyledir:

Dışbükey

$(\bm{\cup})$

$\bm{(-2,+\infty)}$

İçbükey

$(\bm{\cap})$

$\bm{(-\infty,-2)}$

Ek olarak, fonksiyon x=-2’de içbükeyden dışbükeye değişir, dolayısıyla x=-2, fonksiyonun bir dönüm noktasıdır .

Son olarak, noktanın Y koordinatını bulmak için bulunan dönüm noktasını orijinal fonksiyonda yerine koyarız:

$f(-2) = (-2)\cdot e^{-2} =-2e^{-2} \ \longrightarrow \ (-2,-2e^{-2})$

Sonuç olarak fonksiyonun tek dönüm noktaları şunlardır:

Dönüş noktası:

$\bm{(-2,-2e^{-2})}$

Alıştırma 2

İçbükeylik ve dışbükeylik aralıklarını inceleyin ve aşağıdaki rasyonel fonksiyonun bükülme noktalarını bulun:

$\displaystyle f(x)=\frac{x^3}{x^2-4}$

Çözümü görün

Öncelikle fonksiyonun tanım kümesini hesaplamamız gerekiyor. Bu rasyonel bir fonksiyon olduğundan, hangi sayıların fonksiyonun tanım kümesine ait olmadığını görmek için paydayı sıfıra eşitliyoruz:

$x^2-4= 0$

$x^2=4$

$\sqrt{x^2}=\sqrt{4}$

$x=\pm 2$

Bu, x -2 veya +2 olduğunda paydanın 0 olacağı anlamına gelir. Dolayısıyla fonksiyon mevcut olmayacaktır. Dolayısıyla fonksiyonun tanım kümesi x=-2 ve x=+2 dışındaki tüm sayılardan oluşur.

$\text{Dom } f= \mathbb{R}-\{-2, +2 \}$

İkinci olarak fonksiyonun birinci türevini hesaplıyoruz:

$f(x)=\cfrac{x^3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{3x^2 \cdot (x^2-4) - x^3 \cdot 2x }{\left(x^2-4\right)^2}$

$f'(x)= \cfrac{3x^4-12x^2-2x^4}{\left(x^2-4\right)^2} = \cfrac{x^4-12x^2}{\left(x^2-4\right)^2}$

Daha sonra ikinci türevi çözüyoruz:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 2\left(x^2-4\right)\cdot 2x }{ \left(\left(x^2-4\right)^2 \right)^2}$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^2 - \left(x^4-12x^2\right)\cdot 4x\left(x^2-4\right) }{\left(x^2-4\right)^4 }$

Tüm terimler çarpılır

$(x^2-4)$

. Bu nedenle kesri basitleştirebiliriz:

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right)^{\cancel{2}} - \left(x^4-12x^2\right)\cdot 4x\cancel{\left(x^2-4\right)} }{\left(x^2-4\right)^{\cancelto{3}{4}} }$

$f''(x)= \cfrac{\left(4x^3-24x\right)\cdot \left(x^2-4\right) - \left(x^4-12x^2\right)\cdot 4x}{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - \left(4x^5-48x^3\right) }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{4x^5-16x^3-24x^3+96x - 4x^5+48x^3 }{\left(x^2-4\right)^3 }$

$f''(x)= \cfrac{8x^3+96x }{\left(x^2-4\right)^3 }$

Şimdi fonksiyonun ikinci türevinin köklerini hesaplayalım:

$f''(x)= 0$

$\cfrac{8x^3+96x }{\left(x^2-4\right)^3 }=0$

Dönem

$\left(x^2-4\right)^3$

Bu, sol tarafın tamamını bölmeyi içerir, böylece bunu sağ tarafın tamamıyla çarpabiliriz:

$8x^3+96x =0\cdot \left(x^2-4\right)^3$

$8x^3+96x =0$

Ortak çarpanı çıkarıyoruz:

$x(8x^2+96)=0$

Çarpmanın 0’a eşit olması için çarpımın iki unsurundan birinin sıfır olması gerekir. Bu nedenle her faktörü 0’a eşitliyoruz:

$\displaystyle x\cdot(8x^2+96) =0 \longrightarrow \begin{cases} \bm{x =0} \\[2ex] 8x^2+96=0 \ \longrightarrow \ x^2=\cfrac{-96}{8}} = -12 \ \longrightarrow \ x= \sqrt{-12} \ \color{red}\bm{\times} \end{cases}$

$x= \sqrt{-12}$

Reel sayının negatif kökü olmadığı için çözüm de yoktur.

Şimdi elde edilen tüm kritik noktaları, yani tanım kümesine ait olmayan noktaları (x=-2 ve x=+2) ve ikinci türevi (x=0) iptal eden noktaları doğru üzerinde temsil ediyoruz:

Ve fonksiyonun içbükey mi yoksa dışbükey mi olduğunu bilmek için her aralıkta ikinci türevin işaretini değerlendiririz. Yani her aralıkta bir nokta alıyoruz ve o noktada hangi işaretin ikinci türevine sahip olduğuna bakıyoruz:

$f''(-3)=\cfrac{8(-3)^3+96(-3) }{\left((-3)^2-4\right)^3 } = \cfrac{-504}{125}=-4,03 \ \rightarrow \ \bm{-}$

$f''(-1)=\cfrac{8(-1)^3+96(-1) }{\left((-1)^2-4\right)^3 } = \cfrac{-104}{-27}=3,85 \ \rightarrow \ \bm{+}$

$f''(1)=\cfrac{8\cdot1^3+96\cdot 1 }{\left(1^2-4\right)^3 } = \cfrac{104}{-27}=-3,85 \ \rightarrow \ \bm{-}$

$f''(3)=\cfrac{8\cdot 3^3+96\cdot 3 }{\left(3^2-4\right)^3 } = \cfrac{504}{125}=4,03 \ \rightarrow \ \bm{+}$

İkinci türevin pozitif olması fonksiyonun dışbükey olduğu anlamına gelir.

$(\bm{\cup})$

ve ikinci türev negatifse bu, fonksiyonun içbükey olduğu anlamına gelir

$(\bm{\cap})$

. Bu nedenle içbükeylik ve dışbükeylik aralıkları şöyledir:

Dışbükey

$(\bm{\cup})$

$\bm{(-2,0)\cup (2,+\infty)}$

İçbükey

$(\bm{\cap})$

$\bm{(-\infty,-2)\cup (0,2)}$

Fonksiyon eğriliği üç noktada değiştirir, bu nedenle rasyonel fonksiyonun prensipte üç bükülme noktası olacaktır, bunlar x=-2, x=0 ve x=2. Ancak x=-2 ve x=+2 noktalarında eğrilikte değişiklik olmasına rağmen bunlar fonksiyonun tanım kümesine ait olmadıkları için dönüm noktaları değildir. Öte yandan x=0 noktasında eğrilikte bir değişiklik olur ve bu fonksiyona aittir, dolayısıyla fonksiyonun tek dönüm noktası x=0’dır.

Geriye kalan tek şey bükülme noktasının Y koordinatını hesaplamaktır:

$\displaystyle f(0)=\frac{0^3}{0^2-4} =\frac{0}{-4}=0\ \longrightarrow \ (0,0)$

Kısacası rasyonel fonksiyonun tek dönüm noktası koordinatların başlangıç noktasıdır:

Dönüş noktası:

$\bm{(0,0)}$

Alıştırma 3

Fonksiyonun olduğunu biliyoruz

$f(x)=x^3+ax^2+bx+c$

noktadan geçmek

$(3,1)$

göreceli olarak aşırı uç bir noktaya sahiptir

$x=1$

ve bir dönüm noktası

$x = 2$

. Bu bilgilerden parametre değerlerini hesaplayın

$a, b$

$c$

Çözümü görün

Fonksiyonun bir dönüm noktası olsun

$x= 2$

anlamına gelir

$f''(2)=0$

. Bu nedenle fonksiyonun ikinci türevini hesaplıyoruz

$x= 2$

ve bunu 0’a eşitledik:

$f(x) = x^3+ax^2+bx+c \ \longrightarrow \ f'(x)=3x^2+2ax+b$

$f'(x)=3x^2+2ax+b \ \longrightarrow \ f''(x)= 6x+2a$

$\left. \begin{array}{l} f''(2)=6\cdot 2+2a\\[2ex] f''(2)=0\end{array} \right\} \longrightarrow 6\cdot 2+2a=0$

Ve a parametresinin değerini bulmak için elde edilen denklemi çözüyoruz:

$6\cdot 2+2a=0$

$12+2a=0$

$2a=-12$

$a=\cfrac{-12}{2}$

$\bm{a=-6}$

Bu nedenle fonksiyon şöyle olacaktır:

$f(x)=x^3+ax^2+bx+c \ \xrightarrow{a \ = \ -6}\ f(x)=x^3-6x^2+bx+c$

Ayrıca, fonksiyonun aşırı bir durumu vardır.

$x= 1$

, Bu şu anlama geliyor

$f'(1)=0$

. Bu nedenle fonksiyonun birinci türevini hesaplıyoruz

$x= 1$

ve bunu 0’a eşitledik:

$f(x)=x^3-6x^2+bx+c \ \longrightarrow \ f'(x)=3x^2-12x+b$

$\left. \begin{array}{l} f'(1)=3\cdot 1^2-12\cdot 1+b\\[2ex] f'(1)=0\end{array} \right\} \longrightarrow 3\cdot 1^2-12\cdot 1+b=0$

Ve bilinmeyen b’nin değerini bulmak için elde edilen denklemi çözüyoruz:

$3\cdot 1^2-12\cdot 1+b=0$

$3 \cdot 1 -12 + b = 0$

$3 -12 + b = 0$

$b=+12-3$

$\bm{b=9}$

Bu nedenle fonksiyon şöyle olacaktır:

$f(x)=x^3-6x^2+bx+c \ \xrightarrow{b \ = \ 9} \ f(x)=x^3-6x^2+9x+c$

Öte yandan fonksiyonun (3,1) noktasından geçtiğini söylüyorlar. Yani,

$f(3)=1$

. Dolayısıyla c parametresinin değerini bulmak için bu koşulu uygulayabiliriz:

$\left. \begin{array}{l} f(3)=3^3-6\cdot 3^2+9\cdot3+c \\[2ex] f(3)=1 \end{array} \right\} \longrightarrow 3^3-6\cdot 3^2+9\cdot 3+c = 1$

Ve değerini bulmak için elde edilen denklemi çözüyoruz.

$b:$

$3^3-6\cdot 3^2+9\cdot 3+c = 1$

$27-6\cdot 9+27+c = 1$

$27-54+27+c = 1$

$c=1-27+54-27$

$\bm{c=1}$

Bu nedenle fonksiyon şöyle olacaktır:

$f(x)=x^3-6x^2+9x+c \ \xrightarrow{c \ = \ 1} \ f(x)=x^3-6x^2+9x+1$