Bir farkın karesi (veya çıkarma)

Burada bir farkın karesinin (veya çıkarmanın) dikkate değer özdeşlik formülünün ne olduğunu açıklıyoruz, yani size (ab) ² ifadesinin nasıl çözüldüğünü gösteriyoruz. Ayrıca örnekleri görebileceksiniz ve farkın karesinde çözülen alıştırmalarla pratik yapabileceksiniz. Ve son olarak bu dikkat çekici ürün tipinin formül gösterimini ve geometrik yorumunu gösteriyoruz.

Bir farkın (veya çıkarmanın) karesi nedir?

Bir farkın karesi veya bir çıkarmanın karesi dikkate değer özdeşliklerden (veya dikkate değer çarpımlardan) biridir, yani iki terimli bir binomun dörtlüsünün hesaplanmasını kolaylaştıran bir matematik kuralından oluşur: biri pozitif ve diğeri olumsuz.

Bu nedenle bir farkın karesinin cebirsel ifadesi (ab) ^2’dir .

Bir farkın karesi (veya çıkarma) formülü

Bu tür dikkat çekici özdeşliğin tanımını gördükten sonra, farkın karesini formülüyle nasıl çözeceğimizi göreceğiz:

bir farkın veya çıkarmanın karesi formülü

Yani bir farkın karesi, birinci terimin karesinden eksi birinci terimin ikinci çarpımının iki katı artı ikinci terimin karesine eşittir.

Yani, bir farkı veya kareli çıkarmayı hesaplamak için, her terimi yalnızca ikiye çıkarmakla kalmamalı, aynı zamanda bunları birlikte ve 2 ile çarpmanız gerekir.

Bunu hatırlamak önemlidir, çünkü kareleri çıkarırken çok yaygın bir hata, ürünü iki terimin arasına koymamak ve yalnızca azalmanın karesini ve çıkarma işleminin çıkarılmasını çözmektir:

A ile b arasındaki çarpımı unutmayın!

Fark (veya çıkarma) karelerine örnekler

Artık farkın karesinin formülünü bildiğimize göre onunla hesaplamalar yapabiliriz. Bunun nasıl yapıldığını görebilmeniz için, bir farkın karesinin (veya çıkarma işleminin) birkaç çözülmüş örneğini hazırladık.

örnek 1

Aşağıdaki farkın karesini çözün:

$(x-3)^2$

Bu bir kare çıkarma işlemidir, dolayısıyla formülünü uygulamanız gerekir:

$(a-b)^2=a^2-2ab+b^2$

Öyleyse bilinmeyenlerin değerlerinin ne olduğunu belirlememiz gerekiyor.

$a$

$b$

formülü. Bu durumda,

$a$

değişken

$x$

$b$

3 numaraya karşılık gelir:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (x-3)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=x \\[2ex] b=3 \end{array}$

Negatif işaretin bir parçası olmadığını unutmayın.

$b,$

ancak formülü doğru bir şekilde uygulamak için her zaman işareti olmayan sayıyı almalısınız.

Bu nedenle değerlerini zaten biliyoruz.

$a$

$b$

Bu nedenle, yalnızca bu değerleri formülde yerine koymamız gerekir:

kareli çıkarmanın binom alıştırmaları çözüldü

Örnek 2

Aşağıdaki kare çıkarma işleminin binomunu hesaplayın:

$(5x-2)^2$

Farkın karesi formülü şu şekildedir:

$(a-b)^2=a^2-2ab+b^2$

O halde öncelikle değerlerini belirlememiz gerekiyor.

$a$

$b$

formülü. Bu problemde,

$a$

monomial’i temsil eder

$5x$

$b$

binomun bağımsız terimine eşdeğerdir, yani 2:

$\left. \begin{array}{l} (a-b)^2\\[2ex] (5x-2)^2 \end{array} \color{red} \right\} \quad \color{red}\bm{\longrightarrow}\quad \color{black} \begin{array}{c} a=5x \\[2ex] b=2 \end{array}$

Son olarak parametrelerin değerini bildiğimizde

$a$

$b$

, kare çıkarma için basitçe binom formülünü uygularız:

$\begin{aligned} (5x-2)^2 & = (5x)^2-2\cdot 5x \cdot 2 + 2^2 \\[2ex] & = 25x^2-20x+4 \end{aligned}$

Farkın karesi formülünün kanıtı

Daha sonra çıkarma işleminin karesi formülünün nereden geldiğini çıkaracağız. Kanıtı ezberlemenize gerek olmasa da, arkasındaki matematiği anlamak yine de güzel.

Tüm çıkarma işlemlerinin binomunun ifadesinden başlarsak:

$(a-b)^2$

Açıkçası, önceki güç faktörün çarpımına eşittir

$(a-b)$

kendisi ile çarpılır:

$(a-b)^2= (a-b)\cdot (a-b)$

Şimdi dağılma özelliğini uygulayarak iki parantezi çarpıyoruz:

$\begin{aligned}(a-b)\cdot (a-b) & = a\cdot a +a\cdot (-b) - b\cdot a - b \cdot (-b) \\[2ex] & = a^2-ab-ba+b^2 \end{aligned}$

Formülü kanıtlamayı bitirmek için benzer terimleri bir arada gruplamamız gerekiyor:

$a^2-ab-ba+b^2 = a^2-2ab +b^2$

Çıkarmanın karesi formülünün matematiksel olarak kanıtlanması için:

$(a-b)^2=a^2-2ab+b^2$

İlginç bir şekilde, bir kare çıkarmanın binom ifadesinin açılımı aynı zamanda tam kare üç terimli olarak da bilinir.

Bir farkın karesinin geometrik yorumu

Bir farkın karesi kavramını anlamayı tamamlamak için bu dikkate değer eşitliğin geometrik olarak nasıl yorumlanacağını göreceğiz.

Kenar uzunlukları olan aşağıdaki kareye bakın

$a:$

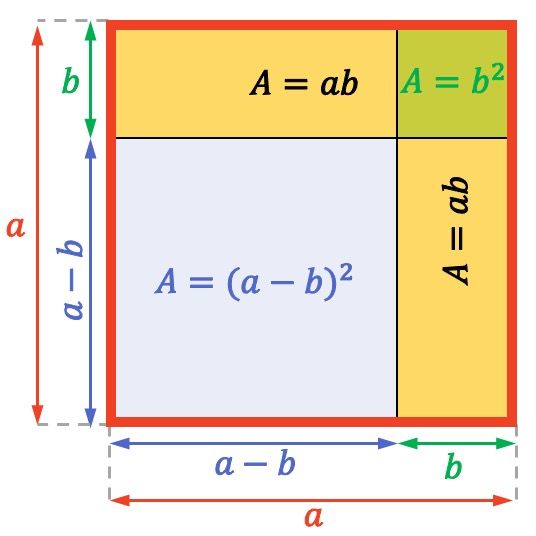
Bir karenin veya dikdörtgenin alanı (veya yüzey alanı), bitişik iki kenarının çarpılmasıyla hesaplanır. Bu nedenle yukarıdaki tamsayı karenin tamamının alanı

$a\cdot a = a^2.$

Benzer şekilde her sarı dikdörtgenin alanı eşittir

$a\cdot b = ab.$

Ve son olarak, sağ üstte gösterilen küçük karenin alanı

$b\cdot b =b^2.$

Bu, bir kenar karesi anlamına gelir

$(a-b),$

kimin yüzeyi

$(a-b)^2,$

bir kare boyut alanına ayrıştırılabilir

$a,$

boyutları olan bir dikdörtgenin alanının eksi 2 katı

$a$

$b$

artı bir yan karenin alanı

$b.$

Kısacası farkın karesi formülü geometrik olarak da doğrulanabilir:

$(a-b)^2=a^2-2ab+b^2$

Bir farkın karesi (veya çıkarma) ile ilgili çözülmüş problemler

Pratik yapabilmeniz için sizi farkın karesinin dikkate değer çarpımı üzerinde adım adım çözülen birkaç alıştırmayla baş başa bırakıyoruz. Aklınıza takılan tüm soruları aşağıya yorum olarak bize yazabileceğinizi unutmayın.

1. Egzersiz

Aşağıdaki çıkarma işlemlerinin karesini çözün:

$\text{A)} \ (x-2)^2$

$\text{B)} \ (3-7x)^2$

$\text{C)} \ \left(x^2-6\right)^2$

$\text{D)} \ (-3x+y)^2$

$\text{E)} \ (4x-3y)^2$

Çözüme bakın

Sorunun tüm dikkat çekici özdeşliklerini bulmak için, farkın karesi formülünü uygulamak yeterlidir:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}(x-2)^2& =x^2-2\cdot x\cdot 2 +2^2\\[2ex] & = \bm{x^2-4x +4}\end{aligned}$

$\text{B)} \ \begin{aligned}(3-7x)^2 & =3^2-2\cdot 3\cdot 7x +(7x)^2\\[2ex] & = \bm{9-42x+49x^2}\end{aligned}$

$\text{C)} \ \begin{aligned}\left(x^2-6\right)^2 & = \left(x^2\right)^2-2\cdot x^2\cdot 6 +6^2\\[2ex] & = \bm{x^4-12x^2 +36}\end{aligned}$

$\text{D)} \ \begin{aligned}(-3x+y)^2 & = (y-3x)^2 \\[2ex] & = y^2-2\cdot y\cdot 3x +(3x)^2\\[2ex] & = \bm{y^2-6yx+9x^2}\end{aligned}$

$\text{E)} \ \begin{aligned}(4x-3y)^2 & = (4x)^2-2\cdot 4x\cdot 3y +(3y)^2\\[2ex] & = \bm{16x^2-24xy+9y^2}\end{aligned}$

Alıştırma 2

Formülü uygulayarak iki miktarın farklarının aşağıdaki karelerini belirleyin:

$\text{A)} \ \left(6x^3-4y^4\right)^2$

$\text{B)} \ \displaystyle \left(\sqrt{2x}-\sqrt{8x}\right)^2$

$\text{C)} \ \displaystyle \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2$

Çözüme bakın

Sorunun tüm önemli ürünlerini belirlemek için kare çıkarma formülünü kullanmak gerekir:

$(a-b)^2=a^2-2ab+b^2$

$\text{A)} \ \begin{aligned}\left(6x^3-4y^4\right)^2 & =\left(6x^3\right)^2-2\cdot 6x^3\cdot 4y^4 +\left(4y^4\right)^2\\[2ex] & = \bm{36x^6-48x^3y^4+16y^8}\end{aligned}$

B) bölümünü çözmek için, eğer bir kökün karesi alınırsa basitleştirildiğini hatırlamanız gerekir:

$\text{B)} \ \begin{aligned}\left(\sqrt{2x}-\sqrt{8x}\right)^2 & =\left(\sqrt{2x}\right)^2-2\cdot \sqrt{2x}\cdot \sqrt{8x} +\left(\sqrt{8x}\right)^2\\[2ex] & =2x-2\sqrt{2x\cdot 8x} +8x \\[2ex] & = 10x-2\sqrt{16x^2} \\[2ex] &= 10x-2\cdot 4x = \\[2ex] & = 10x -8x \\[2ex] & = \bm{2x}\end{aligned}$

Son kare çıkarma işlemindeki monomların kesirli katsayıları vardır, bu nedenle bunu çözmek için kesirlerin özelliklerini kullanmamız gerekir:

$\text{C)} \ \displaystyle \begin{aligned} \left(\frac{5}{2}x^2-\frac{4}{5}x\right)^2 & = \left(\frac{5}{2}x^2\right)^2-2\cdot \frac{5}{2}x^2\cdot \frac{4}{5}x +\left(\frac{4}{5}x\right)^2\\[2ex] & = \frac{5^2}{2^2}x^4-2\cdot \frac{20}{10}x^3 +\frac{4^2}{5^2}x^2 \\[2ex] &= \frac{25}{4}x^4 -2\cdot 2x^3+\frac{16}{25}x^2 \\[2ex] & = \mathbf{\frac{25}{4}} \bm{x^4-4x^3+}\mathbf{\frac{16}{25}}\bm{x^2}\end{aligned}$

Bir farkın (veya çıkarmanın) karesi nedir?

Bir farkın karesi (veya çıkarma) formülü

Fark (veya çıkarma) karelerine örnekler

örnek 1

Örnek 2

Farkın karesi formülünün kanıtı

Bir farkın karesinin geometrik yorumu

Bir farkın karesi (veya çıkarma) ile ilgili çözülmüş problemler

1. Egzersiz

Alıştırma 2

Yorum bırakın Yanıtı iptal et