Bu sayfada bir çizgi ile bir daire arasındaki farklı göreceli konumlar açıklanmaktadır. Ayrıca bir çizgi ile bir daire arasındaki göreceli konumu nasıl bulacağınızı da görebileceksiniz.
Bir çizginin ve bir dairenin göreceli konumları nelerdir?
Analitik geometride, bir doğrunun bir daireye göre göreceli konumu yalnızca dış, teğet veya kesen olabilir:
- Dış : çizgi ile dairenin merkezi arasındaki mesafe yarıçaptan büyük olduğunda.
- Teğet : Doğru ile dairenin merkezi arasındaki mesafenin yarıçapa eşit olması.
- Secant : Doğru ile daire merkezi arasındaki mesafenin yarıçaptan küçük olması.
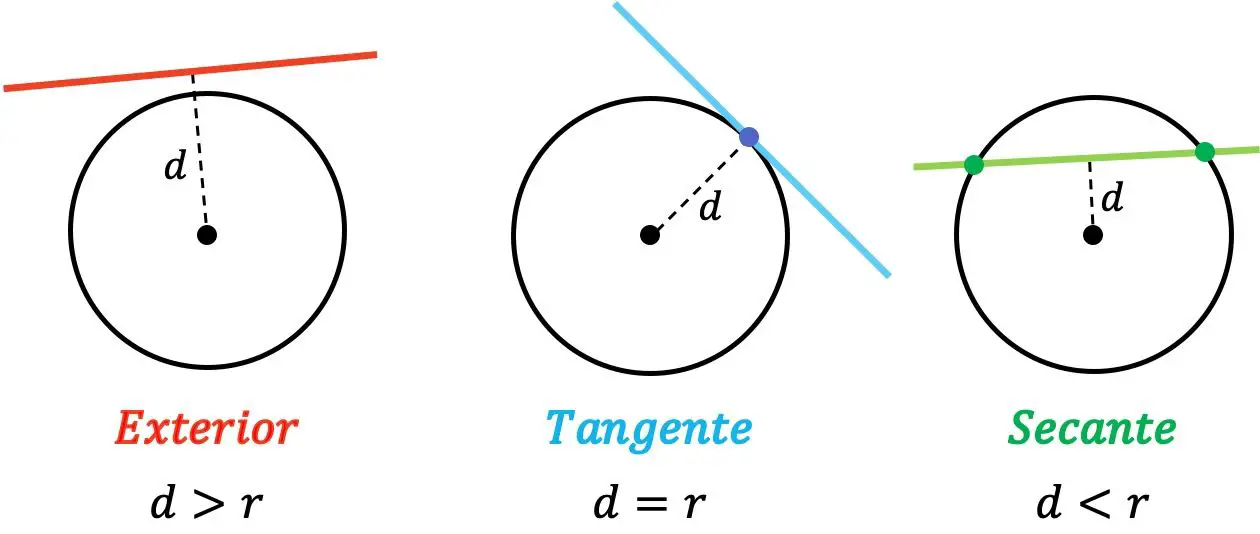
Yani bir doğru çemberin dışındaysa onu hiçbir noktada kesmez. Öte yandan doğru çembere teğet olduğunda ikisinin ortak bir noktası vardır. Ve son olarak, bir doğru, onu iki farklı noktada kestiğinde çembere kesen bir çizgidir.
Bir çizgi ile bir daire arasındaki göreceli konum nasıl belirlenir?
Bir doğrunun düzlemdeki bir daireye göre göreceli konumunu bulmanın iki yolu vardır: biri doğru ile dairenin merkezi arasındaki mesafeyi hesaplayarak, diğeri ise denklemin bileşik denklem sistemini çözerek. Çemberin doğrusu ve denklemi.
Daha sonra, her yöntemin tam olarak ne olduğunu göreceğiz.
Yöntem 1: Çizgi ile dairenin merkezi arasındaki mesafe
Bir doğru ile bir daire arasındaki göreli konum kavramının açıklanmasında gördüğümüz gibi, bir doğru ile bir dairenin merkezi arasındaki mesafe onun ne tür bir göreli konum olduğunu gösterir.
Dolayısıyla bu yöntem, çizgi ile dairenin merkezi arasındaki mesafeyi bulmayı içerir. Açıkçası, bunu yapabilmek için bir nokta ile bir çizgi arasındaki mesafeyi nasıl hesaplayacağınızı bilmeniz gerekir; bu sayfada bunun nasıl yapılacağını, örnekleri ve çözülmüş alıştırmaları görebilirsiniz.
Yani, elde edilen mesafenin sonucuna bağlı olarak, şu ya da bu durum olacaktır:
- Elde edilen mesafe dairenin yarıçapından büyükse çizgi dairenin dışında olacaktır.
- Elde edilen mesafe dairenin yarıçapına eşitse çizgi daireye teğet olacaktır.
- Elde edilen mesafe dairenin yarıçapından küçükse çizgi daireyi kesecektir.
Yöntem 2: Bir denklem sistemini çözün
Bir doğrunun bir daireye göre konumunu bulmanın bir başka yolu, doğrunun denklemi ve dairenin denkleminden oluşan bir denklem sistemi kullanmaktır. Açıkçası, bu yöntemi uygulamak için çevre denkleminin ne olduğunu ve çizgi denkleminin formülünün ne olduğunu bilmeniz gerekir.
Denklem sisteminin çözüm sayısına bağlı olarak şu veya bu durumla karşı karşıya kalacağız:
- Denklem sisteminin çözümü yoksa doğru ile dairenin ortak noktası yoktur, yani doğru dairenin dışındadır .
- Denklem sisteminin 1 çözümü varsa, bu, doğru ve dairenin ortak bir noktaya sahip olduğu, dolayısıyla doğrunun daireye teğet olduğu anlamına gelir.
- Denklem sisteminin 2 çözümü varsa, bu, doğru ve dairenin iki ortak noktasının olduğu anlamına gelir; dolayısıyla doğru, daireye keser .