▷ Çıkarma işleminin türevi (formül ve çözümlü alıştırmalar)

Bu makalede fonksiyonlarda çıkarma işleminin (formül) nasıl elde edileceğini açıklıyoruz. Ayrıca çıkarma türevlerinin örneklerini ve pratik yapmak için adım adım çözülmüş alıştırmaları bulacaksınız.

Bir çıkarma işleminin türevinin formülü

İki fonksiyonun çıkarılmasının türevi, her fonksiyonun türevinin ayrı ayrı çıkarılmasına eşittir.

$z(x)=f(x)-g(x) \quad\color{orange}\bm{\longrightarrow}\quad\color{black} z'(x)=f'(x)-g'(x)$

Yani iki fonksiyonun ayrı ayrı türevini alıp sonra çıkarmak, önce fonksiyonları çıkarıp sonra türev almakla eşdeğerdir.

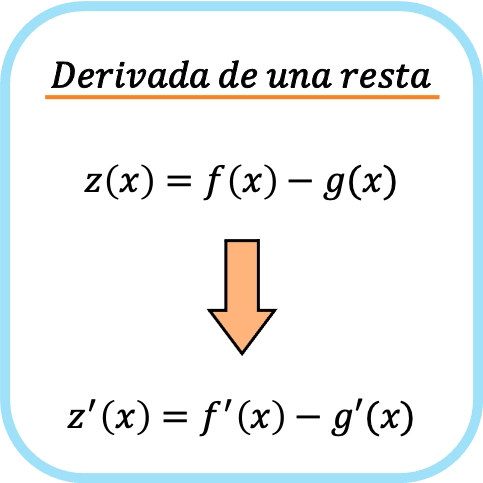
Benzer şekilde, aynı türev alma kuralı iki veya daha fazla fonksiyonun çıkarılması için de geçerlidir; yani üç, dört, beş,… fonksiyon çıkarmamız varsa, her birinin ayrı ayrı türevini almamız ve sonra bunları çıkarmamız gerekir.

$\begin{array}{c}z(x)=f(x)- g(x)- h(x)- \dots\\[1.5ex]\color{orange}\bm{\downarrow}\quad\color{black} \\[1.5ex]z'(x)=f'(x)-g'(x)- h'(x)- \dots\end{array}$

Gördüğünüz gibi fonksiyonların farkının türevinin formülü, toplamın türevi kuralına çok benzer.

➤ Bakınız: fonksiyonların toplamının türevi

Çıkarma işleminin türevi örnekleri

Bir çıkarma işleminin türevinin formülünün ne olduğunu gördükten sonra, fonksiyonlarda çıkarma işlemlerinin nasıl türetildiğini tam olarak anlamak için bu tür işlemlerin çeşitli türev örneklerini analiz etmeye geçiyoruz.

Örnek 1: Potansiyel fonksiyonların çıkarılmasının türevi

$f(x)=x^3-4x$

İki fonksiyonun çıkarılmasının türevi, her fonksiyonun ayrı ayrı türevlerinin farkına eşdeğerdir. Bu nedenle öncelikle her fonksiyonun türevini ayrı ayrı hesaplayacağız:

$\cfrac{d}{dx} \ x^3=3x^2$

$\cfrac{d}{dx}\ 4x=4$

Dolayısıyla tüm fonksiyonun türevi aşağıdaki gibidir:

$f'(x)=3x^2-4$

Örnek 2: Farklı fonksiyonlarda çıkarma işleminin türevi

$f(x)=\text{cos}(x)-\log_7(x^2)$

Çıkarma fonksiyonlarının türevini almak için önce iki fonksiyonun farklılığını ayrı ayrı almalı, sonra da çıkarmalısınız.

$\cfrac{d}{dx} \ \text{cos}(x)=-\text{sen}(x)$

$\cfrac{d}{dx}\ \log_7 (x^2)=\cfrac{2x}{x^2\cdot \ln(7)}=\cfrac{2}{x\ln(7)}$

Ve iki türevi yaptıktan sonra, bunları aynı başlangıç sırasıyla çıkarıyoruz:

$f'(x)=-\text{sen}(x)-\cfrac{2}{x\ln(7)}$

Örnek 3: Kareli çıkarma işleminin türevi

$f(x)=\left(x^7-2x^3-9\right)^2$

Bu durumda bileşik bir fonksiyonumuz var, çünkü bu üç kareli fonksiyon arasında bir çıkarma işlemidir. Bu nedenle, bir potansiyel fonksiyonun türevi formülünü ve tüm fonksiyonun türevini hesaplamak için zincir kuralını kullanmamız gerekir:

$f(x)=2\left(x^7-2x^3-9\right)\cdot \left(7x^6-6x^2\right)$