▷ Bir çarpımın türevi (formül ve çözülmüş alıştırmalar)

Bu yazıda iki fonksiyonun (formül) çarpımının nasıl elde edileceğini açıklıyoruz. Ek olarak, fonksiyonların çarpımlarının türevlerine ilişkin birçok örnek görebileceksiniz ve hatta çarpma türevleriyle ilgili çözülmüş alıştırmalar yapabileceksiniz.

Bir ürünün türevinin formülü

İki farklı fonksiyonun bir çarpımının türevi, birinci fonksiyonun türevinin ikinci farklılaşmamış fonksiyonla çarpımı artı birinci farklılaşmamış fonksiyonun ikinci fonksiyonun türeviyle çarpımına eşittir.

Başka bir deyişle, f(x) ve g(x) iki farklı fonksiyon ise, iki fonksiyonun çarpımının türevinin formülü aşağıdaki gibidir:

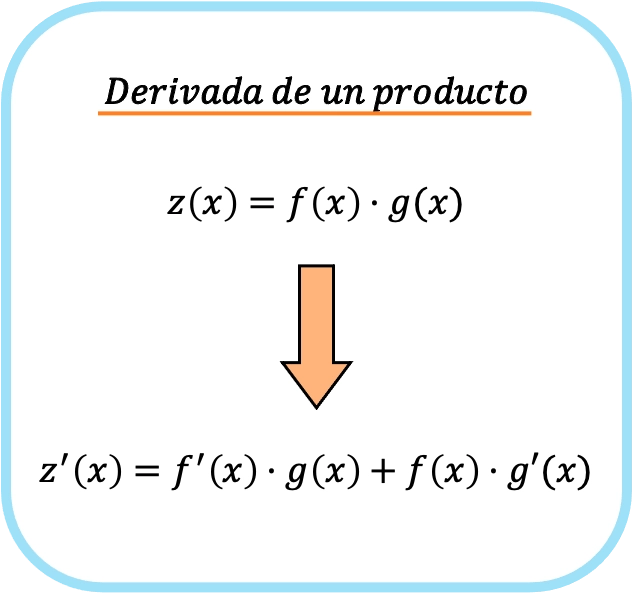
Böylece bir çarpımın türevi kuralını uygulayarak basit bir çarpmadan iki farklı çarpıma geçiyoruz.

Bir ürünün türevi örnekleri

Bir çarpımın (veya çarpımının) türevinin formülünün ne olduğunu öğrendikten sonra, bu türevin birkaç örneğini çözeceğiz. Bu, iki fonksiyonun çarpımının nasıl türetildiğini anlamanızı çok daha kolaylaştıracaktır.

örnek 1

Bu örnekte iki potansiyel fonksiyonun türevini çarparak çözeceğiz:

$f(x)=5x^2\cdot (x^3+4x-6)$

Önceki bölümde gördüğümüz gibi çarpmanın türevinin formülü şöyledir:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Bu nedenle öncelikle her fonksiyonun türevini ayrı ayrı hesaplamamız gerekir:

$\cfrac{d}{dx}\ 5x^2=10x$

$\cfrac{d}{dx}\ (x^3+4x-6)=3x^2+4$

Her fonksiyonun türevini bildiğimizde, iki fonksiyonun çarpımının türevinin formülünü uygulayabiliriz. Yani, birinci faktörün türevini, türevini almadan ikinci faktörle çarparız, ardından birinci faktörün çarpımını, ikinci faktörün türeviyle türevini almadan toplarız:

$\begin{array}{c}f(x)=5x^2\cdot (x^3+4x-6)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\end{array}$

Son olarak elde edilen sonucu basitleştirmek için işlemleri gerçekleştiriyoruz:

$\begin{aligned}f'(x)& =10x\cdot (x^3+4x-6)+5x^2\cdot (3x^2+4)\\[1.5ex] & = 10x^4+40x^2-60x +15x^4+20x^2 \\[1.5ex] & = 25x^4+60x^2-60x\end{aligned}$

Örnek 2

Bu durumda bir sabitin çarpımını bir fonksiyonla türeteceğiz:

$f(x)=7\cdot (x^2+3x)$

Bir çarpımın türev kuralı aşağıdaki gibidir:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Böylece, ürünün parçası olan her fonksiyonu ayrı ayrı türetiyoruz:

$\cfrac{d}{dx}\ 7=0$

$\cfrac{d}{dx}\ (x^2+3x)=2x+3$

Daha sonra çarpma işleminin türevine ilişkin kuralı uygularız:

$\begin{array}{c}f(x)=7\cdot (x^2+3x)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=0\cdot (x^2+3x)+7\cdot (2x+3)=14x+21\end{array}$

Bir sabitin türevinin her zaman sıfır olduğuna dikkat edin, dolayısıyla bir sabiti bir fonksiyonla çarpmanın türevinin, sabitin ve fonksiyonun türevinin çarpımına eşit olduğu sonucunu çıkarabiliriz.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=k\cdot f(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=k\cdot f'(x)\end{array} \end{empheq}$

Örnek 3

Üstel fonksiyon ile doğal logaritma arasındaki çarpımı çözelim:

$f(x)=4^{3x}\cdot \ln(x^2)$

İki fonksiyonun çarpımının türevinin formülü şöyledir:

$\begin{array}{c}z(x)=f(x)\cdot g(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x)\end{array}$

Bu nedenle öncelikle aşağıdaki gibi ürünü oluşturan her fonksiyonun türevini ayrı ayrı yapmalıyız:

$\cfrac{d}{dx}\ 4^{3x}=4^{3x}\cdot \ln (4) \cdot 3$

$\cfrac{d}{dx}\ \ln(x^2)=\cfrac{2x}{x^2}=\cfrac{2}{x}$

Dolayısıyla fonksiyonların türetilmiş çarpımı şu şekildedir:

$\begin{array}{c}f(x)=4^{3x}\cdot \ln(x^2)\\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] f'(x)=4^{3x}\cdot \ln (4) \cdot 3\cdot \ln(x^2) +4^{3x}\cdot \cfrac{2}{x} \end{array}$

Bir çarpımın türevine ilişkin çözülmüş alıştırmalar

Aşağıdaki fonksiyon ürünlerini türetir:

$\text{A) }f(x)=5\ln(3x)$

$\text{B) }f(x)=(4x^2+1)(6x^3-7)$

$\text{C) }f(x)=\text{cos}(4x)\cdot e^{x^2}$

$\text{D) }f(x)=(3x^3-4x^2+8x)\cdot \sqrt{6x^2+3x}$

$\text{E) }f(x)=5^{4x}\cdot \log_9(x^3-x)$

$\text{F) }f(x)=\left(10x^6-6x^5\right)^4\cdot \text{arcsen}(x^2+9x)$

Çözümü görün

$\text{A) } f'(x)=5\cdot \cfrac{3}{3x} =\cfrac{5}{x}$

$\begin{aligned}\text{B) }f'(x)&=8x\cdot (6x^3-7)+(4x^2+1)\cdot 18x^2\\[1.2ex]&=48x^4-56x+72x^4+18x^2\\[1.2ex]&=120x^4+18x^2-56x \end{aligned}$

$\text{C) }f'(x) =-4\text{sen}(4x)\cdot e^{x^2}+\text{cos}(4x)\cdot e^{x^2}\cdot 2x$

$\text{D) }f'(x)=(9x^2-8x+8)\cdot \sqrt{6x^2+3x}+(3x^3-4x^2+8x)\cdot\cfrac{12x+3}{2\sqrt{6x^2+3x}}$

$\text{E) }f'(x)=5^{4x}\cdot \ln(5) \cdot 4 \cdot \log_9(x^3-x)+ 5^{4x}\cdot\cfrac{3x^2-1}{(x^3-x)\ln(9)}$

$\begin{aligned}\text{F) }f'(x)=& 4\left(10x^6-6x^5\right)^3\cdot (60x^5-30x^4)\cdot \text{arcsen}(x^2+9x)\ +\\[1.2ex] &+\left(10x^6-6x^5\right)^4\cdot \cfrac{2x+9}{\sqrt{1-\left(x^2+9x\right)^2}}\end{aligned}$

Üç işlevli bir üründen türetilmiştir

Daha sonra, 2 fonksiyonunkine çok benzediğinden ve bazı durumlarda yararlı olabileceğinden, sizi 3 fonksiyonun çarpımının türevi formülüyle bırakıyoruz.

Üç fonksiyonun bir çarpımının türevi, birinci fonksiyonun ve diğer iki fonksiyonun türevinin çarpımına, artı ikinci fonksiyonun ve diğer iki fonksiyonun türevinin çarpımına, artı üçüncü fonksiyonun türevinin çarpımına eşittir. üçüncü fonksiyon.diğer iki fonksiyon tarafından fonksiyon.

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=1mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} \begin{array}{c}z(x)=f(x)\cdot g(x)\cdot h(x) \\[1.5ex]\color{orange}\bm{\downarrow}\\[1.5ex] z'(x)=f'(x)\cdot g(x)\cdot h(x)+f(x)\cdot g'(x)\cdot h(x)+f(x)\cdot g(x)\cdot h'(x)\end{array} \end{empheq}$

Örneğin, üç farklı fonksiyonun aşağıdaki çarpımını elde etmek istiyorsak:

$f(x)=3x\cdot e^{2x} \cdot \text{sen}(x)$

Türevi çözmek için üç fonksiyonun çarpımının türevi kuralını uygulamamız gerekir, dolayısıyla:

$f'(x)=3\cdot e^{2x} \cdot \text{sen}(x)+3x\cdot 2e^{2x} \cdot \text{sen}(x)+3x\cdot e^{2x} \cdot \text{cos}(x)$

Bir ürünün türevinin formülünün gösterilmesi

Son olarak bir çarpımın türevinin formülünü göstereceğiz. Ezberlemenize gerek yok ama formüllerin nereden geldiğini anlamak her zaman iyidir. 🙂

Türevin matematiksel tanımından:

$\displaystyle f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

z fonksiyonu iki farklı fonksiyonun çarpımı olsun:

$z(x)=f(x)\cdot g(x)$

O zaman tanıma göre z’nin türevi şöyle olacaktır:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{\bigl[f(x+h)\cdot g(x+h)\bigr]-\bigl[f(x)\cdot g(x)\bigr]}{h}$

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x)\cdot g(x)}{h}$

Bildiğimiz gibi bir terimi toplayıp çıkararak eklersek, ikisi de aynı terim olduğu sürece bu sonucu etkilemez. Bu nedenle bir sonraki adıma geçebiliriz:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)\color{orange}\bm{-f(x+h)\cdot g(x)+f(x+h)\cdot g(x)}\color{black}-f(x)\cdot g(x)}{h}$

Şimdi önceki sınırı iki farklı sınıra ayırmak için sınır özelliklerini kullanıyoruz:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\cdot g(x+h)-f(x+h)\cdot g(x)}{h}+\lim_{h \to 0}\frac{f(x+h)\cdot g(x)-f(x)\cdot g(x)}{h}$

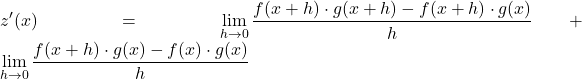
İki kesrin payındaki ortak faktörü çıkarıyoruz:

$\displaystyle z'(x)=\lim_{h \to 0}\frac{f(x+h)\bigl(g(x+h)-g(x)\bigr)}{h}+\lim_{h \to 0}\frac{g(x)\bigl(f(x+h)-f(x)\bigr)}{h}$

Öte yandan aşağıdaki limitin sonucunu biliyoruz:

$\displaystyle \lim_{h \to 0}f(x+h)=f(x)$

Bu nedenle limitleri basitleştirebiliriz:

$\displaystyle z'(x)=\lim_{h \to 0}f(x+h)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+\lim_{h \to 0}g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

$\displaystyle z'(x)=f(x)\lim_{h \to 0}\frac{g(x+h)-g(x)}{h}+g(x)\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}$

Son olarak, kalan iki limite bakıldığında her biri bir fonksiyonun türevinin tanımına karşılık gelir. Bu nedenle eşitlik basitleştirilebilir:

$\displaystyle z'(x)=f(x)\cdot g'(x)+g(x)\cdot f'(x)$

Veya eşdeğer:

$\definecolor{taronjaquadreejemplo}{HTML}{FF9800} \newtcbox{\mymath}[1][]{% nobeforeafter, math upper, tcbox raise base, enhanced, colframe=taronjaquadreejemplo, boxrule=1.1pt, boxsep=2mm, #1} \begin{empheq}[box={\mymath[colback=white, shadow={2mm}{-2mm}{0mm}{taronjaquadreejemplo!20!white,} ]}]{equation*} z'(x)=f'(x)\cdot g(x)+f(x)\cdot g'(x) \end{empheq}$

Bir çarpımın türevi (veya çarpımı)

Bir ürünün türevinin formülü

Bir ürünün türevi örnekleri

örnek 1

Örnek 2

Örnek 3

Bir çarpımın türevine ilişkin çözülmüş alıştırmalar

Üç işlevli bir üründen türetilmiştir

Bir ürünün türevinin formülünün gösterilmesi

Yorum bırakın Yanıtı iptal et