Belirsizlik türleri (belirsiz sınırlar)

Bu yazımızda belirsizliğin ne olduğunu açıklıyoruz. Her türlü belirsizliğin ne olduğunu ve bunları nasıl çözebileceğinizi keşfedeceksiniz. Ayrıca tüm belirsizliklerin fonksiyon limitleri üzerinde adım adım çözülen alıştırmaları görebileceksiniz.

Belirsizlikler nelerdir?

Belirsiz formlar olarak da adlandırılan belirsizlikler, sonucu tanımlanmayan fonksiyonların limitlerinin hesaplanmasında ortaya çıkan matematiksel ifadelerdir. Bu nedenle limitlerdeki belirsizliklerin giderilmesi için fonksiyonun türüne göre bir ön prosedür uygulanması gerekmektedir.

Yani belirsizlikle karşılaştığımızda bu, limitin olmadığı veya çözülemeyeceği anlamına gelmez, aksine limitin çözümünü bulmak için fonksiyonda değişiklik yapmamız gerektiği anlamına gelir.

Belirsizlik türleri

Belirsizlikler veya belirsiz formlar aşağıdaki türlere ayrılır:

  • Belirsizlik sonsuzluk eksi sonsuzluk (∞-∞)
  • Sıfır arasındaki belirsizlik sayısı (k/∞)
  • Sıfır arasında sıfır belirsizlik (0/0)
  • Sonsuz (∞/∞) arasındaki sonsuz belirsizlik
  • Belirsizlik 1 sonsuza yükseltilmiş (1 ∞ )
  • Sıfır belirsizliği sıfıra yükseltildi (0 0 )
  • Sonsuz için sıfır belirsizlik (0·∞)
  • Sonsuza yükseltilmiş sıfır belirsizlik (0 ∞ )
  • Sonsuz belirsizlik sıfıra getirildi (∞ 0 )

Daha sonra her türlü belirsizliği nasıl çözeceğimizi göreceğiz.

Sonsuz eksi sonsuz belirsizlik

Belirsiz formdaki sonsuz eksi sonsuz sıfıra eşit değildir, çünkü çok büyük iki sayıyı çıkarıyoruz ama hangisinin daha büyük olduğunu bilmiyoruz. Bu nedenle sonsuzlukların farkının sonucu her sonsuzluğun sırasına bağlıdır.

\infty-\infty

Bu tür belirsizliği çözmek kolay değildir çünkü işlevin türüne bağlı olarak şu veya bu prosedürün uygulanması gerekir. Bu nedenle açıklamanın tamamını aşağıdaki bağlantıdan görüntülemenizi öneririz:

➤ Bakınız: belirsizlik sonsuz eksi sonsuzluk nasıl çözülür

Sıfır arasındaki belirsizlik sayısı

Bir sabitin sıfıra bölünmesinin belirsizliği, rasyonel bir fonksiyonun paydası iptal edildiğinde elde edilir.

\cfrac{k}{0}

Bu tür belirsiz formun sonucu her zaman daha sonsuz, daha az sonsuz olacaktır veya fonksiyonun limiti olmayacaktır. Örnek olarak bir limit çözerek bu belirsizliğin nasıl hesaplandığını görelim:

\displaystyle\lim_{x\to 0}\cfrac{-4}{x^2}=\cfrac{-4}{0^2}=\cfrac{-4}{0}=\infty

Bir sayının sıfıra bölünmesinin belirsizliğini elde ettik, dolayısıyla fonksiyonun yanal limitlerini hesaplamamız gerekiyor:

\displaystyle\lim_{x\to 0^-}\cfrac{-4}{0^2}=\cfrac{-4}{(-0,001)^2}=\cfrac{-4}{+0}=-\infty

\displaystyle\lim_{x\to 0^+}\cfrac{-4}{0^2}=\cfrac{-4}{0,001^2}=\cfrac{-4}{+0}=-\infty

➤ Bakınız: yanal sınırlar nelerdir?

Fonksiyonun iki yanal limiti aynı sonucu verir, yani tanım gereği fonksiyonun x 0’a yaklaştığında limiti eksi sonsuzluğu verir:

\displaystyle\lim_{x\to 0^-}f(x)=\lim_{x\to 0^+}f(x)=-\infty \ \longrightarrow \ \lim_{x\to 0}f(x)=-\infty

Yanal limitler farklı değerler vermiş olsaydı fonksiyonun bu noktadaki limitinin olmayacağını unutmayın.

Sıfır belirsizlik arasında sıfır

Belirsiz limit sıfırın sıfıra bölümü çok yaygındır ve pay ve paydanın birbirini götürdüğü kesirli fonksiyonlarda elde edilir.

\cfrac{0}{0}

Bu tür belirsiz limit, fonksiyona bağlı olarak farklı şekilde çözümlenir. Örneğin fonksiyonun kökleri varsa farklı adımların gerçekleştirilmesi gerekir. Bu tür belirsizliğin farklı çözümlerini aşağıdaki bağlantıda görebilirsiniz:

➤ Bakınız: sıfır arasındaki sıfır belirsizliğinin nasıl çözüleceği

Sonsuz arasında sonsuz belirsizlik

Sonsuzluk arasındaki sonsuz belirsizlik genellikle kesirli fonksiyonların sonsuz limitlerinde ortaya çıkar. Belirsizlik iki sonsuzluğun bölümü olmasına rağmen sonucun mutlaka sonsuz olması gerekmez.

\cfrac{\infty}{\infty}

Bu tür belirsiz formlar karşılaştırma yoluyla çözümlenir. Yani payın derecesi ve paydanın derecesi gözlemlenir ve hangisinin büyük olduğuna bağlı olarak limit sonucu biri veya diğeri olur. Tüm vakaları aşağıdaki bağlantıda görebilirsiniz:

➤ Bakınız: sonsuzluk arasındaki sonsuz sınırlara ilişkin çözümlü alıştırmalar

Belirsizlik 1 sonsuza yükseltildi

Matematiksel olarak 1’in her kuvveti 1’e eşit olduğundan 1’den sonsuza 1’in verildiği düşünülebilir. Ancak bu terim bir belirsizliktir ve dolayısıyla sonucu o kadar kolay çıkarılamaz.

1^{\infty}

Bu tür belirsizlik aşağıdaki formül uygulanarak hesaplanır:

\displaystyle\lim_{x\to+\infty}f(x)^{g(x)}=\lim_{x\to+\infty}e^{g(x)\cdot [f(x)-1]}

Örneğin aşağıdaki limit sonsuzluğun kuvvetini verdiği için belirsizdir:

\displaystyle\lim_{x\to+\infty}\left(1-\frac{1}{x}\right)^x=\left(1-\frac{1}{+\infty}\right)^{+\infty}=(1-0)^{+\infty}=1^{+\infty}

Bu nedenle bu tür belirsizlik için formülü kullanmalıyız:

\displaystyle\lim_{x\to+\infty}e^{x\cdot\left[1-\frac{1}{x}-1\right]}=\lim_{x\to+\infty}e^{x\cdot\left[-\frac{1}{x}\right]}=\lim_{x\to+\infty}e^{-1}=\frac{1}{e}

Ve böylece sonsuza yükseltilmiş belirsiz sınırı zaten çözmüş olduk.

Sıfır belirsizlik sıfıra getirildi

Sıfır kuvvete karşı sıfır belirsizlik, karmaşık fonksiyonların sınırları dahilinde görünür.

0^0

Bu tür belirsiz limiti çözmek için aşağıdaki limit özelliğini kullanmanız gerekir:

\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}

Örneğin, aşağıdaki limit 0 üzeri 0’ın belirsiz formunu verir:

\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=\left(\frac{1}{+\infty}\right)^{\frac{1}{+\infty}}=0^0

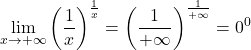
Ancak limite logaritma uygularsak değerini bulabiliriz:

\begin{array}{l}\displaystyle\lim_{x\to +\infty}\left(\frac{1}{x}\right)^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln\left(\frac{1}{x}\right)}}=\\[5ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln\left(\frac{1}{x}\right)}{x}}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln1-\ln x}{x}}}=\\[5ex]=\displaystyle e^{^{\displaystyle\lim_{x\to +\infty}\frac{-\ln x}{x}}}=e^{^{\displaystyle\frac{-\infty}{+\infty}}}=e^0=1\end{array}

Sonsuzluk için sıfır belirsizlik

Sıfır ile sonsuzun çarpımının belirsizliğiyle karşılaşmak zordur ancak bu, onu belirlemenin kolay olduğu anlamına gelmez.

0\cdot \infty

Bu tür belirsizliği çözmenin tek bir yöntemi yoktur ancak bu, fonksiyonun türüne bağlıdır. Bu durumda fonksiyonu sonsuz belirsizliğe bölü sonsuz veya sıfır belirsizliğini sıfıra bölerek her bir belirsizlik için yukarıda gördüğümüz çözüm yöntemlerini uygulamamız gerekir.

Yani eğer bir fonksiyonun limiti 0 ve diğer fonksiyonun limiti ∞ ise:

\displaystyle\lim_{x\to a}f(x)=0\qquad\lim_{x\to a}g(x)=\infty

Aşağıdaki değişiklikleri yaparak bu türü süresiz olarak dönüştürebiliriz:

\displaystyle\lim_{x\to a}f(x)\cdot g(x)\begin{cases}\displaystyle\lim_{x\to a}\frac{f(x)}{\displaystyle\frac{1}{g(x)}}=\frac{0}{0}\\[10ex]\displaystyle\lim_{x\to a}\frac{g(x)}{\displaystyle\frac{1}{f(x)}}=\frac{\infty}{\infty}\end{cases}

Örnek olarak belirsiz bir limiti çözerek bunu nasıl yapacağımızı görelim:

\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=e^{-\infty}\cdot (+\infty)=0\cdot \infty

Sonsuz üzerinde sonsuz belirsizlik elde etmek için fonksiyon üzerinde çalışırız, sonra limiti buluruz:

\begin{array}{l}\displaystyle\lim_{x\to +\infty}e^{-x}\cdot x=\lim_{x\to +\infty}\frac{x}{\displaystyle\frac{1}{e^{-x}}}=\\[6ex]=\displaystyle \lim_{x\to +\infty}\frac{x}{e^x}=\frac{+\infty}{e^{+\infty}}=\frac{+\infty}{+\infty}=0\end{array}

Sonsuza yükseltilmiş sıfır belirsizlik

Sonsuza yükseltilmiş belirsizlik sıfırını anlamak biraz zordur çünkü çok küçük bir sayıyı çok büyük bir sayıya yükseltiyoruz.

0^{\infty}

Bu belirsiz formlar elde edildiğinde aşağıdaki formülün kullanılması gerekir:

\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}

Bu tür belirsizliğin nasıl hesaplanacağını daha iyi anlamak için bir örnek çözelim:

\begin{array}{l}\displaystyle\lim_{x\to 0^+}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to 0^+}\frac{1}{x}\cdot \ln(x)}}=\\[3.5ex]\displaystyle =e^{^{\displaystyle\frac{1}{0^+}\cdot \ln(0^+)}}=e^{+\infty\cdot (-\infty)}\\[3ex]\displaystyle =e^{-\infty}=\frac{1}{e^{+\infty}}=0\end{array}

Sonsuz belirsizlik sıfıra getirildi

Normalde sıfıra yükseltilen herhangi bir kuvvet 1 verir, ancak sıfıra yükseltilen sonsuzluğun belirsizliği mutlaka bu şekilde olmak zorunda değildir.

\infty^0

Sıfırın sıfıra yükseltildiği ve sıfırın sonsuza yükseltildiği belirsizliklerde olduğu gibi, bu tür belirsiz limiti çözmek için logaritmaların uygulanması gerekir:

\displaystyle\lim_{x\to a}f(x)^{g(x)}=e^{^{\displaystyle\lim_{x\to a}g(x)\cdot \ln\bigl(f(x)\bigr)}}

Bu tür belirsiz limitlerin nasıl çözüldüğünü adım adım bir örnek hesaplayarak görelim:

\begin{array}{l}\displaystyle\lim_{x\to +\infty}x^{\frac{1}{x}}=e^{^{\displaystyle\lim_{x\to +\infty}\frac{1}{x}\cdot \ln(x)}}=\\[3ex]\displaystyle =e^{^{\displaystyle\lim_{x\to +\infty}\frac{\ln(x)}{x}}}=e^{^{\displaystyle\frac{\ln(+\infty)}{+\infty}}}=\\[3ex]\displaystyle =e^{^{\displaystyle\frac{+\infty}{+\infty}}}=e^0=1\end{array}

Yorum bırakın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir

Scroll to Top