Belirsizlik sonsuz eksi sonsuz (∞-∞)

Bu yazıda sonsuz eksi sonsuz (∞-∞) belirsizliğinin nasıl çözüleceğini açıklıyoruz. Bu belirsizliğin farklı fonksiyon türleriyle örneklerini bulacaksınız ve ayrıca sonsuz eksi sonsuz belirsizlik adım adım çözülen alıştırmalarla pratik yapabileceksiniz.

Belirsizliği çözme sonsuz eksi sonsuz

Bir fonksiyonun limiti sonsuz eksi sonsuz veriyorsa, bu onun bir belirsizlik (veya belirsiz bir form) olduğu anlamına gelir. Yani belirsizlik eksi sonsuz veren bir fonksiyonun limiti doğrudan hesap yapılarak belirlenemez, bunun yerine bir ön işlem yapılması gerekir.

Bu nedenle sonsuz eksi sonsuz belirsizliği çözmek için öncelikle fonksiyonun türüne bağlı bir prosedür uygulamamız gerekir: polinom fonksiyon ise karşılaştırma yoluyla hesaplanabilir, rasyonel fonksiyon ise kesirlerin indirgenmesi gerekir ortak bir paydadır ve eğer irrasyonel bir fonksiyon ise eşleniği ile çarpılmalıdır.

$\displaystyle\lim_{x\to+\infty}\Bigl(f(x)-g(x)\Bigr)=\infty-\infty$

Daha sonra, sonsuz eksi sonsuz belirsizliğinin her fonksiyon tipinde nasıl çözüldüğünü örneklerle göreceğiz.

Polinom fonksiyonlarda sonsuz eksi sonsuz belirsizlik

Bir polinomda, belirsizlik sonsuzluğu eksi sonsuz, en yüksek dereceli sonsuza eşittir, yani en yüksek dereceli terim, sonsuzluğun pozitif veya negatif işaretini belirler.

Örneğin, sonsuz eksi sonsuzun belirsiz biçimini veren aşağıdaki polinom fonksiyonunun limitine bakın:

$\displaystyle\lim_{x\to+\infty}\bigl(x^2-3x\bigr)=(+\infty)^2-3\cdot (\infty)=+\infty-\infty=+\infty$

Bu durumda x ² terimi ikinci dereceden, 3x terimi ise birinci derecedendir, yani tek terimli x ² daha yüksek mertebeden olduğundan baskındır. Dolayısıyla bu terimden elde edilen limitin sonucu sonsuzdur.

Şu diğer örneklere bir göz atın:

$\begin{array}{l}\displaystyle\lim_{x\to+\infty}\bigl(x^5-4x^2-3x\bigr)=(+\infty)^5=+\infty\\[5ex]\displaystyle\lim_{x\to-\infty}\bigl(-3x^2-5x\bigr)=-3\cdot (-\infty)^2=-3\cdot \infty=-\infty\\[5ex]\displaystyle\lim_{x\to+\infty}\bigl(x^7-5x^4+x^3-2x-10\bigr)=(+\infty)^7=+\infty\end{array}$

Kısacası, polinom fonksiyonlarında sonsuza sınırlama yaptığımızda , diğer tüm terimleri göz ardı ederek, en yüksek dereceli terimin yerine sonsuzluğu koymalıyız .

Kesirlerde belirsizlik sonsuz eksi sonsuz

Cebirsel kesirlerin toplanmasında veya çıkarılmasında sonsuz eksi sonsuz belirsizliği oluştuğunda , önce kesirlerde toplama veya çıkarma işlemi yapmamız ve ardından limiti hesaplamamız gerekir.

Bir örneği adım adım çözerek kesirli bir fonksiyonda belirsizlik sonsuz eksi sonsuzun nasıl hesaplanacağını görelim:

$\displaystyle \lim_{x \to +\infty} \left( \frac{x^2}{x-1} - \frac{x}{3}\right)$

Önce limiti hesaplamaya çalışalım:

$\displaystyle \lim_{x \to +\infty}\left( \frac{x^2}{x-1} - \frac{x}{3}\right) = \frac{(+\infty)^2}{(+\infty)-1} - \frac{+\infty}{3} = \bm{+\infty - \infty}$

Ancak ∞-∞ belirsizliğini elde ederiz.

O halde öncelikle kesirlerde çıkarma işlemi yapmamız gerekiyor. Bunu yapmak için kesirleri ortak bir paydaya indiririz, yani bir kesirin payını ve paydasını diğerinin paydasıyla çarparız:

$\begin{array}{l}\displaystyle\lim_{x \to +\infty} \left( \frac{x^2}{x-1}-\frac{x}{3}\right)=\\[5ex]\displaystyle =\lim_{x \to +\infty}\left(\frac{x^2 \cdot 3}{(x-1)\cdot 3}- \frac{x\cdot (x-1)}{3\cdot (x-1)} \right)=\\[5ex]\displaystyle = \lim_{x \to +\infty} \left( \frac{3x^2 }{3(x-1)}- \frac{x^2-x}{3(x-1)}\right)\end{array}$

Artık her iki kesir de aynı paydaya sahip olduğuna göre bunları tek bir kesirde birleştirebiliriz:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -(x^2-x)}{3(x-1)}$

Pay ve paydada işlem yapıyoruz:

$\displaystyle \lim_{x \to +\infty} \frac{3x^2 -x^2+x}{3x-3} = \lim_{x \to +\infty} \frac{2x^2+x}{3x-3}$

Ve son olarak limiti tekrar hesaplıyoruz:

$\displaystyle \lim_{x \to +\infty}\frac{2x^2+x}{3x-3}=\frac{+\infty}{+\infty}=\bm{+\infty}$

Bu durumda sonsuzluk arasındaki sonsuz belirsizlik +∞ verir çünkü payın derecesi paydanın derecesinden büyüktür.

➤ Bakınız: sonsuzluk arasındaki sonsuzluk nedir?

belirsizlik sonsuz eksi köklerle sonsuz

Radikal toplama veya çıkarma işleminde belirsizlik sonsuzluk eksi sonsuzluk oluştuğunda , önce fonksiyonu eşlenik radikal ifadeyle çarpmalı ve bölmeli, sonra limiti çözmeliyiz.

Adım adım bir örnek kullanarak irrasyonel bir fonksiyonda sonsuz eksi sonsuz belirsizliğini nasıl çözeceğimizi göreceğiz:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)$

Önce fonksiyonun limitini radikallerle çözmeye çalışalım:

$\displaystyle\lim_{x\to +\infty}\left(x-\sqrt{x^2-5}\right)=+\infty-\sqrt{(+\infty)^2}=\bm{+\infty-\infty}$

Ancak ∞-∞ belirsiz formunu elde ederiz. Dolayısıyla sonsuz eksi sonsuzun ne kadar belirsizlik olduğunu bilmek için açıklanan prosedürü uygulamamız gerekir.

Fonksiyonun kökleri olduğundan, fonksiyonun tamamını birleşik irrasyonel ifadeyle çarpar ve böleriz:

$\displaystyle\lim_{x \to +\infty}\left(x-\sqrt{x^2-5}\right)= \lim_{x \to +\infty}\frac{\left(x-\sqrt{x^2-5}\right)\cdot\left(x+\sqrt{x^2-5}\right)}{x+\sqrt{x^2-5}}$

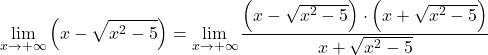
Payın cebirsel ifadesi, bir toplamın bir farkla çarpımının dikkate değer özdeşliğine karşılık gelir; bu nedenle ifadeyi basitleştirebiliriz:

$\displaystyle \lim_{x \to +\infty} \cfrac{\left(x-\sqrt{x^2-5}\right) \cdot \left(x + \sqrt{x^2-5}\right)}{ x + \sqrt{x^2-5}}= \lim_{x \to +\infty} \cfrac{x^2- \left( \sqrt{x^2-5}\right)^2}{ x + \sqrt{x^2-5}}$

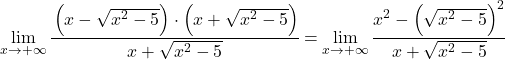
Artık limitin kökünü basitleştiriyoruz çünkü karesi alınmış durumda:

$\displaystyle \lim_{x \to +\infty}\frac{x^2-(x^2-5)}{x+\sqrt{x^2-5}}$

Kesirin payı üzerinde işlem yapıyoruz:

$\displaystyle \lim_{x \to +\infty} \frac{x^2- x^2+5}{x+\sqrt{x^2-5}}$

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}$

Ve son olarak limit hesaplamasını yeniden yapıyoruz:

$\displaystyle \lim_{x \to +\infty} \frac{5}{x+\sqrt{x^2-5}}=\frac{5}{+\infty+\sqrt{(+\infty)^2}}=\frac{5}{+\infty}=\bm{0}$

Dolayısıyla limitin sonucu 0’dır çünkü her sayının sonsuza bölümü sıfıra eşittir.

Sonsuz eksi sonsuz belirsizlik problemlerini çözdüm

1. Egzersiz

x artı sonsuza yaklaşırken aşağıdaki limiti çözün:

$\displaystyle\lim_{x\to +\infty}(7x^2-2x^3)$

Çözüme bakın

Bu limitte en yüksek mertebeden terim üçüncü dereceden olduğundan bu terimden elde edilen sonsuzluğa odaklanıyoruz.

$\displaystyle\lim_{x\to +\infty}(+7x^2-2x^3)=+\infty^2-\infty^3=+\infty-\infty=\bm{-\infty}$

Alıştırma 2

x negatif sonsuza yaklaşırken aşağıdaki polinom fonksiyonunun limitini hesaplayın:

$\displaystyle\lim_{x\to -\infty}(-5x^3-9x^2)$

Çözüme bakın

Negatif sonsuz küp negatif kalır, ancak karesi alındığında pozitif olur. daha sonra işaretleri önlerindeki katsayılar tarafından değiştirilse de:

$\begin{array}{l}\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\\[3ex]=-5(-\infty)^3-9(-\infty)^2=\\[3ex]=-5\cdot (-\infty)-9\cdot \infty=\\[3ex]=+\infty-\infty\end{array}$

Daha sonra, sonsuz eksi sonsuz şeklindeki belirsiz form, pozitif sonsuzluğu elde ettiğimiz en yüksek terim ( ^-5×3 ) ile tanımlanır:

$\displaystyle\lim_{x\to -\infty}(-5x^3+x^2)=\bm{+\infty}$

Alıştırma 3

Aşağıdaki rasyonel fonksiyonun sonsuzluğa olan sınırını belirleyin:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)$

Çözüme bakın

Öncelikle fonksiyondaki sonsuzluğu değiştirerek limiti hesaplamaya çalışıyoruz:

$\displaystyle\lim_{x\to +\infty}\left(\frac{x^3+1}{x-1}-\frac{x}{4}\right)=\frac{(+\infty)^3+1}{+\infty-1}-\frac{+\infty}{4} = \bm{+\infty -\infty}$

Ama sonuçta ∞ – ∞ belirsizliğiyle karşılaşıyoruz. Bu nedenle kesirleri ortak bir paydaya indiriyoruz:

$\begin{array}{l}\displaystyle\lim\limits_{x \to +\infty} \left(\frac{x^3+1}{x-1}-\frac{x}{4} \right)=\\[5ex]\displaystyle = \lim_{x\to +\infty}\left(\frac{(x^3+1)\cdot4}{(x-1)\cdot4}-\frac{x\cdot(x-1)}{4\cdot (x-1)}\right)=\\[5ex]\displaystyle =\lim_{x\to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)\end{array}$

Artık her iki kesir de aynı paydaya sahip olduğundan, bunları tek bir kesirde birleştirebiliriz:

$\displaystyle\lim_{x \to +\infty}\left(\frac{4x^3+4}{4x-4}-\frac{x^2-x}{4x-4}\right)=\lim_{x\to +\infty}\frac{4x^3+4-(x^2-x)}{4x-4}$

Payın parantezlerini yapıyoruz:

$\displaystyle\lim_{x \to +\infty} \frac{4x^3+4-x^2+x}{4x-4}$

Ve son olarak limiti belirliyoruz:

$\displaystyle\lim_{x \to +\infty}\frac{4x^3+4-x^2+x}{4x-4}=\frac{4(+\infty)^3}{4(+\infty)}=\frac{+\infty}{+\infty} = \bm{+\infty}$

Bu durumda ∞/∞ belirsizliği +∞ verir çünkü payın derecesi paydanın derecesinden büyüktür.

Alıştırma 4

Aşağıdaki kesirli fonksiyonun limitini x 0’a yaklaşırken çözün:

$\displaystyle\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)$

Çözüme bakın

Öncelikle limiti her zamanki gibi hesaplamaya çalışıyoruz:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\frac{-3\cdot0-2}{0^4}-\frac{5}{0^2}=\frac{-2}{0}-\frac{5}{0}=\bm{\infty-\infty}$

Ancak ∞-∞ belirsiz formunu elde ederiz. Bu nedenle fonksiyonun kesirlerini ortak bir paydaya indirmemiz gerekiyor.

Bu durumda, x ⁴ , x ^2’nin bir katıdır, dolayısıyla ikinci kesirin pay ve paydasını x ² ile çarparak her iki kesrin de aynı paydaya sahip olduğunu elde edeceğiz:

$\begin{array}{l}\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5}{x^2}\right)=\\[5ex]\displaystyle =\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5\cdot x^2}{x^2\cdot x^2} \right)=\\[5ex]\displaystyle =\lim_{x\to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)\end{array}$

Artık iki kesri çıkarabiliriz:

$\displaystyle\lim_{x \to 0}\left(\frac{-3x-2}{x^4}-\frac{5x^2}{x^4}\right)=\lim_{x\to 0}\frac{-3x-2-5x^2 }{x^4}$

Limiti tekrar çözmeye çalışıyoruz:

$\displaystyle \lim_{x \to 0} \cfrac{-3x-2-5x^2 }{x^4} =\cfrac{-3\cdot 0-2-5\cdot 0^2}{0^4}=\frac{-2}{0}$

Ama sonunda bir sabitin sıfıra bölünmesinin belirsizliğiyle karşılaşırız. Bu nedenle fonksiyonun yanal sınırlarını hesaplamak gerekir.

$\displaystyle\lim_{x \to 0^{-}} \frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

$\displaystyle\lim_{x \to 0^{+}}\frac{-3x-2-5x^2}{x^4}=\frac{-2}{+0}=-\infty$

Sonuç olarak, fonksiyonun x=0 noktasındaki iki yanal limiti -∞ verdiğinden limitin çözümü -∞ olur:

$\displaystyle \lim_{x \to 0^-}f(x)=\lim_{x \to 0^+}f(x)=-\infty\ \longrightarrow \ \lim_{x \to 0}f(x)= \bm{-\infty}$

Alıştırma 5

Aşağıdaki fonksiyonun sonsuzluğa olan limitini köklerle çözün:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)$

Çözüme bakın

Limiti çözmeye çalışırken, sonsuz eksi sonsuz belirsizliğini elde ederiz:

$\displaystyle\lim_{x\to +\infty}\left(4x^2-\sqrt{x^4+1}\right)=4(+\infty)^2-\sqrt{(+\infty)^4}=\bm{+\infty -\infty}$

Bu nedenle, fonksiyonda radikaller olduğundan, onu eşlenik radikal ifadeyle çarpmamız ve bölmemiz gerekir:

$\displaystyle\lim_{x \to +\infty}\left(4x^2-\sqrt{x^4+1} \right)=\lim_{x \to +\infty}\frac{\left(4x^2-\sqrt{x^4+1}\right)\cdot\left(4x^2+\sqrt{x^4+1}\right)}{4x^2+\sqrt{x^4+1}}$

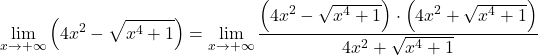
Payda, kareler farkına eşit olan bir fark toplamının kayda değer çarpımına sahibiz. Henüz:

$\displaystyle\lim_{x\to +\infty}\frac{\left(4x^2\right)^2-\left(\sqrt{x^4+1}\right)^2}{4x^2+\sqrt{x^4+1}}$

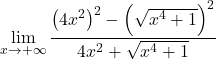
Radikalleri kareye sadeleştiriyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{\bigl(4x^2\bigr)^2-(x^4+1)}{4x^2+\sqrt{x^4+1}}$

Payda çalışıyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{16x^4-x^4-1}{4x^2+\sqrt{x^4+1}}$

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}$

Ve son olarak limiti buluyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{15x^4-1}{4x^2+\sqrt{x^4+1}}=\frac{15(+\infty)^4}{4(+\infty)^2+\sqrt{(+\infty)^4}}=\frac{+\infty}{+\infty}= \bm{+\infty}$

Bu durumda sonsuz belirsizliğin sonsuza bölümü daha sonsuzdur çünkü payın derecesi paydanın derecesinden büyüktür (karekökün dereceyi iki oranında azalttığını hatırlayın:

$\sqrt{x^4} = x^{4/2} = x^2$

Alıştırma 6

Aşağıdaki irrasyonel fonksiyonun x sonsuza yaklaşırken limitini çözün:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)$

Çözüme bakın

Öncelikle limiti her zamanki gibi hesaplamaya çalışıyoruz:

$\displaystyle\lim_{x\to +\infty}\left(2x-1-\sqrt{4x^2+1}\right)=2(+\infty)-\sqrt{4(+\infty)^2}=\bm{+\infty -\infty}$

Ama sonuç olarak bize sonsuzluklar farkının belirsizliğini verir. Bu nedenle, fonksiyonun kökleri olduğundan, ifadeyi eşlenik radikalle çarpmamız ve bölmemiz gerekir:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1-\sqrt{4x^2+1}\right)\cdot\left(2x-1+\sqrt{4x^2+1}\right)}{2x-1 +\sqrt{4x^2+1}}$

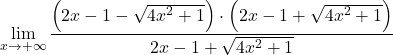
Kesir payının dikkate değer eşitliğini gruplandırıyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(\sqrt{4x^2+1}\right)^2}{2x-1+\sqrt{4x^2+1}}$

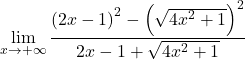
Karekökü çözüyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{\left(2x-1\right)^2-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

Bir farkın karesinin dikkate değer kimliğini çözüyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-\left(4x^2+1\right)}{2x-1+\sqrt{4x^2+1}}$

Payda çalışıyoruz:

$\displaystyle\lim_{x\to +\infty}\frac{4x^2+1-4x-4x^2-1}{2x-1+\sqrt{4x^2+1}}$

$\displaystyle\lim_{x \to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1}}$

Ve son olarak sonsuzdaki limitin değerini hesaplıyoruz:

$\displaystyle\lim_{x \to +\infty} \cfrac{-4x }{2x-1 +\sqrt{4x^2+1} } = \cfrac{-4(+\infty) }{2(+\infty)+\sqrt{4(+\infty)^2} } = \cfrac{-\infty}{+\infty} =$

Paydada x kare olsa da bir kökün içinde olduğu için derecesi aslında 1’dir:

$\sqrt{4x^2} =\sqrt{4}\cdot \sqrt{x^2} = \sqrt{4}\cdot x^{2/2} =\sqrt{4} x^1=\sqrt{4}x .$

Bu nedenle, -∞/+∞ belirsizliğinin sonucu, payın derecesi paydanın derecesi ile aynı olduğundan, daha yüksek dereceli x’in katsayılarının bölümüdür.

$\displaystyle\lim_{x\to +\infty}\frac{-4x}{2x-1+\sqrt{4x^2+1} }=\frac{-\infty}{+\infty}=\frac{-4}{2+\sqrt{4}}=\frac{-4}{2+2}=\frac{-4}{4}=\bm{-1}$

Paydada birinci dereceden iki terim olduğundan

$\bigl(2x$

$\sqrt{4x^2}\bigr)$

-∞/+∞ belirsizliğini çözmek için birinci dereceden terimlerin tüm katsayılarını almak gerekir, yani

$2$

ile ilgili

$2x$

$\sqrt{4}$

ile ilgili

$\sqrt{4x^2}.$

Egzersiz 7

Aşağıdaki kesirli fonksiyonun x’i 1’e yaklaşırken limitini hesaplayın:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)$

çözümü gör

Limiti yapmaya çalışırken sonsuzluğun belirsiz limiti eksi sonsuzu elde ederiz:

$\displaystyle\lim_{x\to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3}\right)=\frac{1}{1-1}--\frac{3}{1-1^3}=\frac{1}{0}-\frac{3}{0}=\bm{\infty-\infty}$

Bu nedenle kesirleri ortak bir paydaya indirmeliyiz, yani bir kesrin payını ve paydasını diğerinin paydasıyla çarpmamız gerekir:

$\begin{array}{l}\displaystyle\lim_{x \to 1}\left(\frac{1}{1-x}-\frac{3}{1-x^3} \right)=\\[5ex]\displaystyle =\lim_{x\to 1}\left( \frac{1\cdot(1-x^3)}{(1-x)\cdot(1-x^3)}-\frac{3\cdot(1-x)}{(1-x^3)\cdot(1-x)}\right)=\\[5ex]\displaystyle =\lim_{x \to 1}\left(\frac{1-x^3}{1-x-x^3+x^4}-\frac{3-3x}{1-x-x^3+x^4}\right)\end{array}$