Basit faiz , faiz hesaplamanın en yaygın yoludur ve ev satın almaktan bireysel kredi almaya kadar çeşitli amaçlar için kullanılır. Basit faizi hesaplamanız gerekirse, bu kılavuz size bunu nasıl adım adım yapacağınızı gösterecektir. Görevinizi kolaylaştırmak için size çevrimiçi bir hesap makinesi de sunuyoruz.
Basit Faiz Hesaplayıcı
Bu çevrimiçi basit faiz hesaplayıcı, basit faiz hesaplamasında yer alan değişkenlerden herhangi birini hesaplamanıza yardımcı olabilecek bir araçtır. Bunu kullanmak için neyi hesaplamak istediğinizi seçin ve istediği değişkenlere ilişkin verileri girin. Daha sonra hesapla butonuna tıklamanız gerekiyor ve bu kadar.
Basit faiz nedir?
Basit faiz, belirli bir süre boyunca bir miktar yatırım yaptığınızda veya borç verdiğinizde uygulanan faiz oranıdır. Başlangıç tutarının faiz oranı ve zamanla çarpılmasıyla hesaplanır. Özetle bu faiz, sürekli ve normalde kısa vadeli finansal işlemlerde kullanılmaktadır.
Faiz oranı ve vade sabit tutulduğu için faiz artmadığı için aylık veya yıllık ödenmesi gereken faiz her zaman aynıdır . Basit faiz ile bileşik faiz arasındaki temel fark budur.
Aşağıdaki resimde yeşil renkte basit faizi temsil eden fonksiyonu ve mavi renkte gösterilen bileşik faiz fonksiyonunu görebilirsiniz. Görselde de görebileceğimiz gibi çok daha üstel bir şekle sahip.
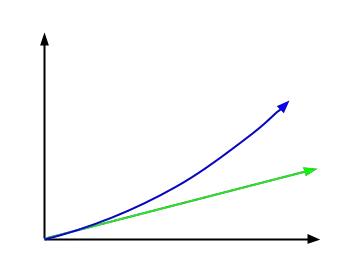
Basit faiz hesaplama formülü
Basit faizi hesaplama formülü şöyledir: I = C xixt , burada aşağıdaki değişkenler devreye girer:
- Başlangıç sermayesi (C): Basit faizin hesaplandığı, yatırılan veya borç verilen paranın toplamı.
- Faiz oranı (i): Bu gösterge bize faiz miktarının zamana göre yüzdesini verir. Formülde birer birer yazmak (yüzde değerini yüze bölmek) önemlidir.
- Süre (t): Genellikle yıl olarak ifade edilen yatırım süresinin uzunluğu. Ancak aşağıda size bunu aylar ve günler gibi diğer zaman birimlerine nasıl dönüştüreceğinizi öğreteceğiz.
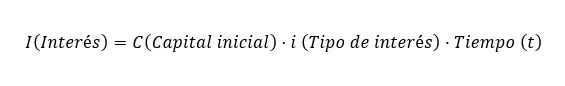
Bu formülün nasıl kullanıldığını görmek için şu örneği inceleyebiliriz: Yıllık %4 oranında 1000 € yatırım yaptık, üç yıl sonra ne kadar faiz üreteceğiz? Yaratılan ilgiyi bulmak için şu formülü uygulamalıyız: I = C x (i ÷ 100) xt = 1000 x (4 ÷ 100) x 3 = 120 €.
Daha sonra ana formülden farklı değişkenleri izole edebiliriz ve böylece başlangıç sermayesini, faiz oranını, zamanı ve nihai sermayeyi hesaplamamızı sağlayan formülleri elde ederiz. Ve bunu, daha önce gördüğünüz ve çok basit bir formülden yararlanarak bu değişkenleri nasıl hesaplayacağınızı size öğreteceğimiz sonraki bölümlerde göreceğiz.
Nihai sermaye nasıl hesaplanır?
Nihai sermayeyi hesaplamak için mantığı uygulamanız yeterlidir. Daha sonra nihai tutar başlangıç tutarına eşit olduğundan faizi uyguladığımızda formülü şu şekilde olur: Nihai sermaye (Cf) = Başlangıç sermayesi (C) + Faiz (I). Bu ifade ikinci en önemli basit faiz formülü olup en önemlisi bir öncekidir.
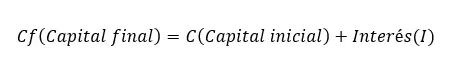
Artık formülü bildiğinize göre şu pratik örneği çözmeye çalışın: 4 yıllığına 50.000 € yatırım yaparsanız, 20.000 € faizle elde edeceğiniz nihai sermaye nedir? Basitçe, önceki ifadeyi uyguluyoruz: Nihai sermaye (Cf) = Başlangıç sermayesi (C) + Faiz (I) = 50.000 + 20.000 = 70.000 €.
Başlangıç sermayesi nasıl hesaplanır?
Başlangıç sermayesini hesaplamak istersek bize verdikleri verilere göre iki formül kullanabiliriz. Öncelikle elimizde nihai sermaye ve faizin oluşturduğu tutar varsa önceki bölümdeki ifadeyi uygulayabiliriz: Başlangıç sermayesi (C) = Nihai sermaye (Cf) – Faiz (I).
İkincisi, başlangıç sermayesinin değerini (başlangıçta bahsettiğimiz) basit faiz formülüne ayırabiliriz. Bu nedenle Başlangıç sermayesi (C) = Faiz (I) ÷ (Zaman (t) x Faiz oranı (i)) ile kalırız.

İkinci, daha karmaşık duruma bir örnek verelim: 2 yıl boyunca %8 faiz oranıyla 30.000 €’ya faiz elde etmek için ne kadar yatırım yapmalıyım? Başlangıç sermayesi = I ÷ (tx (i ÷ 100)) formülünü uyguluyoruz, bu da bize başlangıç için 30.000 ÷ (2 x (8 ÷ 100)) = 187.500 € bırakıyor.
Faiz oranı nasıl hesaplanır?
Faiz oranını hesaplamak için basit faiz formülünü de kullanmamız gerekir, ancak i’yi yalnız bırakmamız gerekir. Dolayısıyla elimizde şu kalıyor: Faiz Oranı (i) = Faiz (I) ÷ (Başlangıç Sermayesi (C) x Zaman (t)). Gördüğünüz gibi tüm formüller aynı ancak farklı bir değişkeni izole ediyorlar.
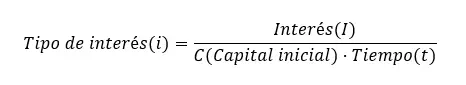
İşte faiz oranlarını hesaplamanın pratik bir örneği: Eğer 200.000 €’ya dönüştürmek istiyorsak, 5 yıl boyunca hangi faiz oranıyla 180.000 € yatırım yapmalıyız? Bu örnekte öncelikle faizi bulmalısınız: I = Cf – C = 200.000 – 180.000 = 20.000 €. Ve sonra çözüyoruz: Faiz oranı = 20.000 ÷ (180.000 x 5) = 0,022 x 100 = %2,2.
Zaman nasıl hesaplanır?
Son olarak, başlangıç formülünden de elde edilebilecek zamanı hesaplayabiliriz: Zaman (t) = Faiz (I) ÷ (Başlangıç tutarı (C) x Faiz oranı (i)). Formülün zaman birimlerinin yıl olmasını gerektirdiğini unutmamak önemlidir. Ancak bunu başka birimlerle ifade etmek istiyorsanız formülün aşağıdaki varyasyonlarını kullanabilirsiniz:
- I = C · (i / 100) · t eğer t yıl ise (Genel Formül)
- I = C · (i / 1200) · t eğer t ay ise (Sonuç ay olarak)
- I = C · (i / 36000) · t eğer t gün ise (Sonuç gün olarak)
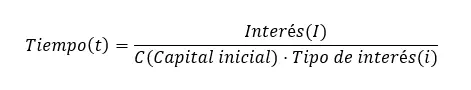
Şu örneğe bakın: Eğer 40.000€’luk bir yatırımın %5’lik bir oranla 5.000€ faiz getirmesini istiyorsak ne kadar zaman geçmesi gerekir? Hesaplama şu şekilde kalır: Zaman = 5.000 ÷ (40.000 x 5 ÷ 100) = 2,5 yıl. Ancak ay cinsinden hesaplamak istersek şunu yapabiliriz: Zaman = 5.000 ÷ (40.000 x 5 ÷ 1200) = 30 ay.
Basit Faiz Hesaplamasının Gerçek Hayat Örneği
Artık basit faiz formülünü oluşturan her değişkenin hesaplanmasına ilişkin bir örnek gördünüz. Ancak, size en yaygın hesaplamanın son bir örneğini göstermek istiyoruz ki o da ilgi çekici olanın kendisidir. İlk formülü uygulayacağınız artıklara sahip olacaksınız. Hesaplamayı gözden geçirmek isterseniz işte bir örnek olay:
Yatırım yapmak için 10.000 € borç alıyoruz ve bizden yıllık %3 faiz isterlerse 5 yıl sonra ne kadar para geri ödememiz gerektiğini hesaplamak istiyoruz. Hesaplama şöyle olacaktır:
10.000 x 0,03 = 300
300 x 5 yıl = 1.500 €
CF = 10.000 € + 1.500 € = 11.500 €
Böylece 5 yılın sonunda faiz 1.500€, ödenecek nihai sermaye ise 11.500€ olacaktır .
çözüm
Özetle basit faiz hesaplamak için kredi tutarını, faiz oranını ve süresini dikkate almanız gerekir. Buradan ödenecek toplam faiz tutarını bulmak için bu üç sayıyı çarpmanız yeterlidir. Ve faiz yerine diğer değişkenlerden birini hesaplamak istiyorsanız, genel formülde bu değeri ayırmanız yeterlidir.