Bu yazımızda bir fonksiyonun monotonluğunun nasıl bilineceğini, yani bir fonksiyonun artış ve azalış aralıklarının nasıl bulunacağını açıklıyoruz. Ayrıca bir fonksiyonun büyümesi ve azalmasıyla ilgili adım adım alıştırmalarla pratik yapabilirsiniz.
Bir fonksiyonun monotonluğu nedir?
Bir fonksiyon belirli bir aralıkta verilen sırayı koruyorsa monotondur. Beş tür monotonluk vardır:
- Monoton artan fonksiyon: Fonksiyonun bir noktadaki değerinin her zaman bir önceki noktadaki değerine eşit veya ondan büyük olması.
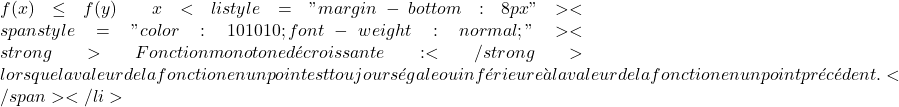Kesinlikle monoton artan fonksiyon: Fonksiyonun bir noktadaki değeri, fonksiyonun bir önceki noktadaki değerinden her zaman büyük olduğunda.
Fonksiyonun bir noktadaki değeri her zaman bir önceki noktadaki değerine eşit olduğunda sabit fonksiyon .
x^2-4=0x^2=4x=\pm 2
\text{Dom } f= \mathbb{R}-\{+2, -2 \}
f(x)=\cfrac{3}{x^2-4} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-4) – 3\cdot 2x}{\left( x^2-4\right)^2}f'(x)=\cfrac{-6x}{\left(x^2-4\right)^2}
f'(x)=0\cfrac{-6x}{\left(x^2-4\right)^2}=0
\left(x^2-4\right)^2}
-6x=0\cdot \left(x^2-4\right)^2-6x=0x=\cfrac{0}{-6}x=0
f'(x)=0,
(-\infty,0)
f'(x)=0.
f(x)=x^3-6x^2+9x \ \longrightarrow \ f'(x)=3x^2-12x+9
f'(x)= 03x^2-12x+9=0\begin{aligned}x &=\cfrac{-b \pm \sqrt{b^2-4ac}}{2a} = \cfrac{-(- 12) \pm \sqrt{(-12)^2-4\cdot 3 \cdot 9}}{2\cdot 3}=\\[2ex]&= \cfrac{+12 \pm \sqrt{144-108 }}{6} =\cfrac{12 \pm 6}{6}=\begin{vakalar} \cfrac{12 + 6}{6}= 3 \\[4ex] \cfrac{12 – 6}{6} =1 \end{durumlar} \end{aligned}
f'(x)=0
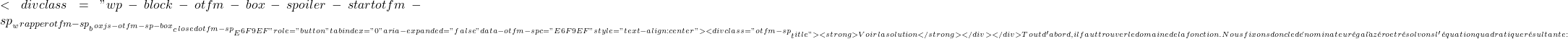
\text{Dom } f= \mathbb{R}-\{+3, -3 \}
f(x)=\cfrac{5}{x^2-9} \ \longrightarrow \ f'(x)= \cfrac{0\cdot (x^2-9) – 5\cdot (2x)}{\ left(x^2-9\right)^2}f'(x)= \cfrac{-10x}{\left(x^2-9\right)^2}
f'(x)= 0\cfrac{-10x}{\left(x^2-9\right)^2}=0 -10x=0\cdot \left(x^2-9\right)^2 – 10x= 0 x= \cfrac{0}{-10} x=0
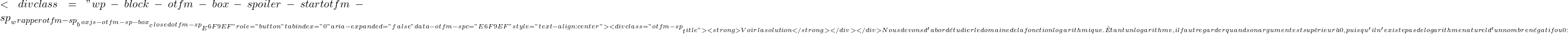
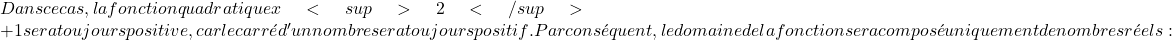
f(x)=\ln \bigl(x^2+1 \bigr) \ \longrightarrow \ f'(x)=\cfrac{1}{x^2+1 } \cdot (2x)f'(x) = \cfrac{2x}{x^2+1}
f'(x)= 0\cfrac{2x}{x^2+1}=0 2x=0\cdot \left(x^2+1\right) 2x= 0 x= \cfrac{0}{2} x=0
